根式代数式化简方法归纳
1、含有√a,且a为整数的化简,思路是将a中含有能开方的因数提出。
2、√180,180含有最大的能开发的因数是36.
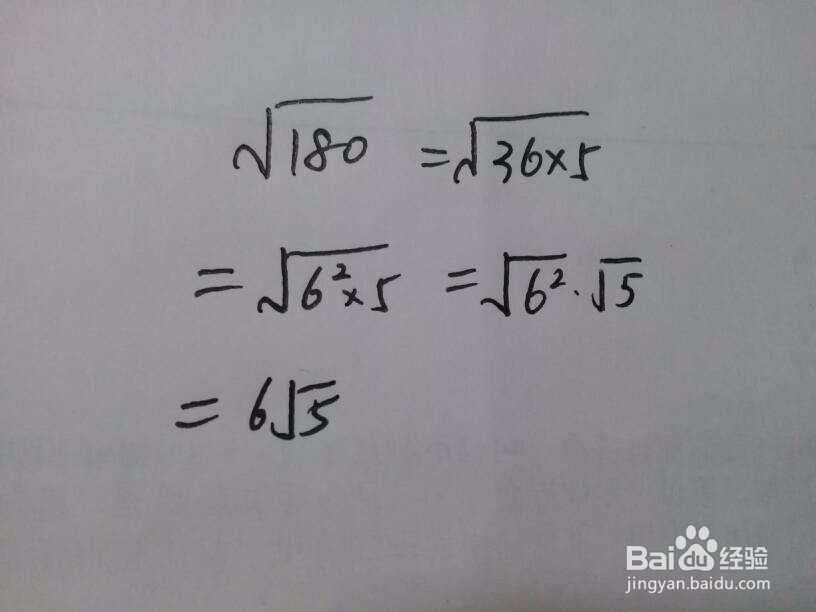
3、√3100,√2400,能提出100=10^2

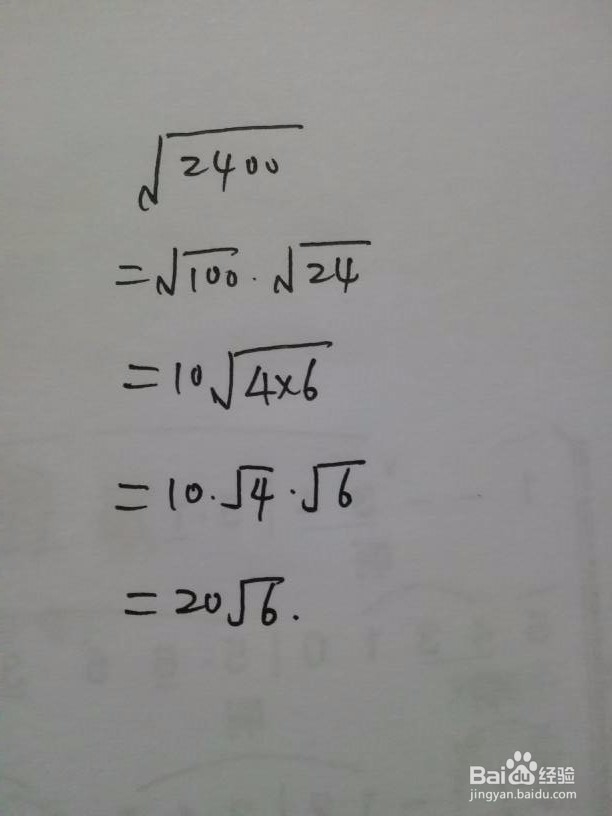
4、√363,能提出121=11^2.
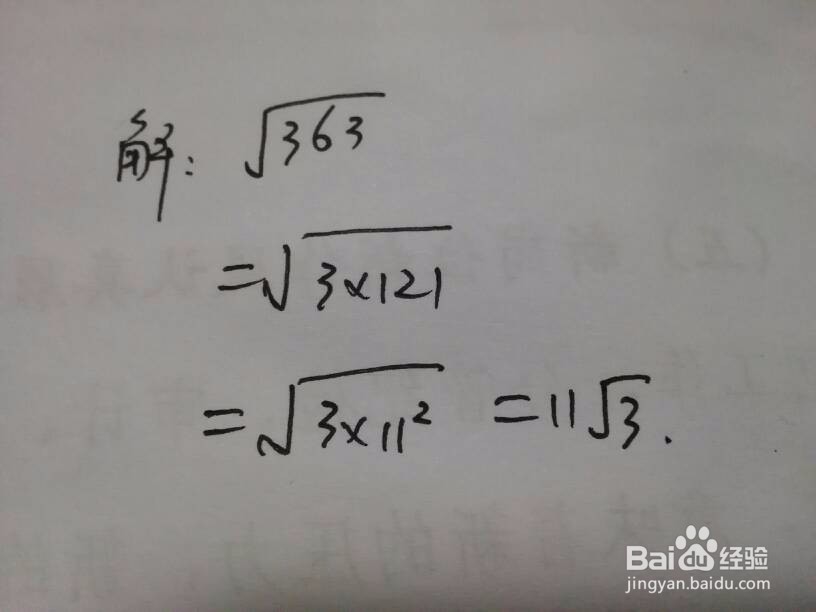
5、√156,能提出4=2^2.
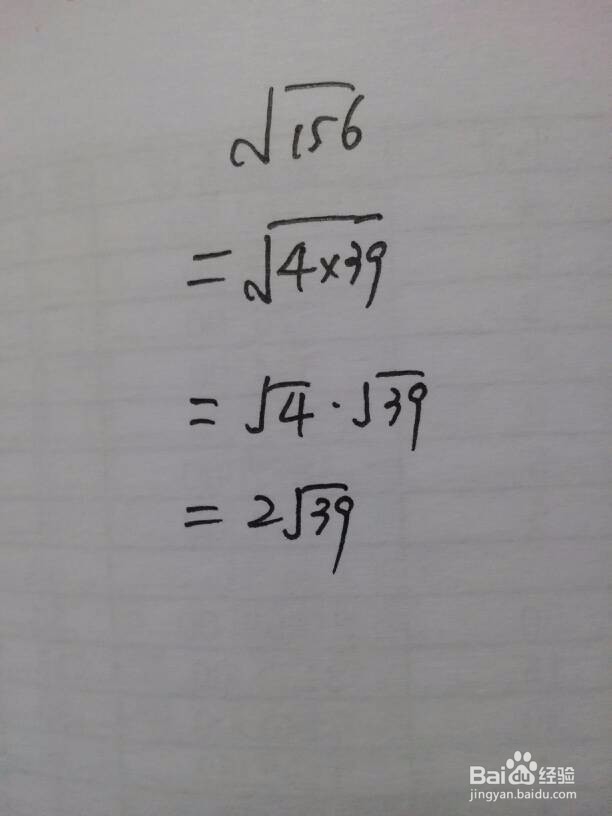
6、以下为几种分数、分式类型的化简。
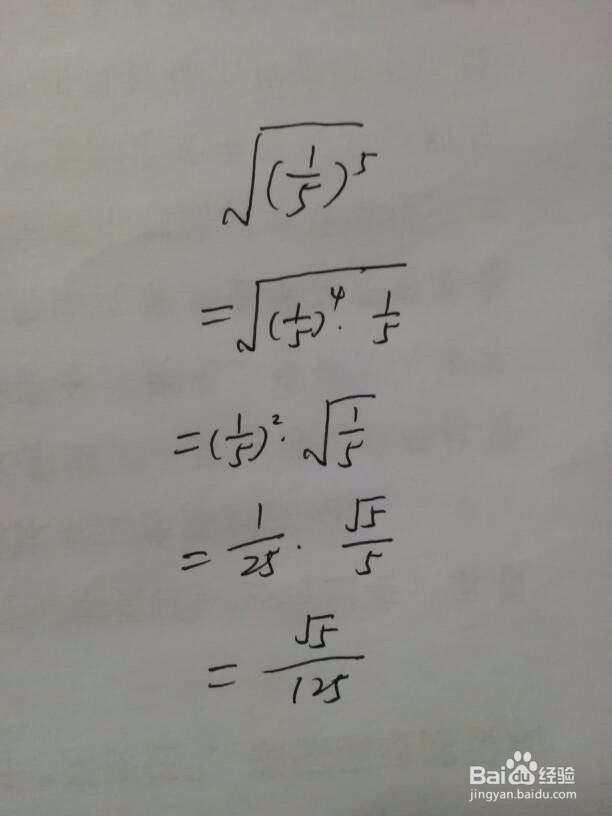

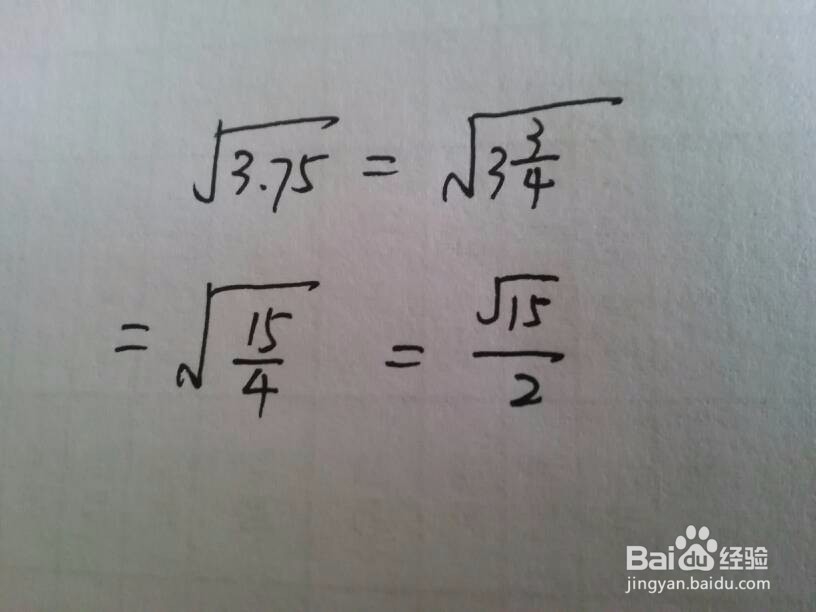
1、|-a|=a,当a>=0时候成立。
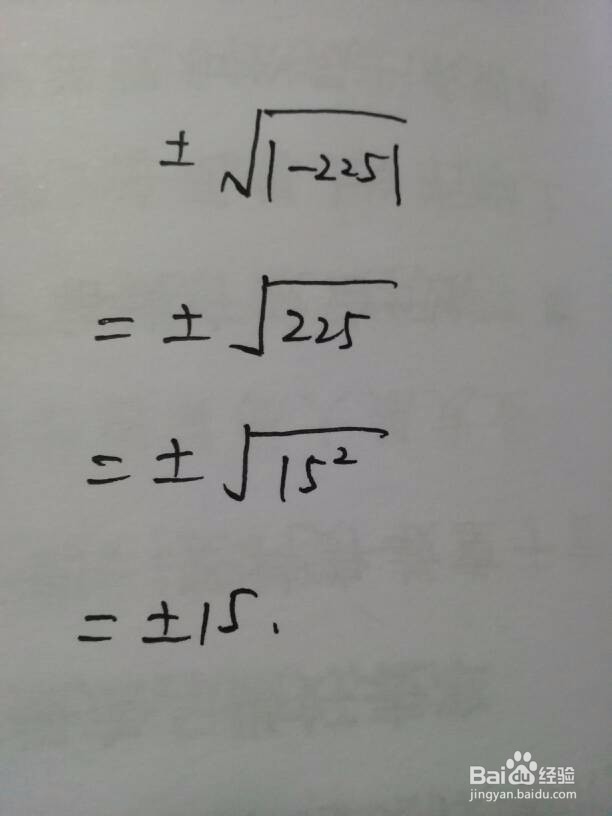
2、(-a)^2=|-a|^2=a^2,当负号在平方里边的类型。
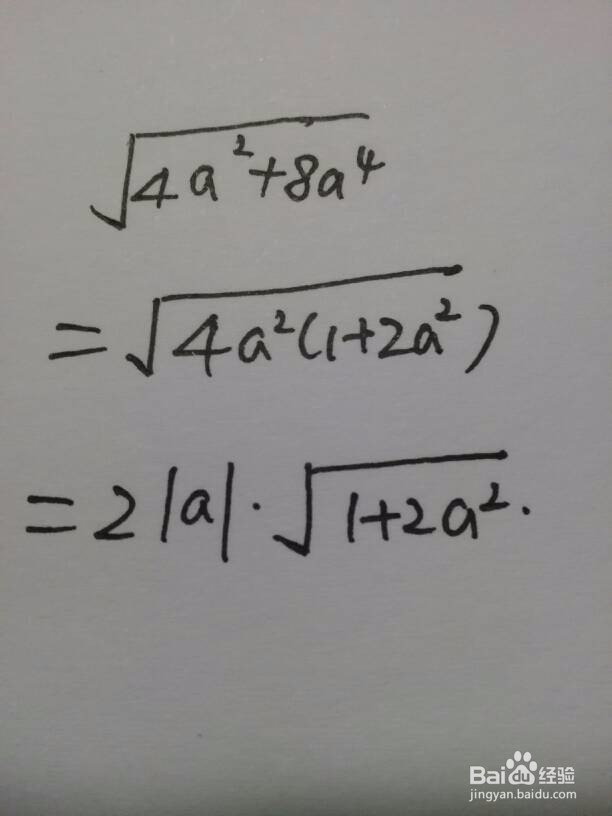
3、a^2为非负数,但a可正、可负,也可以为0,所以开方需取绝对值。
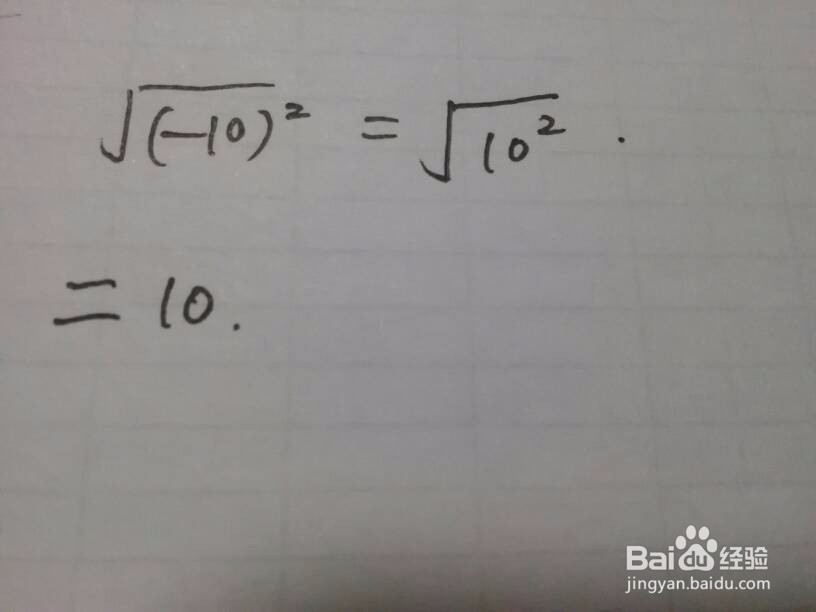
4、三角函数根式的开方,需取绝对值。
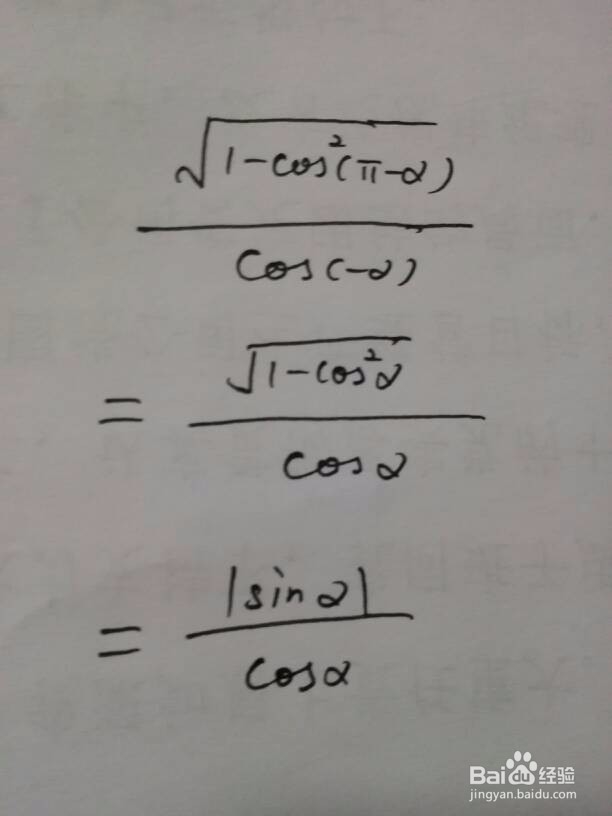
1、两项或多项含有可开发因子的乘积形式。
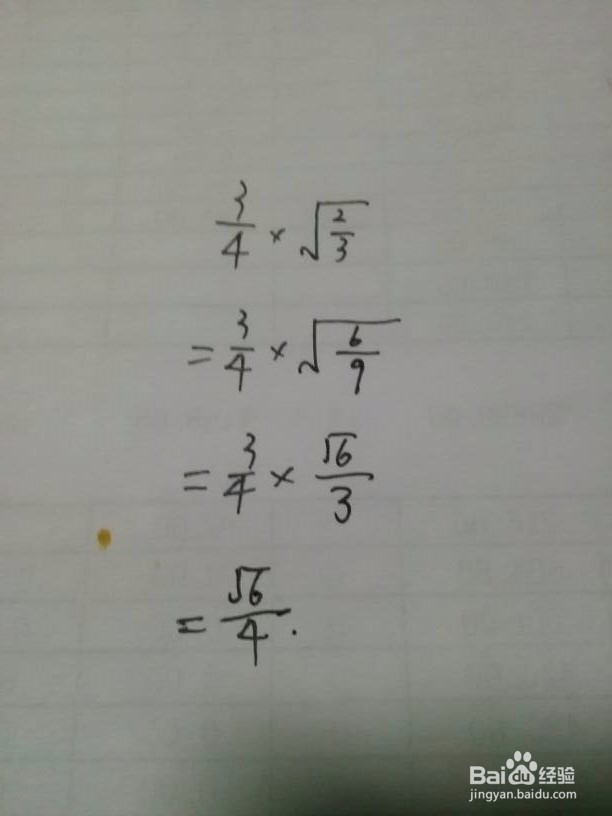

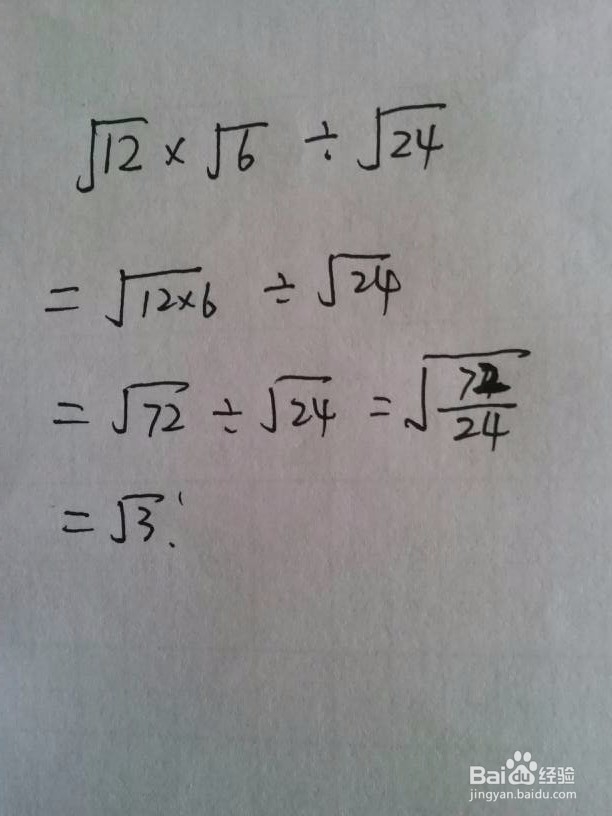
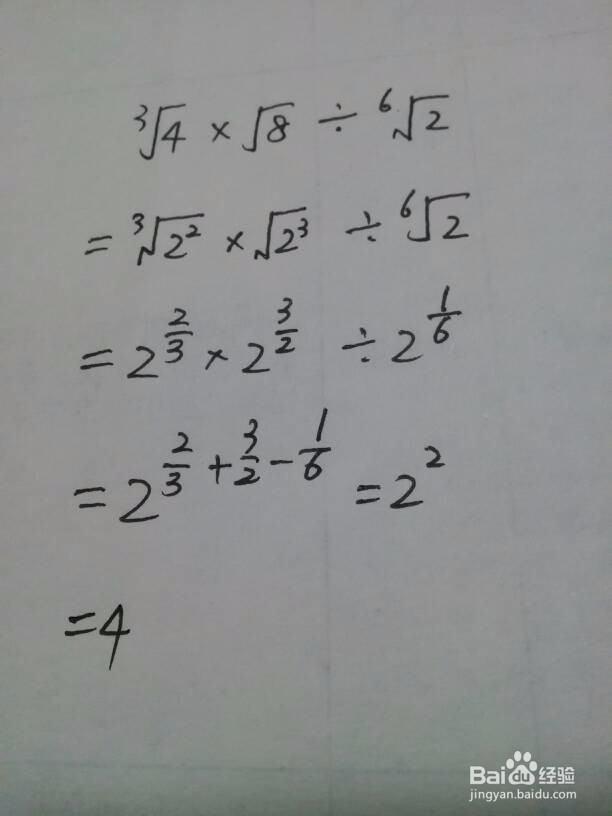
2、多项式和差类型的化简

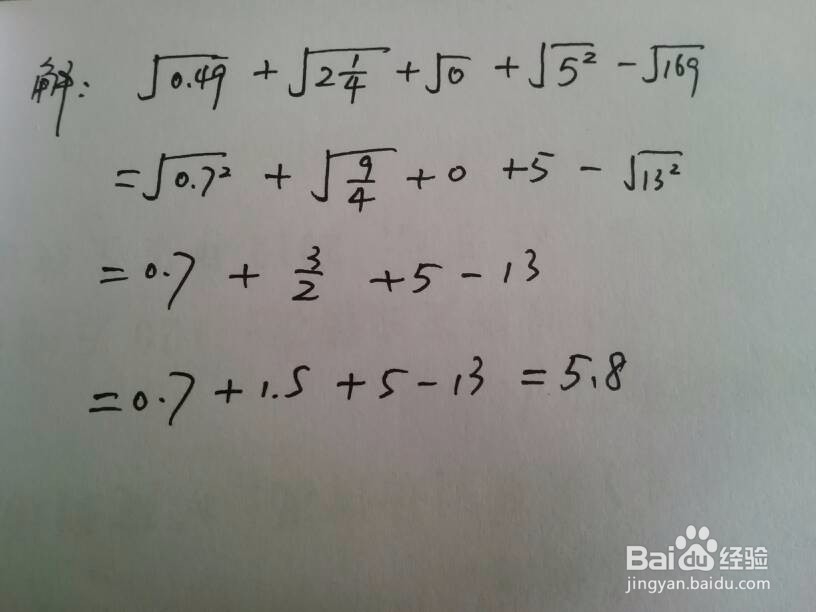
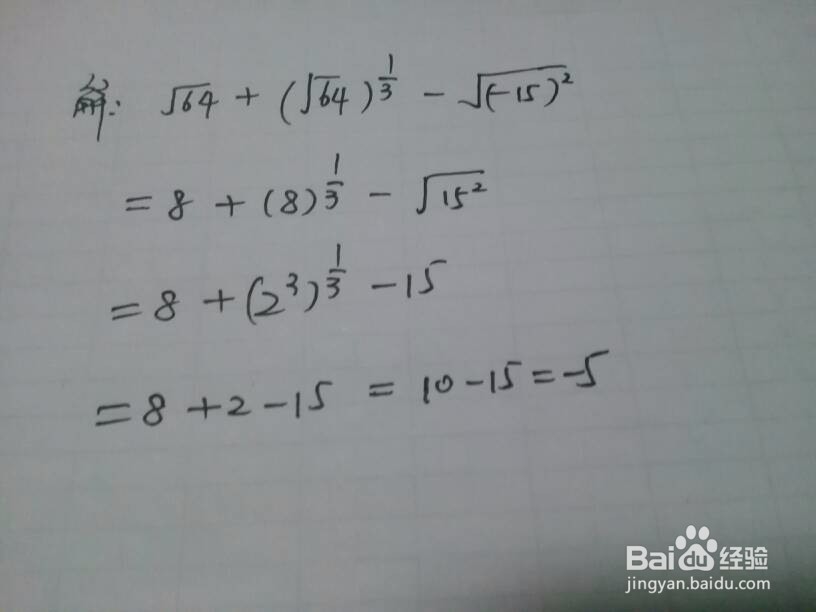

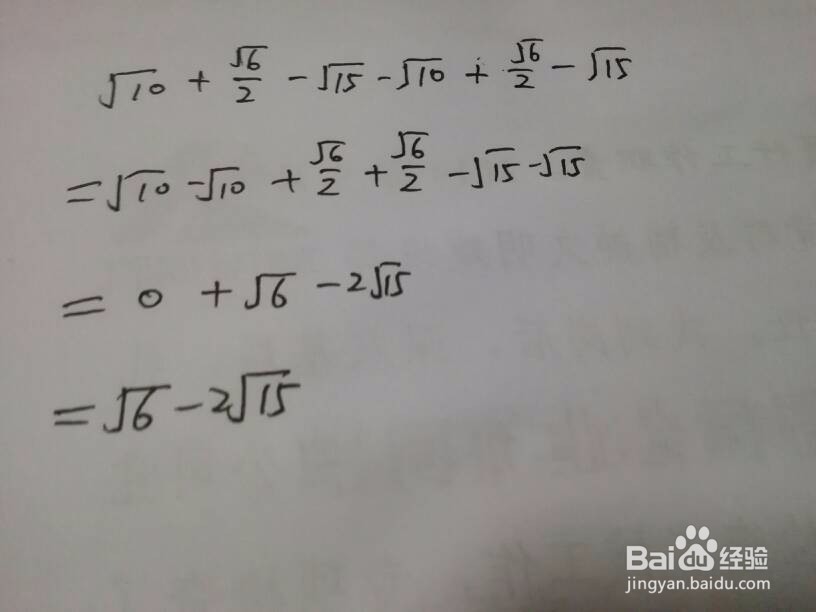
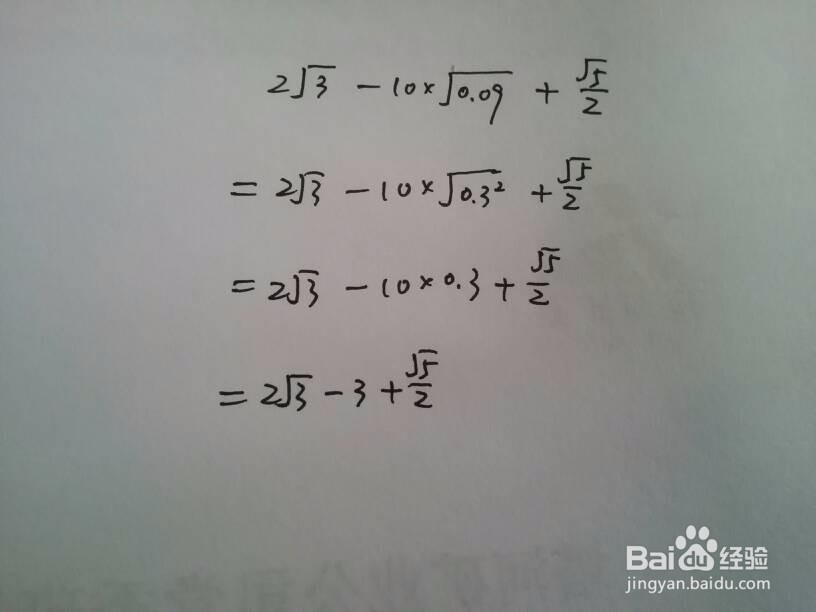
3、含有立方及开立方类型。
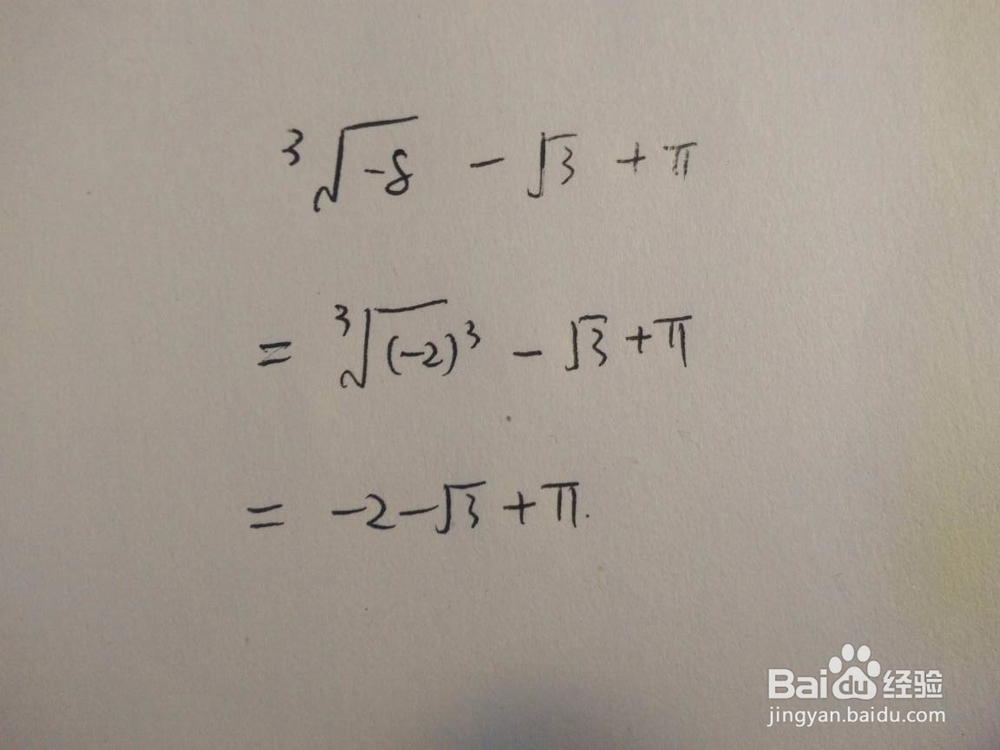
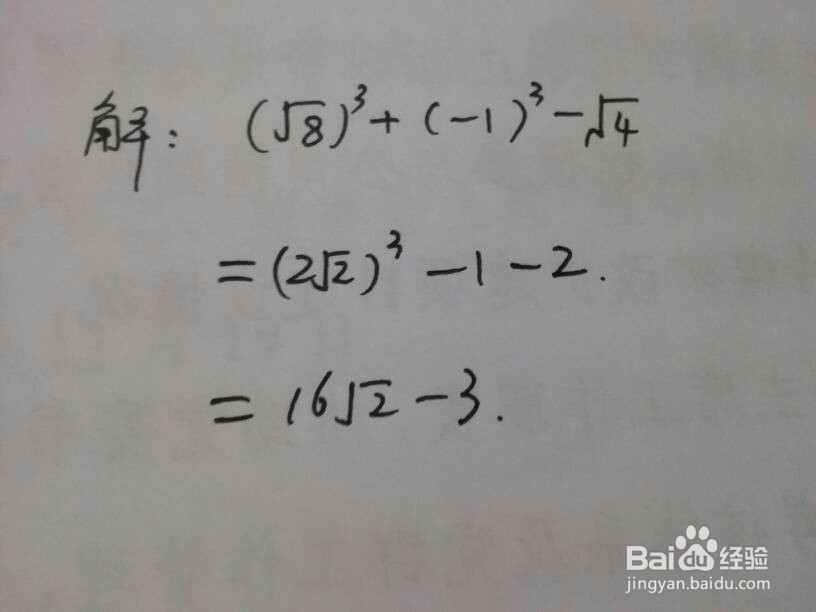
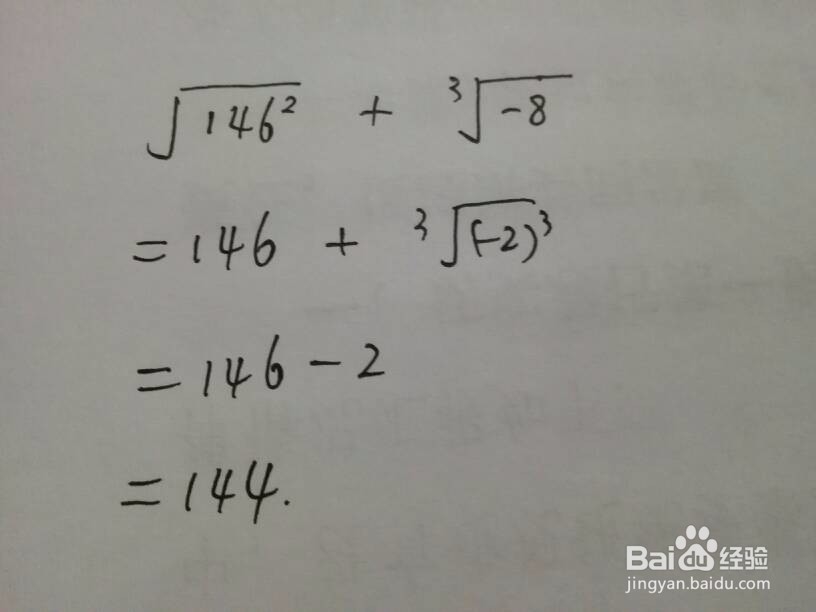
4、含有绝对值类型的步骤。

1、两个不同根式的比较,方法是通分,使其分母保持一致,比较分子大小。

2、两个不同式子的比较,还可以通过相减的差与0的关系来进行比较。
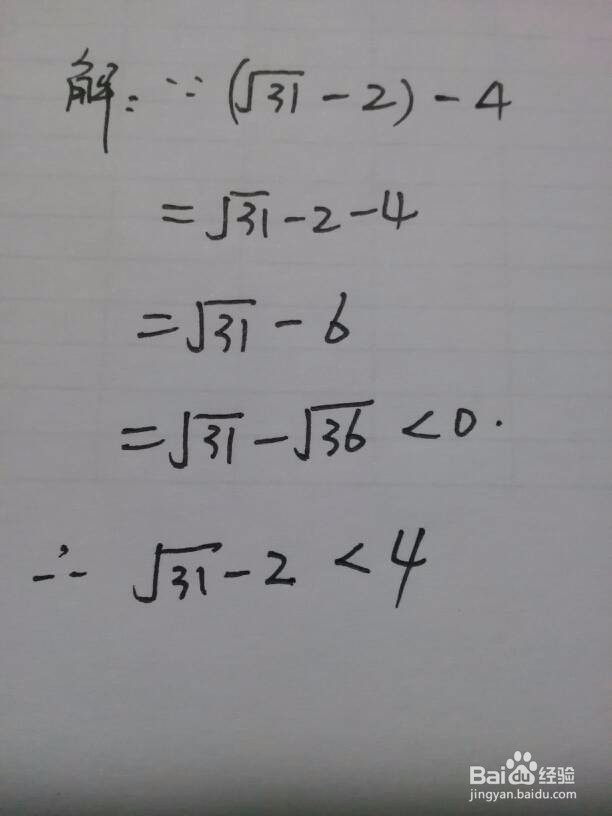
1、3+√5/2作为根式内部,需分子分母同乘以2而可进行开方计算。
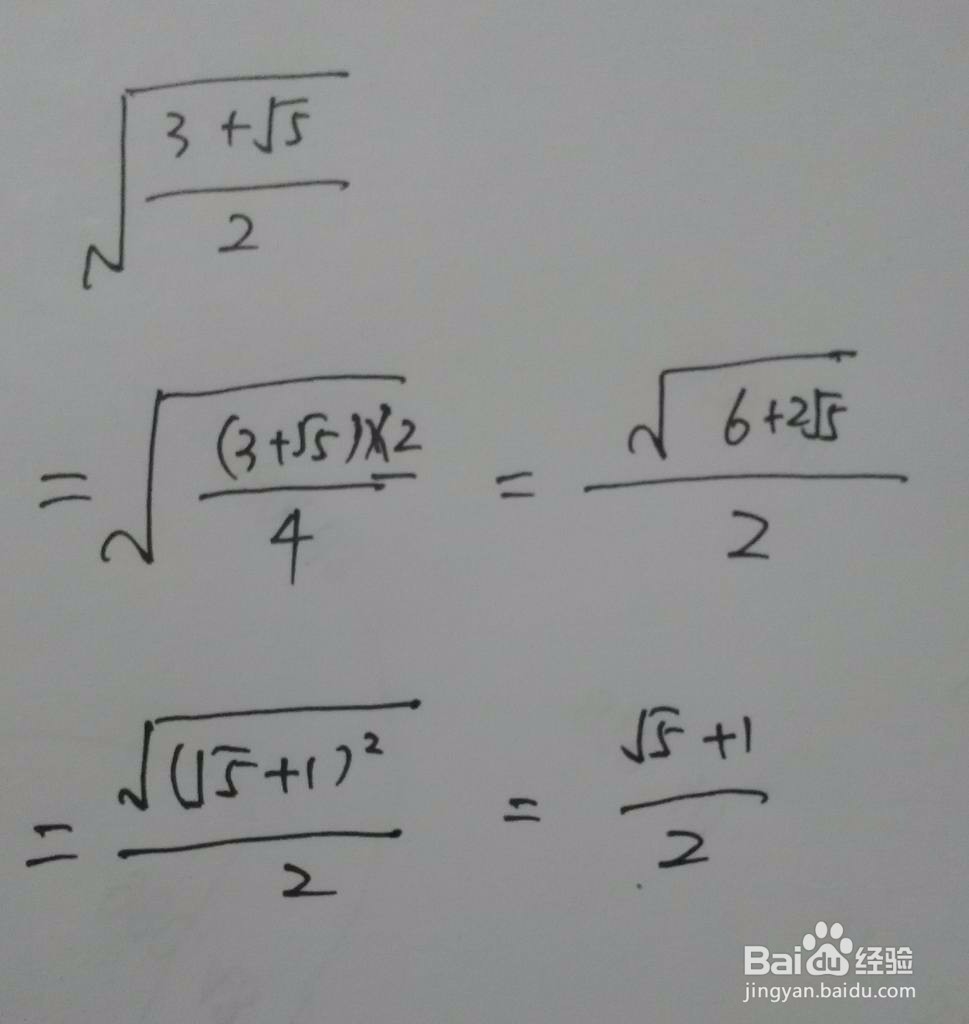
2、含有√6+√2的情形。

3
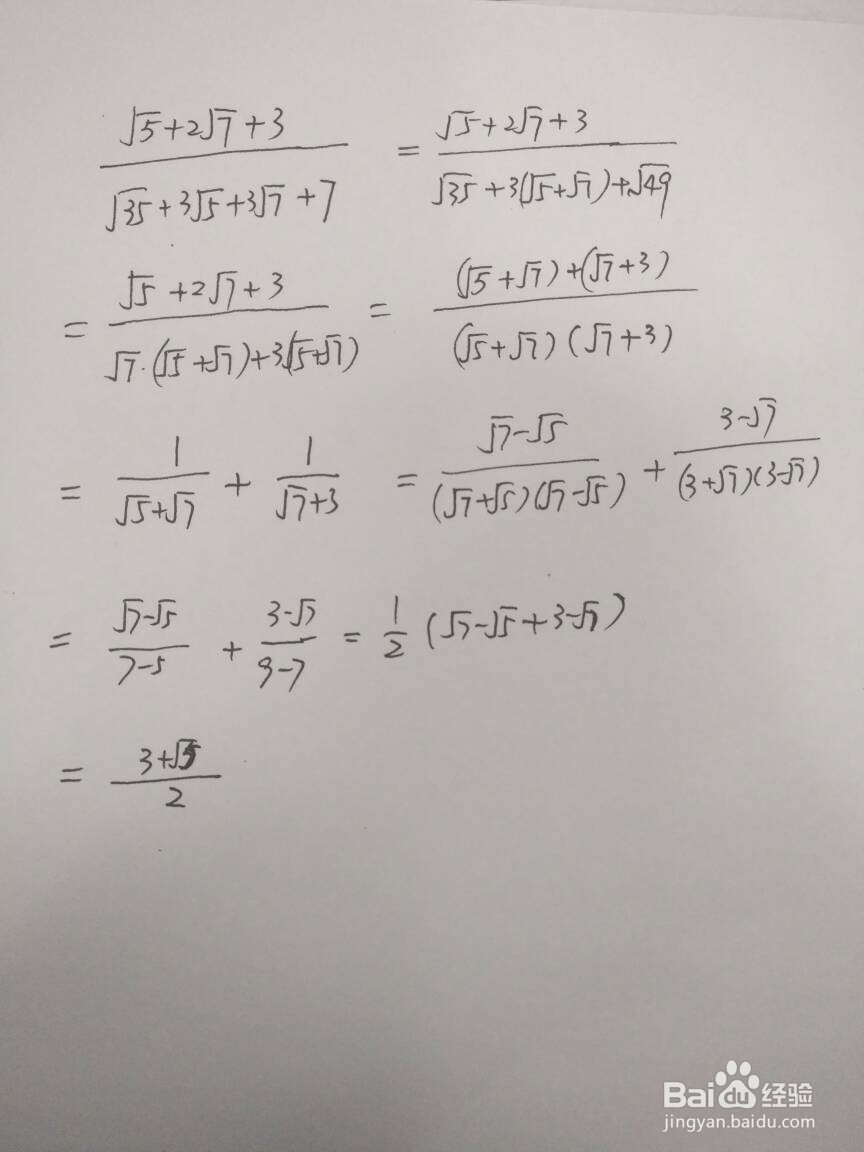
1、对分母为两个根式的和或差,多半采用分母有理化的方法求解。
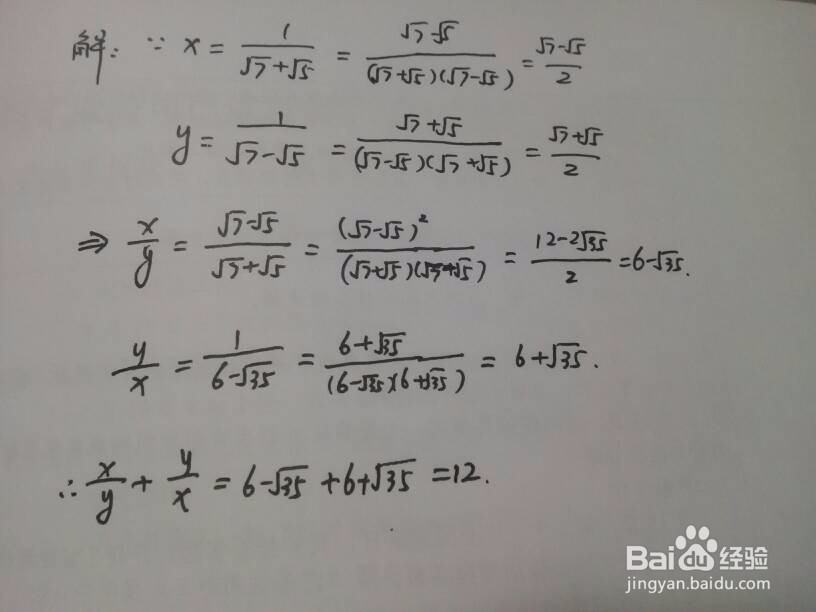
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。