【抽象代数】Mathematica怎么输出三对角矩阵？

1、先给出一个9阶单位矩阵：

A = IdentityMatrix[9];

2、把第一行的第二个元素置为1，

把第二行的第三个元素置为1，

……

以此类推，直到把第八行的第九个置为1。

这个过程，可以用Mathematica直接表示为：

(A[[#, # + 1]] = 1) & /@ Range[8];

最后一行（第九行）不作处理。

3、对每一列作类似的处理：

(A[[# + 1, #]] = 1) & /@ Range[8];

最后一列不作处理，这样就得到了九阶三对角矩阵。

4、打包成自定义函数，给出其它阶的三对角矩阵：

sanduijiao[n_] := Module[{A}, A = IdentityMatrix[n];

  (A[[#, # + 1]] = 1) & /@ Range[n - 1];

  (A[[# + 1, #]] = 1) & /@ Range[n - 1];

  A]

这个函数返回一个n阶三对角矩阵，前提是，n必须为具体的正整数。

5、测试一下：

MatrixForm[sanduijiao[16]]

6、MatrixForm[sanduijiao[#]] & /@ Range[5]

返回前五个三对角矩阵。

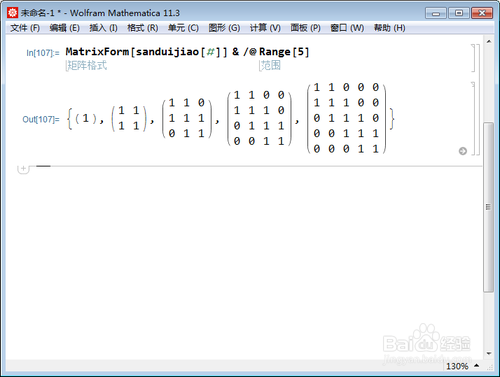
7、n必须为给定的具体正整数，对于未知数，运行会报错：

8、作为一个简单的应用，考察一下不同的三对角矩阵的行列式：

Det[sanduijiao[#]] & /@ Range[100]

可以发现，随着阶数的逐步增加，三对角矩阵的行列式呈现【周期性】，这个周期为6。