椭圆的作图问题——给定五个限定条件

1、        给定一个凸五边形ABCDE，作椭圆，使之经过五边形的五个顶点。具体步骤如下：

        设直线CE和BD交于P；

        以点B为圆心作任意圆，取圆的动点X，作直线BX；

        设直线AE和BX交于R；

        连接直线PR，与直线AD交于Q；

        连接直线CQ，与直线BX交于F；

        选中X、F，那么F的轨迹就是所求作的椭圆。

2、        作椭圆，使之与给定的凸五边形ABCDE的五边相切。具体步骤如下：

        设直线BD和直线ＡＣ交于Ｆ；

        连接直线ＥＦ，与直线ＢＣ交于Ｇ；

        那么，点Ｇ就是内切椭圆与五边形在BC上的切点；

        用同样的方法，可以确定这个椭圆与五边形的所有切点G、H、I、J、K；

        于是，这个问题就转化为过五个点作椭圆的情形。

3、        三角形JIH内部有定点G，直线JG、IG、HG分别与对应边交于M、L、K。

        求作椭圆，使之与三角形JIH的三条边切于M、L、K。

        彭老师给出的作图步骤：

        连结直线ML、MK；

        过点A作直线ML、MK的平行线，与直线HI交于N、O；

        以H为圆心、线段HN为半径作圆H；

        以I为圆心、线段IO为半径作圆I；

        设圆H和圆I交于P（P和J位于直线HI同侧）；

        连结直线PI、PH、PJ；

        作三角形PIH的内切圆，并取内切圆上的自由点Q；

        设直线IQ交直线PH于S，直线HQ与直线PI交于R；

        分别过S、R作直线PJ的平行线，与直线JH、JI交于T、U；

        设直线TI、HU交于V；

        选中Q、V，构造V的轨迹，就是所求的椭圆。

        把这个作图过程作成自定义工具——依次选中J、I、H、椭圆，添加新工具。

4、        留一个问题：给出三角形ABC和内部两个点D、E，求作椭圆，使之过D、E两点，且与三角形ABC三边都相切！

5、        给定凸四边形AKLM，P为线段AK上一点，求作椭圆，使之与凸四边形AKLM四条边都相切，而且与AK的切点恰好是P。

        具体的作图步骤是：

        设AL与MK交于U，AK与LM交于O；

        直线PU与LM交于R；

        直线RK与PL交于T；

        直线OT与KL交于Q；

        用第三步里面的自定义工具，作三角形OKL的内切椭圆，使之与三边切于P、Q 、R ；

        这个椭圆就是所求的四边形内切椭圆。

6、        类似问题：

        给定四边形ABCD及内部点E，求作椭圆，使之过点E，且与四边形ABCD的四条边都相切！

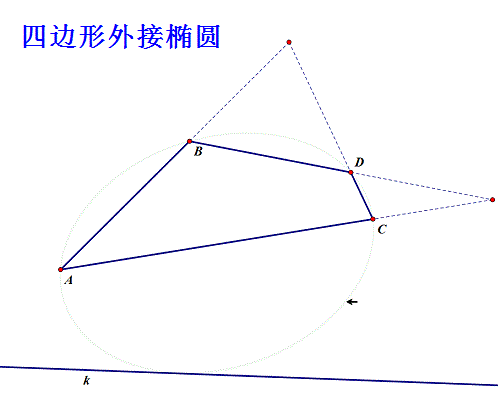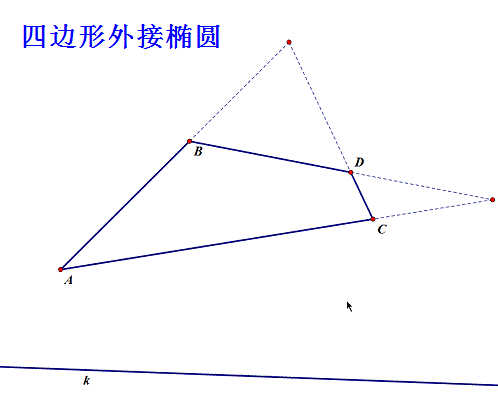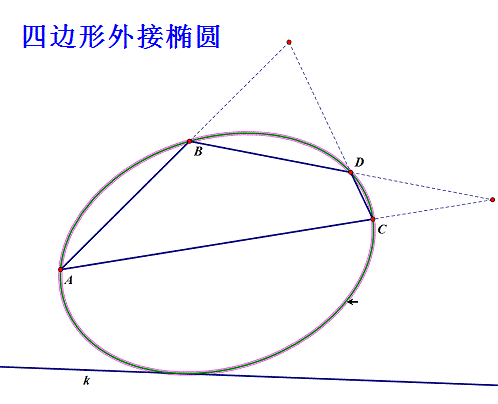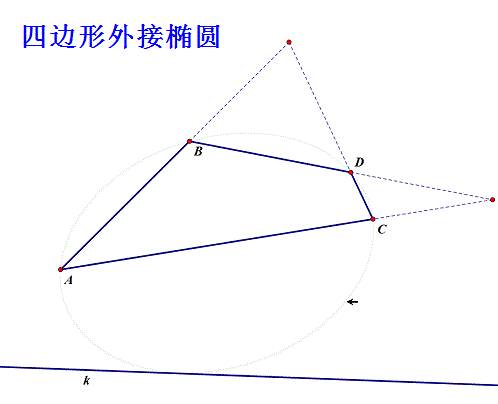
        给定四边形ABCD和直线k，求作椭圆，使之过A、B、C、D四点，且与直线k相切！