【抽象代数】写出正四面体群的一种酉表示

1、在《【抽象代数】正四面体群的三维矩阵表示》，我给出了正四面体群的一个3维的矩阵表示。

本文的后续讨论，就以此为基础。

a={{0,0,1},{1,0,0},{0,1,0}};

b={{0,0,1},{-1,-1,-1},{1,0,0}};

2、给出任意的3*3的可逆矩阵P，那么，PGP'也是群G的一个矩阵表示。

那么，后面的目标，就是寻找这样一个矩阵P，使得PGP'里面的矩阵都是酉矩阵。

先来构造一个G不变型：

B=Total[#\[Transpose]\[Conjugate].#&/@G]/12;

f[x_,y_]:=x.B.y

3、先来寻找一个向量p1和p2，使得：

f[p,p]==1&&f[p0,p0]==1&&f[p,p0]==0

4、再寻找一个与p1、p2都关于给定的G不变型正交的向量p3，且f[p3,p3]==1。

5、这样，我们得到了这个型的一个标准正交基。

6、验证一下，这个确实是型的标准正交基。

7、P'GP就是一个酉表示。

G0=Simplify[Inverse[P].#.P]&/@G

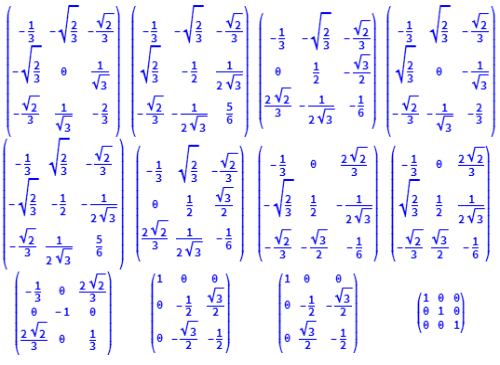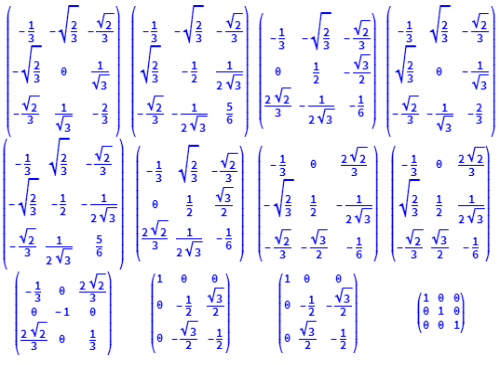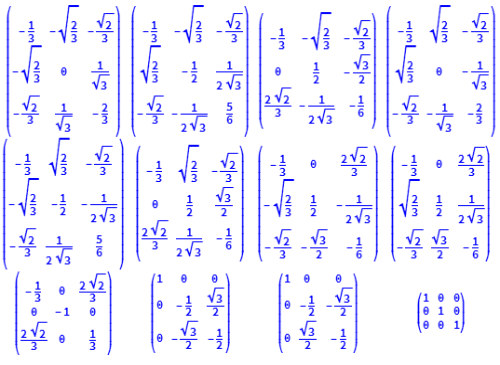
8、验证，里面的矩阵都是酉矩阵。