MATLAB学习与使用：求函数的反函数（finverse）

1、第一，求解下图两个函数f(x)和g(x)的反函数。

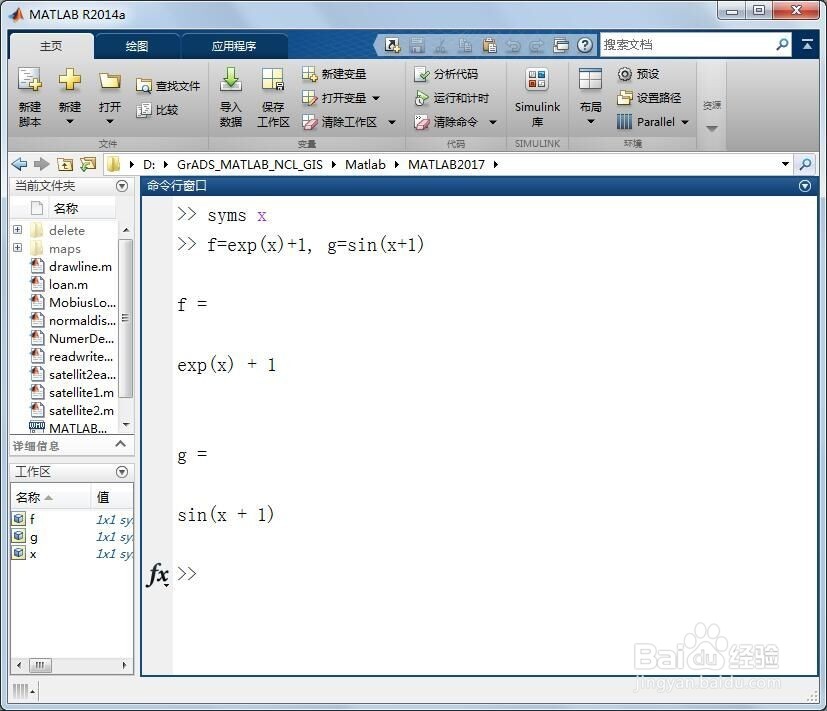
2、第二，先利用syms定义符号变量和上图中的两个函数f(x)和g(x)。在命令行窗口输入如下代码：

syms x

f=exp(x)+1, g=sin(x+1)

回车返回如下结果：

f =

exp(x) + 1

g =

sin(x + 1)

这样就定义好了函数f(x)和g(x)，关于如何定义函数，可以参考百度经验《MATLAB学习与使用：定义函数（3种方法）》。

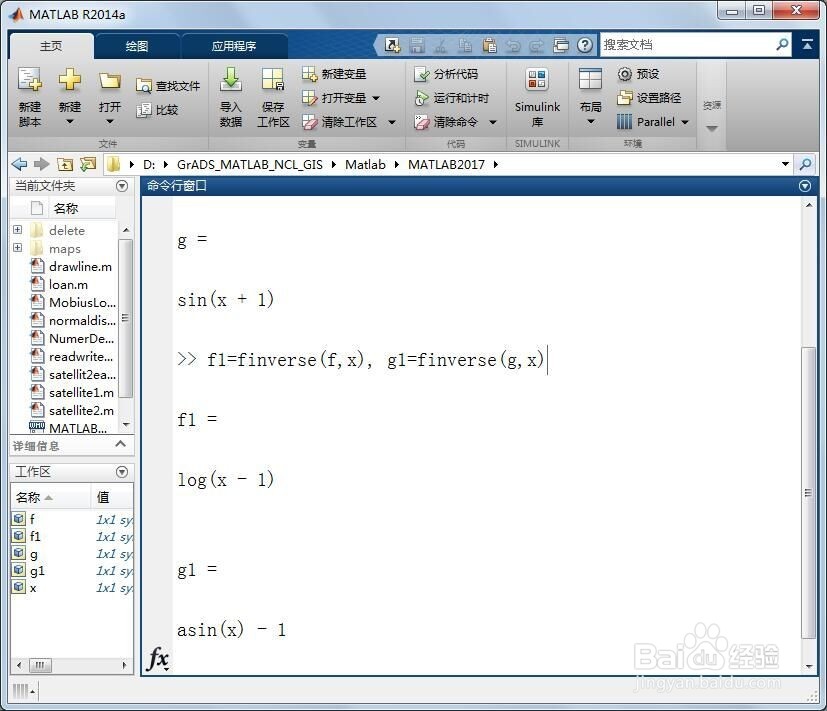
3、第三，利用finverse求解函数f(x)和g(x)的反函数。在命令行窗口紧接着输入如下代码：

f1=finverse(f,x), g1=finverse(g,x)

回车返回如下结果：

f1 =

log(x - 1)

g1 =

asin(x) - 1

这样就得到了f(x)和g(x)的反函数，f1=log(x - 1)，g2=asin(x) - 1。

在MATLAB中，用log(x)表示ln(x)，用asin(x)表示arcsin(x)。

4、第四，还可以利用内联函数（inline）定义f(x)和g(x)，然后再求解它们的反函数。使用clear all; clc清空工作区和命令行窗口，在命令行窗口输入如下代码：

syms x

f=inline('exp(x)+1'), g=inline('sin(x+1)')

回车返回如下结果：

f =

     内联函数:

     f(x) = exp(x)+1

g =

     内联函数:

     g(x) = sin(x+1)

5、第五，在命令行窗口紧接着输入如下代码：

f1=finverse(f(x),x), g1=finverse(g(x),x)

回车返回如下结果：

f1 =

log(x - 1)

g1 =

asin(x) - 1

求得的反函数与第三步一样。需要注意：finverse( )中写得是f(x), g(x)，而不是f,g，这与第三步不同。