状态空间表达式变换为约旦标准型

约旦标准型由于其标准简洁的形式，有利于我们对各种现代控制理论问题的研究，其对状态转移矩阵的求解以及能控能观性的判别等，都具有重要意义。

而要将某个矩阵化为约旦标准型，主要问题，便是——根据系统矩阵A，求变换矩阵T

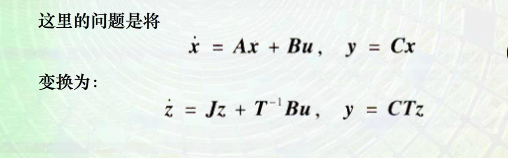
工具/原料

手、脑、心

方法/步骤

A阵为任意形式

（1）A阵的特征值无重根时，如图

A阵为任意形式

（2）A阵的特征值有重根时

设A的特征根有q个λ1的重根，其余（n-q）个根为互异根，先不加证明地引出变换矩阵T的计算公式，如下：

         T=(P1，P2，···，Pq,Pq+₁,···,Pn)

其中，Pq+₁,···,Pn是对应于（n-p）个单根的特征矢量，求法同前，对应于q个λ1重根的矢量P1，P2，···，Pq的求得，应根据下式计算（如图）：

看图，显然，P1仍为λ1对应的特征矢量，其余P2，···,Pq则称之为广义特征矢量。

A阵为标准型

（1）A阵的特征值无重根时，如图

A阵为标准型

（2）A阵的特征值有重根时，如图

A阵为标准型

（3）A阵的特征值有共轭复根时，如图