Fourier变换的应用——图像去噪

1、把图片转化为图片数据：

data = ImageData[img];

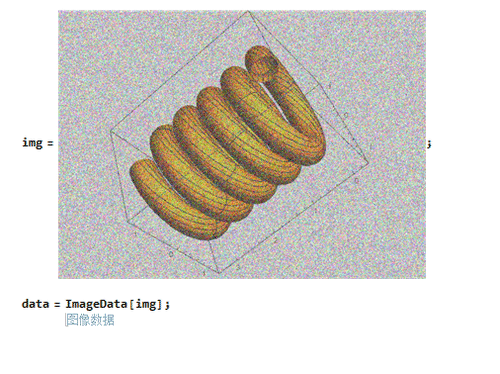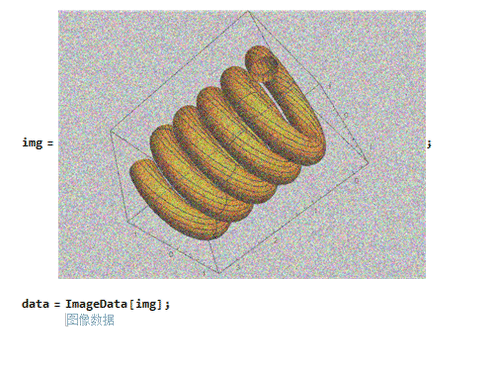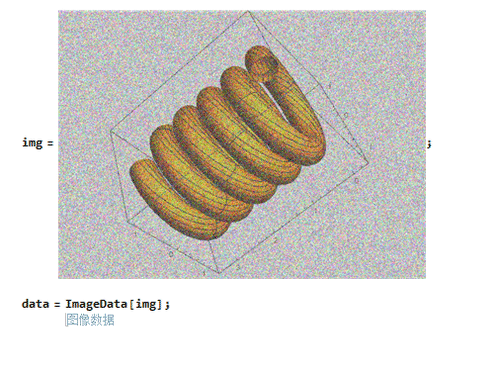
2、对图片数据进行Fourier变换：

d0 = Fourier[data[[All, All, #]]] & /@ {1, 2, 3}

注意，图片是三通道图片，要分别对每一个通道单独变换。

对变换后的数据，直接合成图片，结果如下。

3、如果对变换后的数据，取绝对值（复数取模长），再合成图片，效果如下。

Image[#] & /@ Abs@d0 // ColorCombine

4、看一下给出的图片的尺寸：

{w, h} = ImageDimensions[img]

w代表宽度，h代表高度。

5、制造一个过滤器，把步骤三里面那些暗色的区域对应的数据变为0；其实，这些区域代表着噪音对应的数据。

p = 0.4;

filter = Table[

   If[Abs[(r - (h/2))/h] > p && Abs[(c - (w/2))/w] > p, 1, 0], {r, 1, 

    h}, {c, 1, w}];

过滤器又叫掩膜。下图是p=0.4的时候的掩膜。

6、把这个过滤器和Fourier变换同时起作用，可以在一定程度上过滤掉噪音：

Image /@ (Abs /@ (Fourier[ImageData[img][[All, All, #]]]*

        filter) & /@ {1, 2, 3}) // ColorCombine

如下图，只有角落里面那些亮色数据得以保存。

7、经过Fourier变换、去噪，在对数据进行逆Fourier变换，就可以合成去噪后的图片。

ColorCombine[

 Image[Abs@

     InverseFourier[

      Fourier[ImageData[img][[All, All, #]]]*filter]] & /@ {1, 2, 3}]

下图使用的是p=0.4的过滤器去噪，得到的图片。噪音没了，但是图像很模糊。

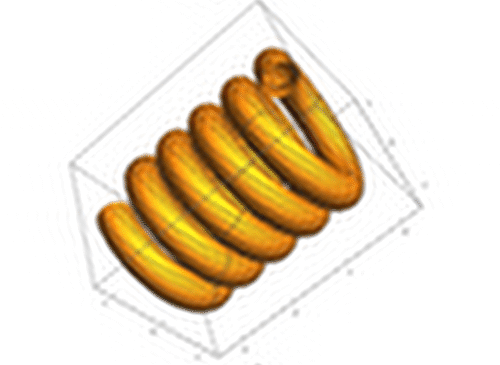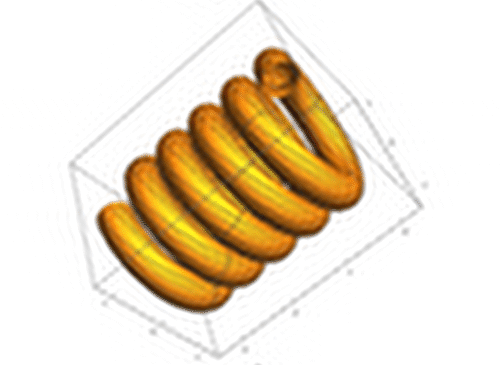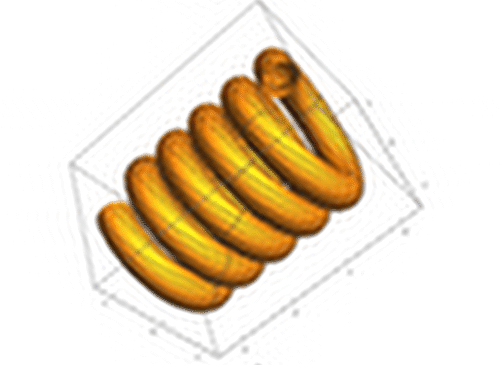
8、当p=0.2的时候，掩膜图片如下。

保留下来的像素明显增多了。

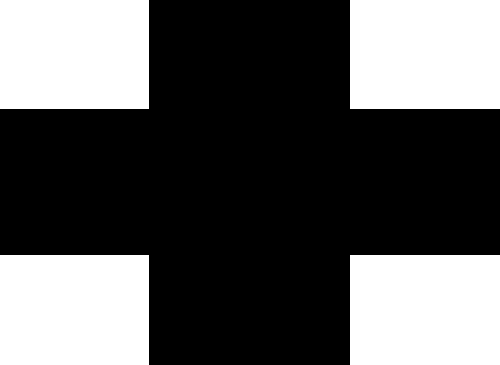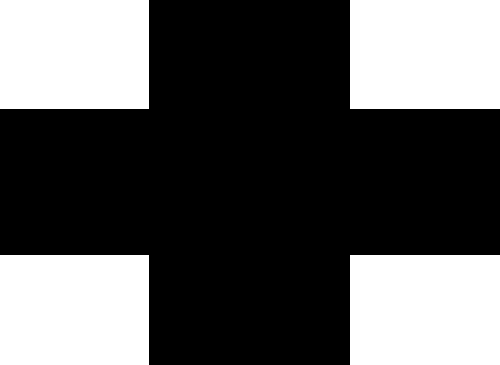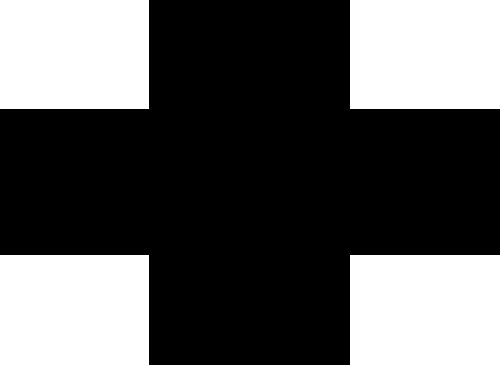
9、看看用p=0.2的过滤器，得到的图片，变的很清晰了。

10、当p=0.01的时候，掩膜和最终效果如下。