Mathematica基础——用Integrate 求不定积分

1、        求1/(x^2+x + 1)的不定积分，并返回“传统形式”：

Integrate[1/(x^2+x + 1), x]//TraditionalForm

        注意Mathematica的一些“习惯”：

        返回的结果一般不是传统形式，需要用命令函数TraditionalForm进行转化 ；

        返回的结果没有后面的常数项，但是你自己不要忽略常数项；

        返回的结果里面的(tan(x))^-1表示tan(x）的反函数arctan(x)。

2、        还可以在代码前面连续输入两个“=”，Mathematica会自动链接到网络上进行计算，并返回相应的步骤：

==Integrate[1/(x^2+x + 1), x]//TraditionalForm

        运行之后，点击“Step by step Solution”，就能看到具体的计算积分的步骤。

3、        我们可以调用“数学面板”进行输入，写好的代码直接复制过来，是这样子滴：

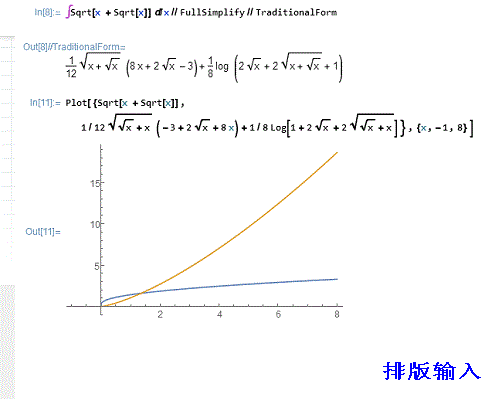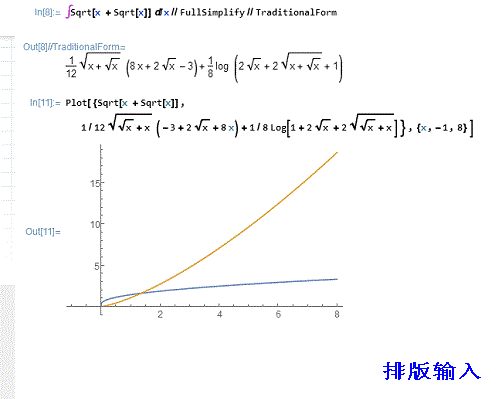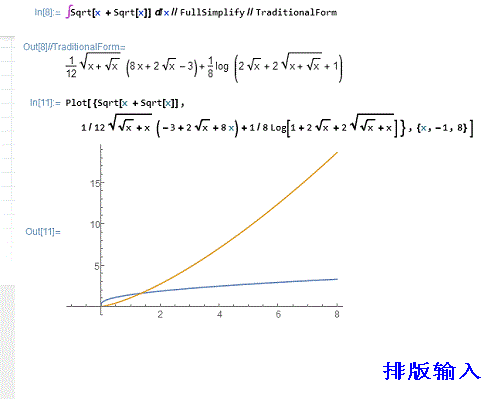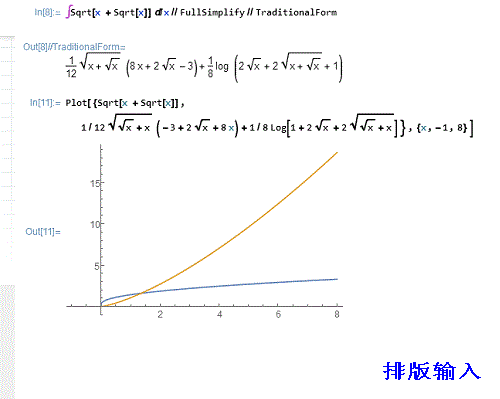
\[Integral]Sqrt[x + Sqrt[x]] \[DifferentialD]x//FullSimplify//TraditionalForm

        这里对结果先化简（FullSimplify），后化形（TraditionalForm），然后再作积分函数与原来的函数的图像，加以比较：

Plot[{Sqrt[x + Sqrt[x]],%},{x,-1,8}]

4、        有一些函数是无法求出不定积分的，如sin (sin (x))：

Integrate[Sin[Sin[x]],x]//TraditionalForm

        此时会直接返回源代码！

5、        有时候，一些简单函数，也是无法求积分的，如下面的分段函数 ：

Integrate[Abs[x + Abs[x]^2], x]//TraditionalForm

        但是加上“假设（Assumptions）”条件的话 ，有时候是可以求积分的（本例中，只是把x限定为实数而已）：

Integrate[Abs[x + Abs[x]^2], x, Assumptions -> x\[Element]Reals]//TraditionalForm

Plot[{Abs[x + Abs[x]^2],%},{x,-2.6,1.6}]