高中数学必修2:平面解析几何——椭圆经典习题

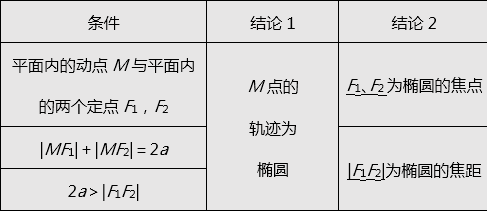
1、��椭圆的定义

2、椭圆的标准方程和几何性质

1、辨明两个易误点

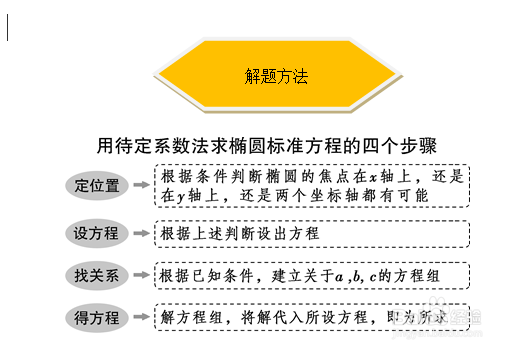
2、��求椭圆标准方程的两种方法

1、椭圆的定义及应用

(1)设F1，F2分别是椭圆E：x2＋＝1(0＜b＜1)的左、右焦点，过F1的直线l与E相交于A，B两点，且|AF2|，|AB|，|BF2|成等差数列，则|AB|＝(　　)

(2)(2017·徐州模拟)已知F1、F2是椭圆C：＋＝1(a＞b＞0)的两个焦点，P为椭圆C上的一点，且PF1⊥PF2，若△PF1F2的面积为9，则b＝________．

2、椭圆的标准方程

(2017·湖南省东部六校联考)已知椭圆的中心在原点，离心率e＝，且它的一个焦点与抛物线y2＝－4x的焦点重合，则此椭圆方程为(　　)

(2)设F1，F2分别是椭圆E：x2＋＝1(0<b<1)的左、右焦点，过点F1的直线交椭圆E于A，B两点，若|AF1|＝3|F1B|，AF2⊥x轴，则椭圆E的标准方程为________．

3、椭圆的几何性质

 (2016·高考全国卷丙)已知O为坐标原点，F是椭圆C：＋＝1(a＞b＞0)的左焦点，A，B分别为C的左，右顶点．P为C上一点，且PF⊥x轴．过点A的直线l与线段PF交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为(　　)

(2017·合肥质检)如图，焦点在x轴上的椭圆＋＝1的离心率e＝，F，A分别是椭圆的一个焦点和顶点，P是椭圆上任意一点，则·的最大值为________．

4、直线与椭圆的位置关系

 (2016·高考全国卷甲改编)已知A是椭圆E：＋＝1的左顶点，斜率为k(k＞0)的直线交E于A，M两点，点N在E上，MA⊥NA.

(1)当|AM|＝|AN|时，求△AMN的面积；

(2)当2|AM|＝|AN|时，证明：4k3－6k2＋3k－8＝0.

5、(2017·江西五市八校二模)已知正数m是2和8的等比中项，则圆锥曲线x2＋＝1的焦点坐标为(　　)

6、(2017·湖北八校联考)设F1，F2分别为椭圆＋＝1的两个焦点，点P在椭圆上，若线段PF1的中点在y轴上，则的值为(　　)

7、(2017·福建省毕业班质量检测)若椭圆上存在三点，使得这三点与椭圆中心恰好是一个正方形的四个顶点，则该椭圆的离心率为(　　)