Mathematica应用——继续考察球面曲线
1、 曲面,一般是由含两个参数的参数方程所确定,事实上,就是把一个平面上的矩形区域投影到球面上。
例如,我们来绘制一个单位球面,就是一个矩形区域的投影。这个过程,可以称为球面变换。
RegionPlot[0 <= u <= 2 Pi && 0 <= v <= Pi, {u, -1, 7}, {v, -1, 5},
AspectRatio -> Automatic]
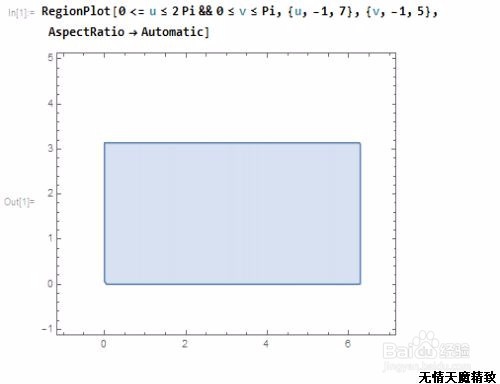
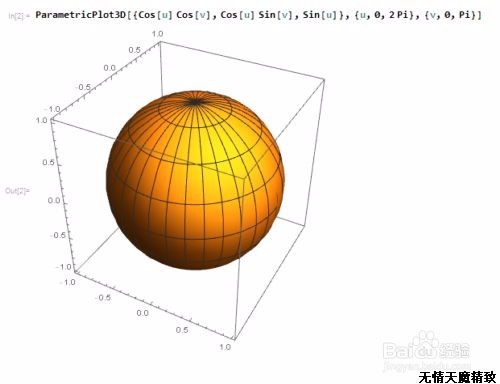
2、 单位球面对应的参数方程是{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]},通过限定u和v的值,使之分别由小变大,可以体现这个具体的作图过程。
Manipulate[
ParametricPlot3D[{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}, {u, 0, a0},
{v, 0, Pi}, PlotRange ->1.1], {a0, 0.1, 2 Pi, 0.1}]
类似的其余情形,大家可以自己实验!

3、 给定一个曲面,要绘制曲面上的曲线,可以有两种方法: 一种方法是,用两个曲面相交产生曲线;另一个方法是曲面上直接绘制曲线。
用两个曲面相交产生曲线,这个方法是复杂的。因为要绘制这条相交线,必须确定特定的曲面,但是一条曲线所张的曲面可以说是无限多。
所以说,用曲面相交的方法绘制曲面上的曲线,不如直接在曲面上绘制曲线来的容易。
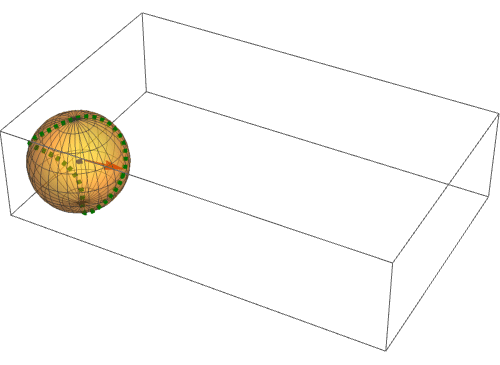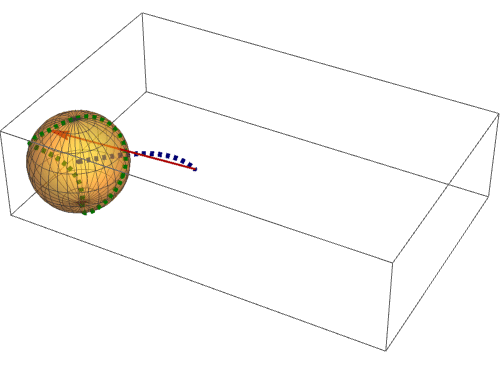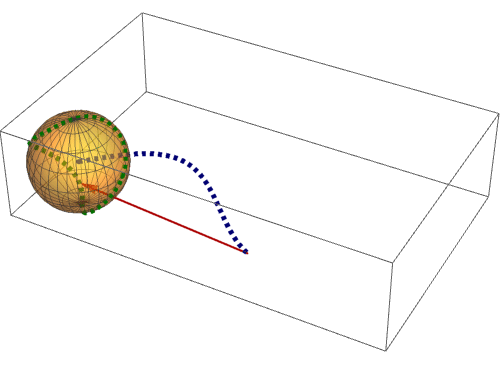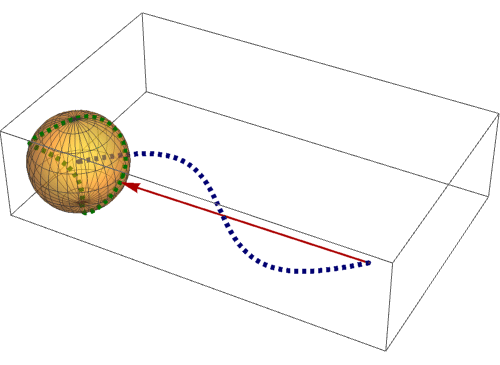
仍旧以球面曲线为例:继续延续第一步的结果,我们先在平面上的矩形区域内绘制一条参数曲线:
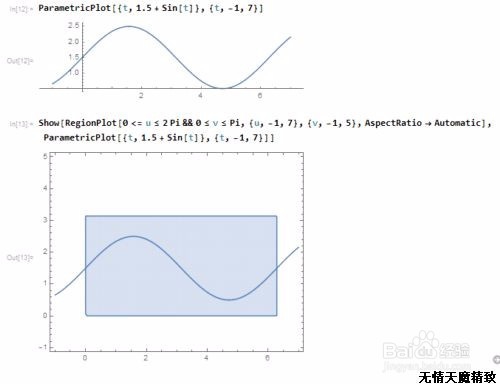
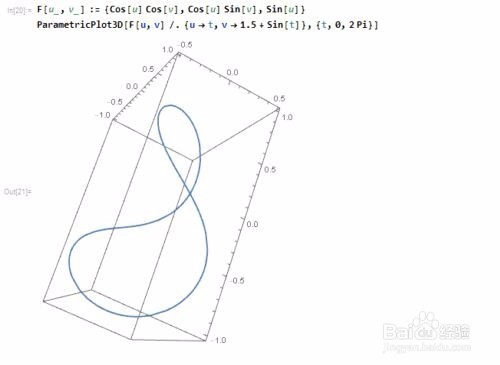
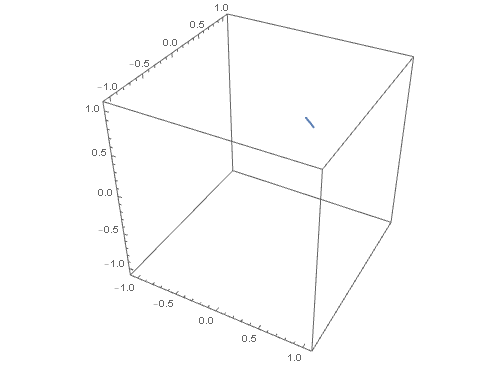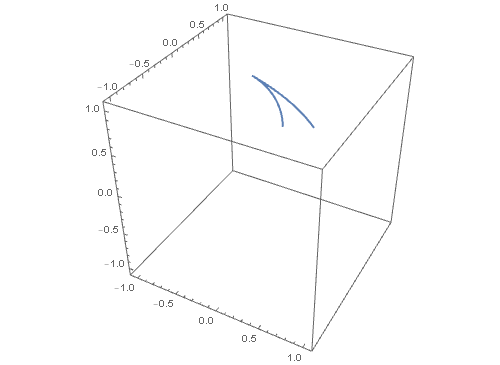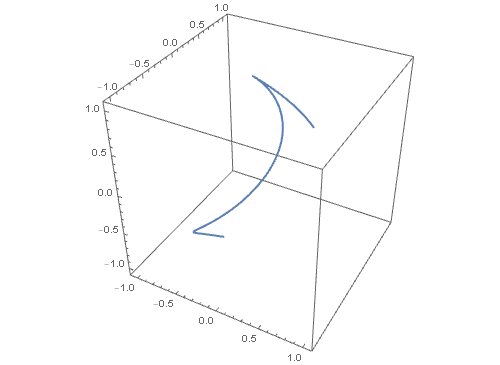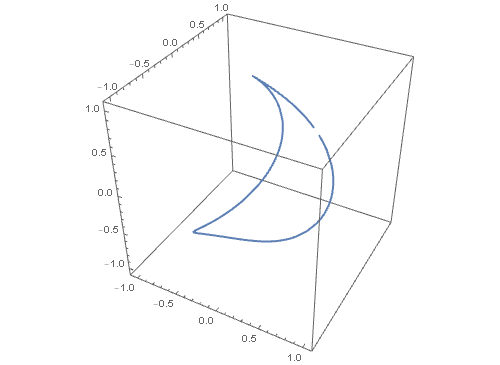
4、 把上面这个曲线投影到球面上,看看这条曲线会变成什么样子 :
F[u_, v_] := {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}
ParametricPlot3D[F[u, v] /. {u -> t, v -> 1.5 + Sin[t]}, {t, 0, 2 Pi}]
注意看,这个过程是,矩形区域球面化的同时,里面的曲线也球面化了,这其实仍旧是球面变换,只不过多了个变换对象!
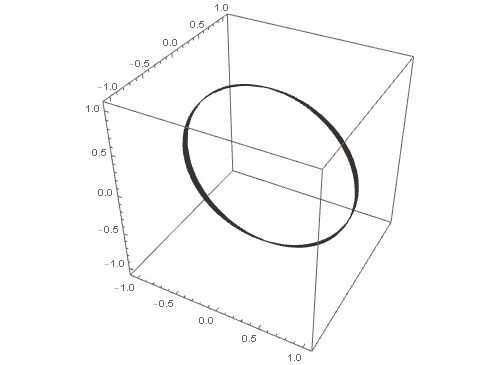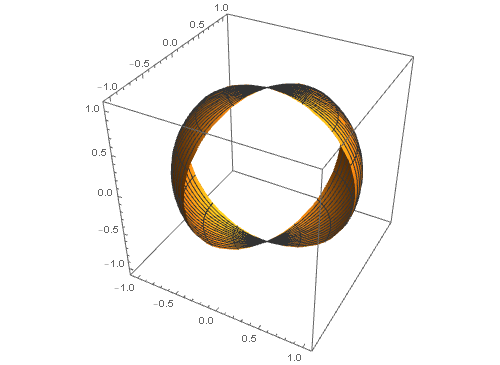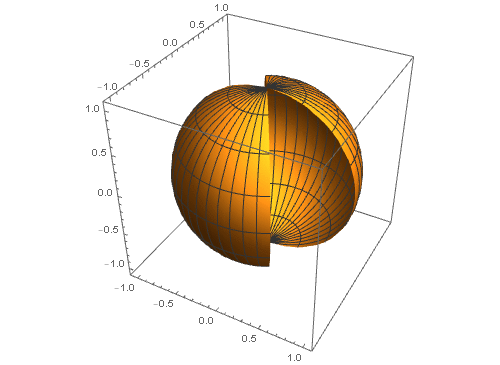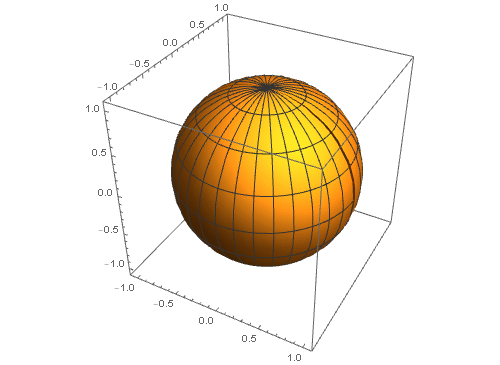
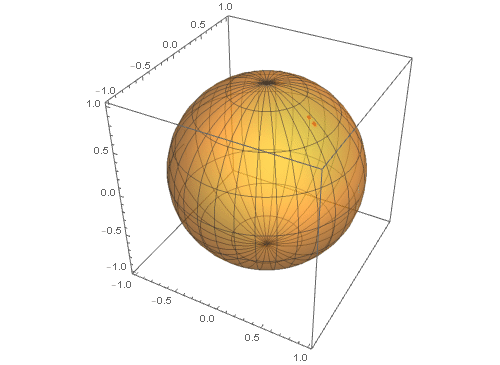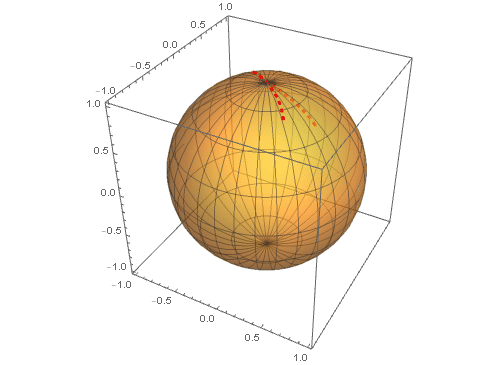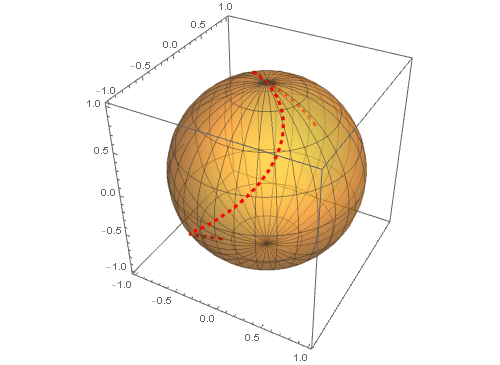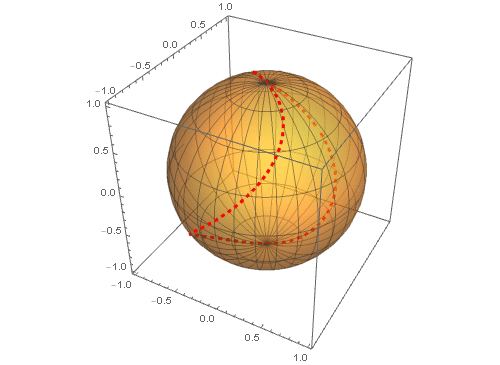
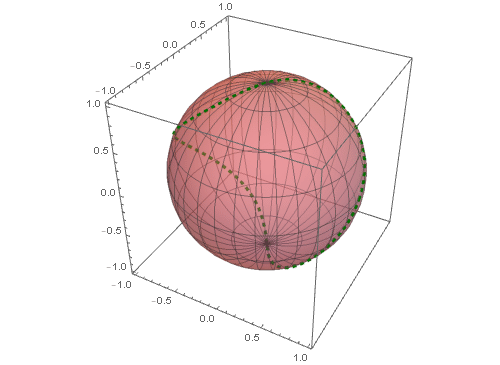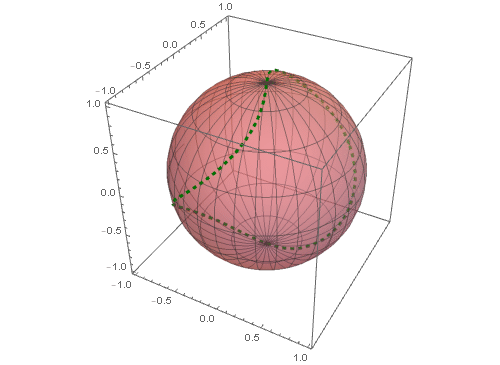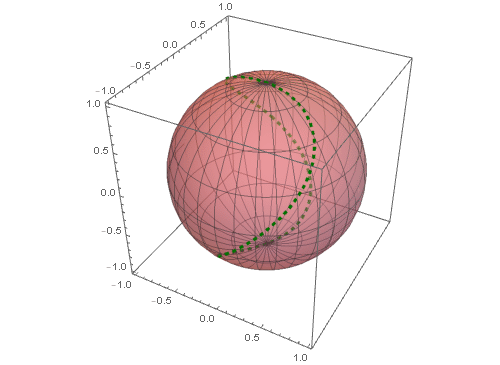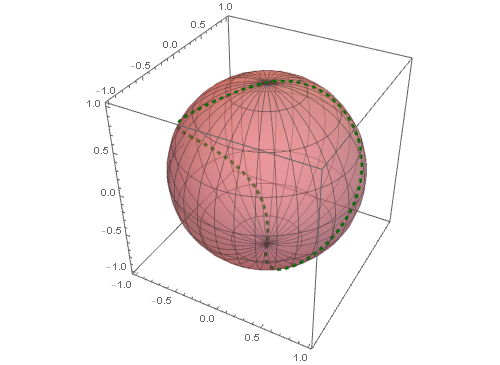
5、 把这条球面曲线和球面一块画出来:
F[u_, v_] := {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}
Show[ParametricPlot3D[F[u, v], {u, 0, 2 Pi}, {v, 0, Pi},
PlotStyle -> Opacity[0.5]],
ParametricPlot3D[
F[u, v] /. {u -> t, v -> 1.5 + Sin[t]}, {t, 0, 2 Pi},
PlotStyle -> {Red, Thickness[0.01], Dashed}]]
其中对球面进行了半透明化操作,可以更好地观察这条球面曲线(图中的红色虚线)。
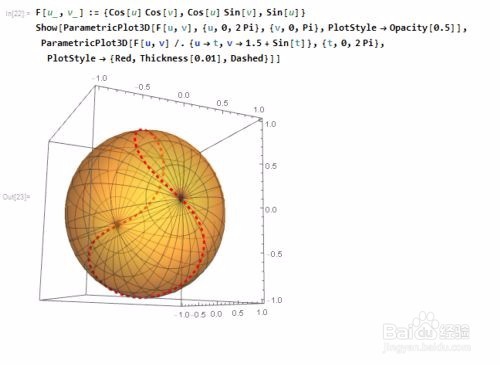
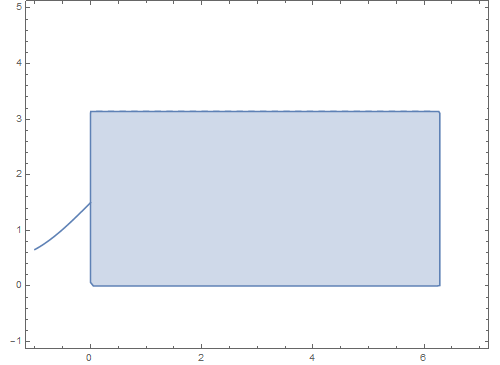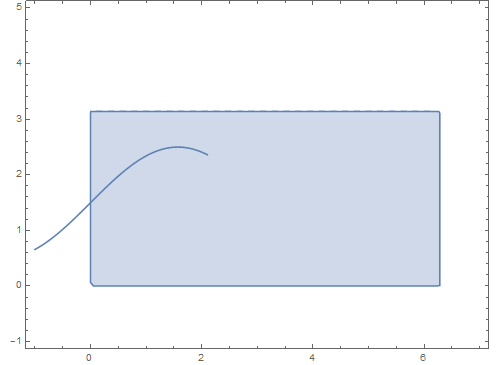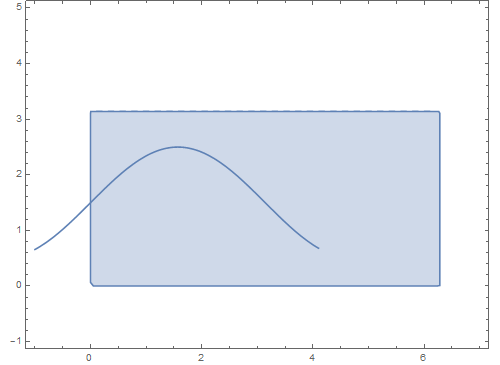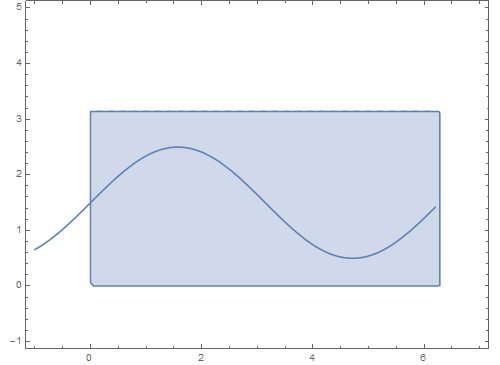
6、 使参数t的最大值由小变大,可以实现这个球面曲线的作图过程:
Manipulate[
Show[RegionPlot[
0 <= u <= 2 Pi && 0 <= v <= Pi, {u, -1, 7}, {v, -1, 5},
AspectRatio -> Automatic],
ParametricPlot[{t, 1.5 + Sin[t]}, {t, -1, a0}]], {a0, 0, 2 Pi}]
和
Manipulate[
ParametricPlot3D[{Cos[t] Cos[1.5 + Sin[t]], Cos[t] Sin[1.5 + Sin[t]],
Sin[t]}, {t, 0, a0}], {a0, 0.0001, 2 Pi}]
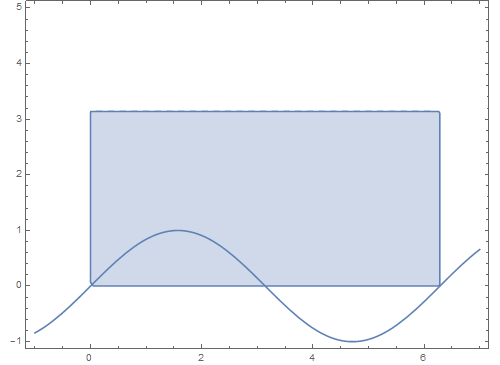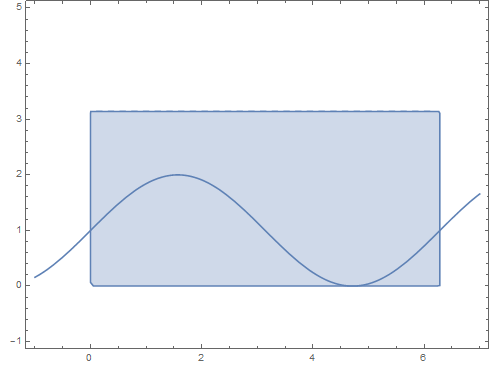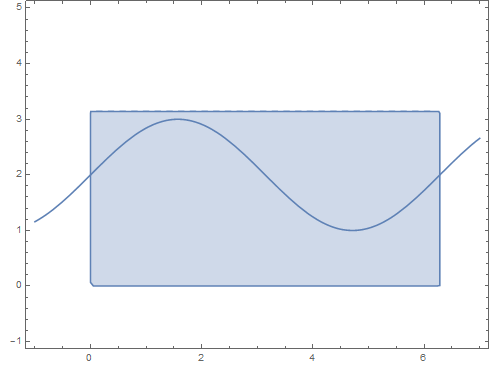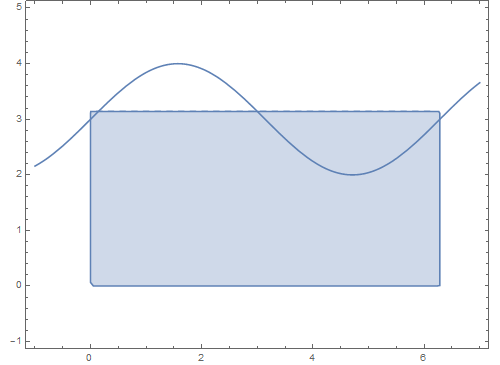
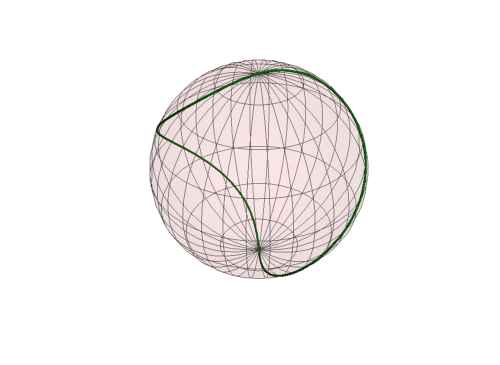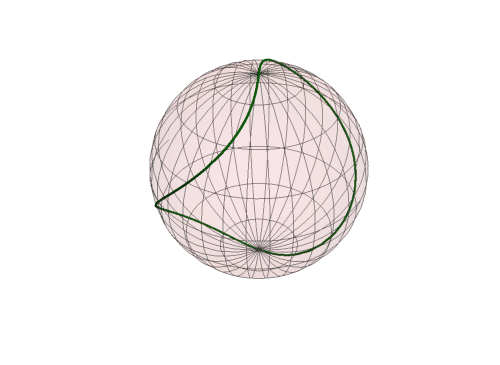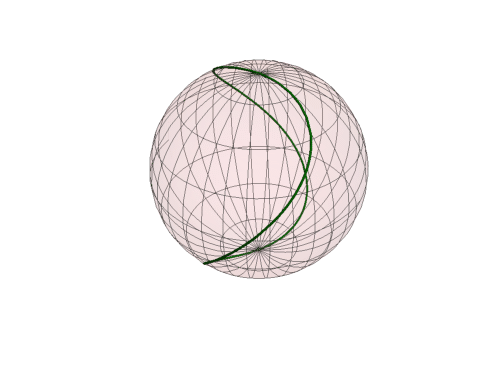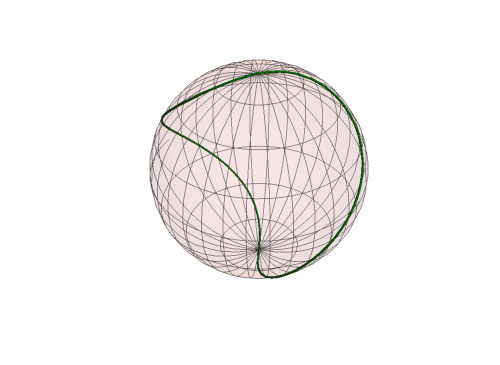
7、 如果在矩形区域内上下平移这条曲线,看看它在球面上的对应图形会发生什么变化:
Manipulate[
Show[RegionPlot[
0 <= u <= 2 Pi && 0 <= v <= Pi, {u, -1, 7}, {v, -1, 5},
AspectRatio -> Automatic],
ParametricPlot[{t, b0 + Sin[t]}, {t, -1, 7}]], {b0, 0, 3}]
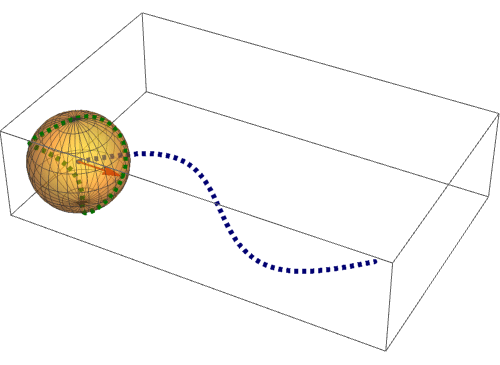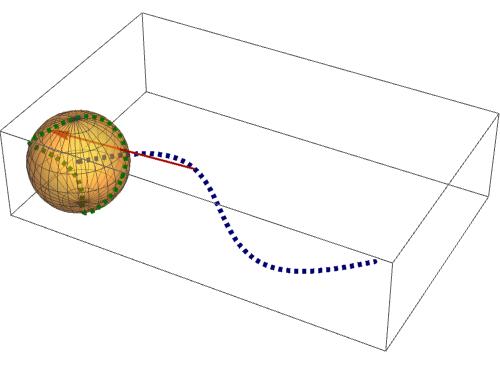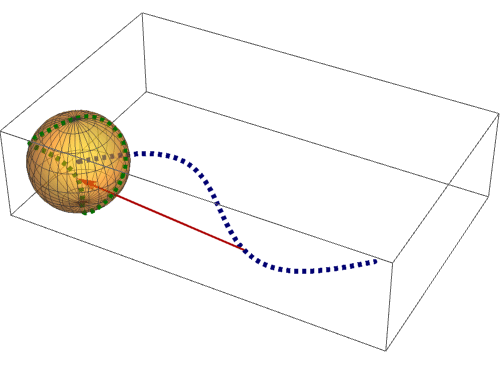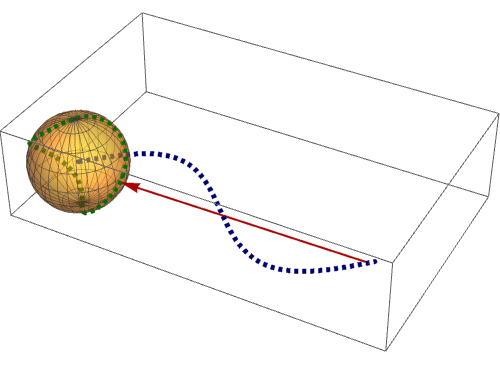
8、 下面来看看,平面上的曲线是怎么投影到球面上去的。一个点一个点的对应:
Manipulate[
Show[
ParametricPlot3D[{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]},
{u, 0, 2 Pi}, {v, 0, Pi}, PlotStyle -> Opacity[0.5]],
ParametricPlot3D[{tt, Sin[tt], 0}, {tt, 0, b0}],
ParametricPlot3D[{Cos[t] Cos[Sin[t]], Cos[t] Sin[Sin[t]], Sin[t]},
{t, 0, b0}, PlotStyle -> {Red, Thickness[0.01], Dashed}]],
{b0, 0.001, 2 Pi}]
可以发现,球面曲线的首尾相接,尽管对应的平面曲线不是这样!