matlab中的矩阵指数
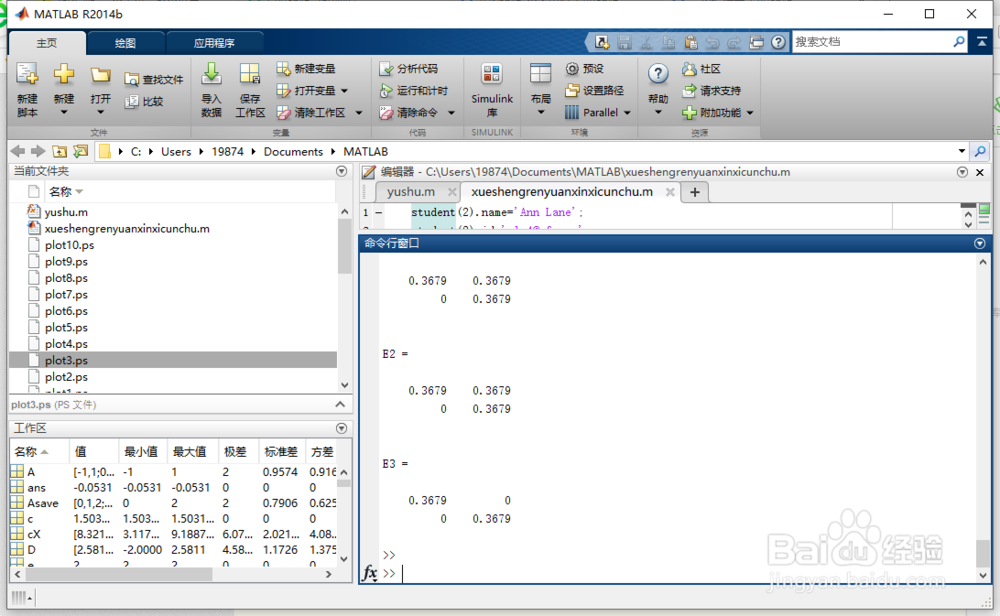
1、从矩阵A开始
A = [0 1 2; 0.5 0 1; 2 1 0]
Asave = A;
2、按“Enter”键。
得图1所示。
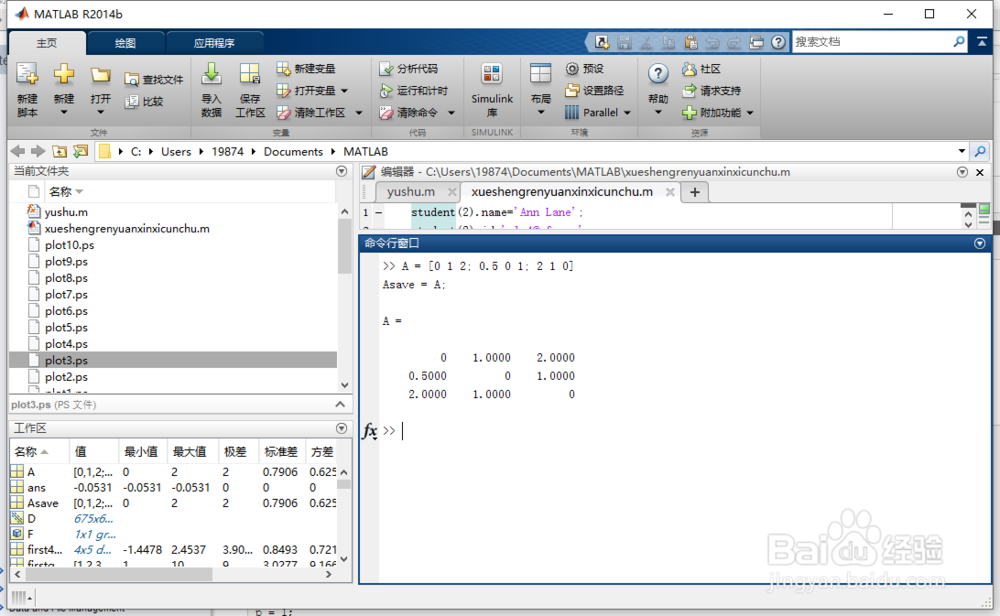
3、缩放和平方
是算法11.3.1在Golub和Van Loan中的实现,矩阵计算,第3版。
% Scale A by power of 2 so that its norm is < 1/2 .
[f,e] = log2(norm(A,'inf'));
s = max(0,e+1);
A = A/2^s;
% Pade approximation for exp(A)
X = A;
c = 1/2;
E = eye(size(A)) + c*A;
D = eye(size(A)) - c*A;
q = 6;
p = 1;
for k = 2:q
c = c * (q-k+1) / (k*(2*q-k+1));
X = A*X;
cX = c*X;
E = E + cX;
if p
D = D + cX;
else
D = D - cX;
end
p = ~p;
end
E = D\E;
% Undo scaling by repeated squaring
for k = 1:s
E = E*E;
end
E1 = E
4、按“Enter”键。
得图2所示。
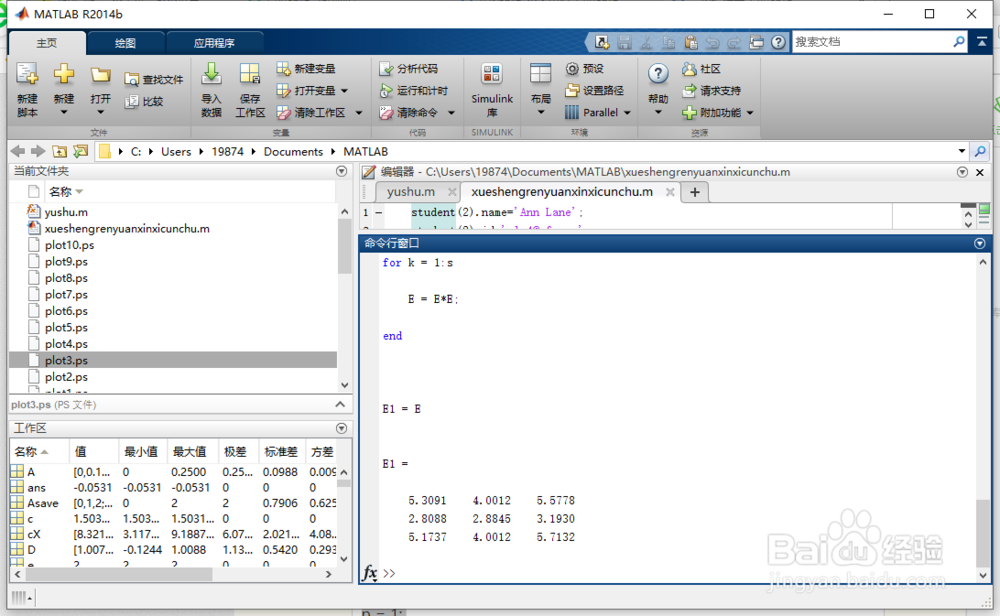
5、exmdem2使用了矩阵指数的经典定义。
A = Asave;
% Taylor series for exp(A)
E = zeros(size(A));
F = eye(size(A));
k = 1;
while norm(E+F-E,1) > 0
E = E + F;
F = A*F/k;
k = k+1;
end
E2 = E
6、按“Enter”键。
得图3所示。
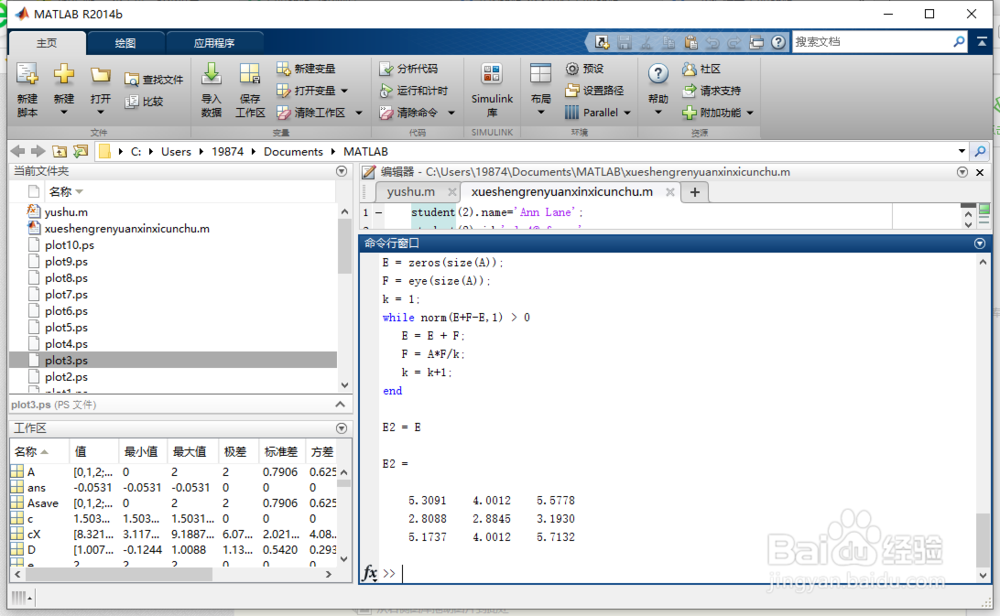
7、通过特征值和特征向量的矩阵指数
expmdemo3假设矩阵具有完整的特征向量集。作为一种实用的数值方法,精度取决于特征向量矩阵的条件。
A = Asave;
[V,D] = eig(A);
E = V * diag(exp(diag(D))) / V;
E3 = E
8、按“Enter”键。
得图4所示。

9、比较结果
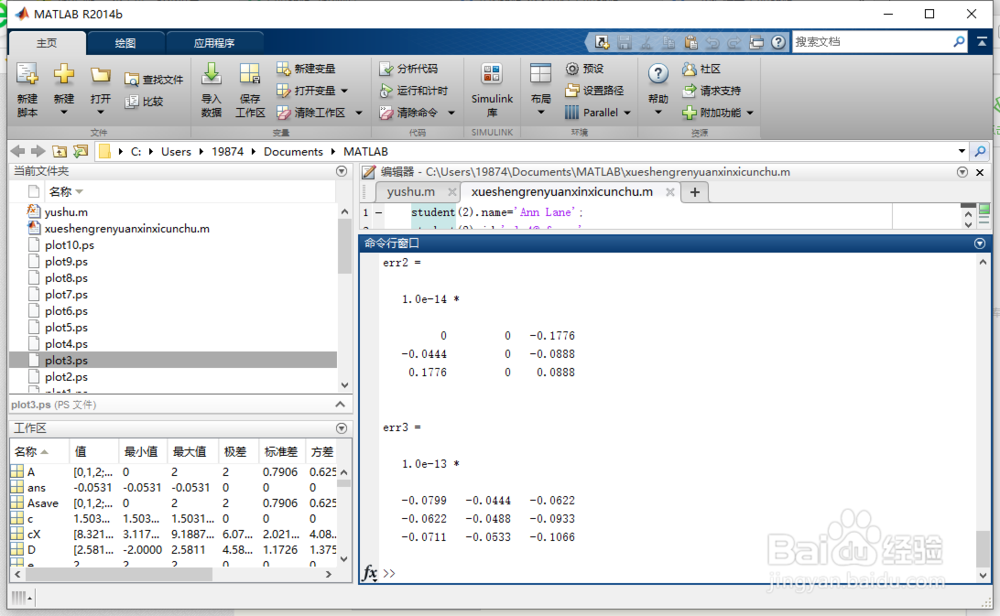
对于这个矩阵,它们都做得同样好。
E = expm(Asave);
err1 = E - E1
err2 = E - E2
err3 = E - E3
10、按“Enter”键。
得图5所示。
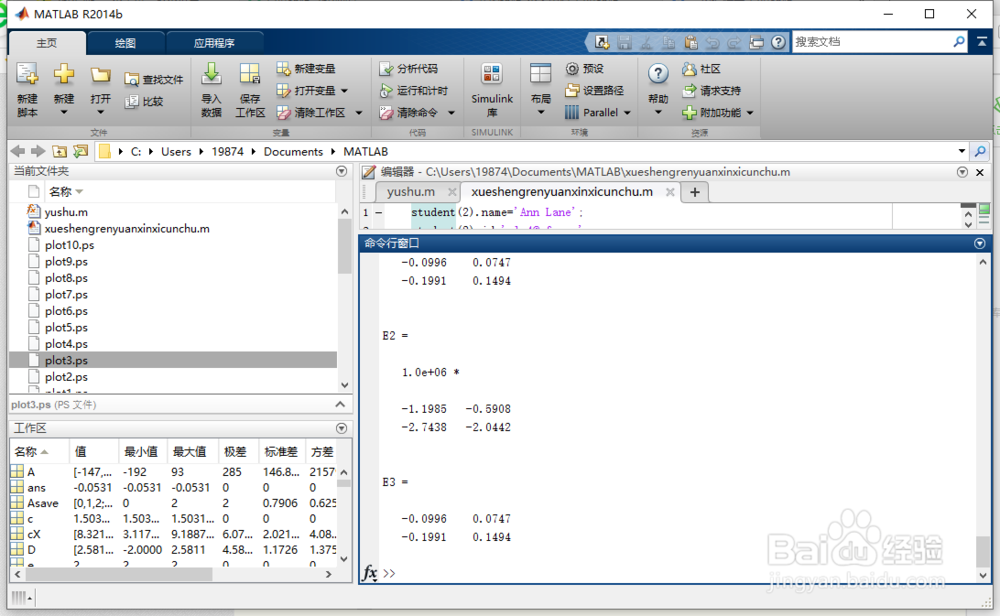
11、泰勒级数失败
下面是一个矩阵,泰勒级数中的项在变为零之前变得非常大。因此,expmdemo2失败。
A = [-147 72; -192 93];
E1 = expmdemo1(A)
E2 = expmdemo2(A)
E3 = expmdemo3(A)
12、按“Enter”键。
得图6所示。
13、这是一个没有完整特征向量集合的矩阵,因此,expmdemo3失败了。
A = [-1 1; 0 -1];
E1 = expmdemo1(A)
E2 = expmdemo2(A)
E3 = expmdemo3(A)
14、按“Enter”键。
得图7所示。