初中数学如何巧妙运用换元法？

1、一些较复杂的题目中，巧妙的运用换元法，可以有效提高解题效率。

引入例题: 化简[23-4*(33)^(1/2)]^(1/2)

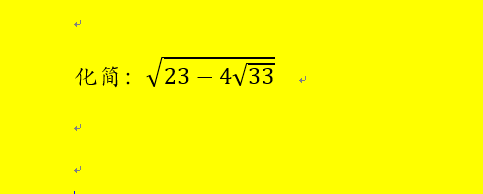
2、观察后发现，根号下的23-4*(33)^(1/2)可以联想到平方差公式。

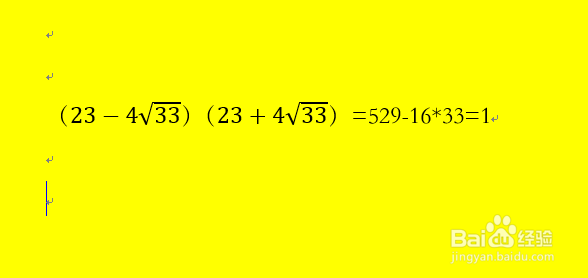
3、设x=[23-4*(33)^(1/2)]^(1/2)  ,  y=[23+4*(33)^(1/2)]^(1/2)

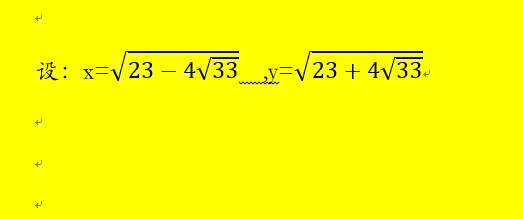
4、可得：xy=1,且x^2+y^2=46

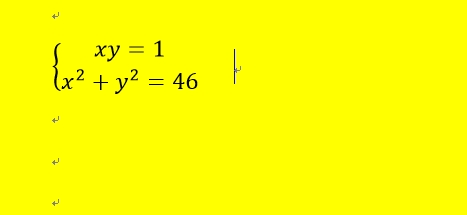
5、由上述可得：

（x+y）^2=x^2+y^2+2xy=46+2=48

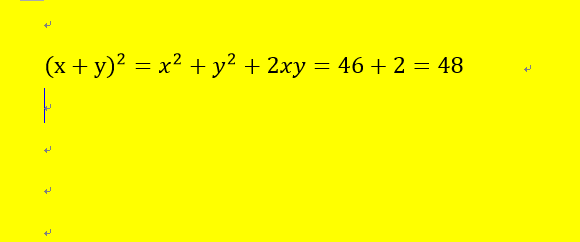
6、因为y>x>0，所以x+y=4*(3)^(1/2)

7、由xy=1，x+y=4*(3)^(1/2)可得：

x,y是一元二次方程m^2-4*(3)^(1/2)*m+1=0的两个实数根。

8、解之得：

m=2*(3)^(1/2)+(11)^(1/2)或2*(3)^(1/2)-(11)^(1/2)

9、所以x=2*(3)^(1/2)-(11)^(1/2)

化简完毕。