Mathematica基础——Factor的简单应用
1、 我们先来尝试着分解x^10-1:
Factor[x^10 - 1]
答案是:
(x-1) (x+1) (x^4-x^3+x^2-x+1) (x^4+x^3+x^2+x+1)

2、 对于分式,通分+分解因式:
Factor[-((2 + x)//(x^2 - 4 y^2)) + (2 x^2 + x^3)//(x^2 - 4 y^2)]

3、 x^4+1在实数域范围内是不能分解的:
Factor[1 + x^4]
但是,我们可以扩充数域,使之可以分解因式:
Factor[1 + x^4,Extension -> Sqrt[2]]

4、 可以分解a^2 + 2 a x + x^2:
Factor[a^2 + 2 a x + x^2]
但是,却不能分解2 + 2 Sqrt[2] x + x^2:
Factor[2 + 2 Sqrt[2] x + x^2]
Extension->Automatic 会把数域自动扩充到涵盖所有系数的域上:
Factor[2 + 2 Sqrt[2] x + x^2,Extension -> Automatic]

5、 在Gauss整数范围内分解因式1+x^2:
Factor[1 + x^2,GaussianIntegers -> True]
再试试:
Factor[1 + x^2,Extension -> I]

6、 三角函数的分解:
Factor[Sin[x] + Sin[y]]
但是加上一个限制条件“Trig -> True”之后
Factor[Sin[x] + Sin[y],Trig -> True]

7、 用来检验一个特殊公式:
Factor[Sin[x]^2 - Sin[y]^2, Trig -> True] // TraditionalForm
真是一步到位!
这个公式在《n倍角公式的证明和应用》一文里得到了重要的应用!

1、 我们在实数范围内来分解x^200 - 1的因式:
Factor[x^200 - 1]
并看看结果有几个因式:
Length[%]

2、 扩充数域之后,再来看看是什么情景:
Factor[1 + x^2,Extension -> I]

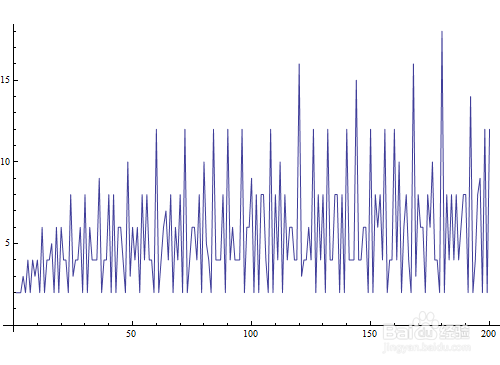
3、 尝试着画出不同代数式在实数范围内分解因式之后,因式个数的图形:
ListLinePlot[Table[Length[Factor[x^n - 1]],{n, 200}]】
这里不考虑扩充数域之后的情景,因为太费时间了!