矩阵乘法在什么时候可以满足交换律？

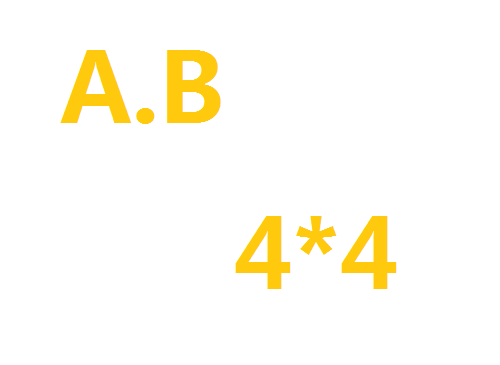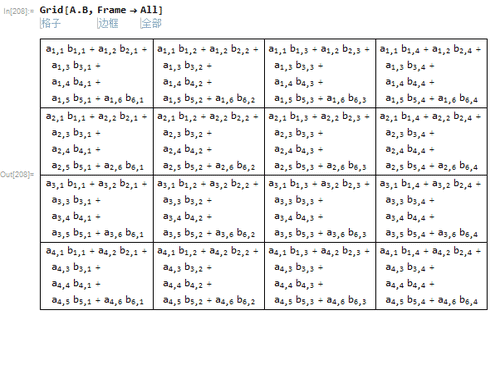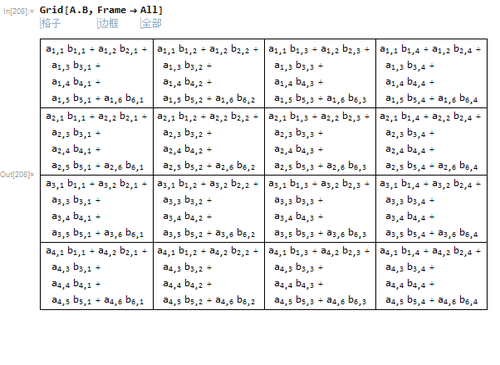
1、给定矩阵A（4*6）和B（6*5）。

2、A.B的结果如下。

3、但是B.A是没有意义的。

具体原因，见下面的动态图。

所以，此时AB和BA就不可能相等。

1、假设A和B分别是4*6和6*4的矩阵。

2、那么A.B就是4*4的矩阵。

3、而BA是6*6的矩阵；

所以，AB和BA也不可能相等。

1、把A和B限定为阶数相同的方阵，才有可能实现AB=BA。

那么假设A和B都是4阶方阵。

2、AB和BA都是4阶方阵，但是AB和BA仍旧未必相等。

3、如果AB=BA，那么AB-BA应该是0矩阵。

由于数据太复杂，临时把4阶方阵换成3阶方阵：

A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};

B = {{8 p, 8 q, 8 r}, {10 q + 4 r, 8 p - 5 q + 14 r, 

   12 q + 8 r}, {4 (q + 4 r), 2 (7 q + 6 r), 8 (p + q + 2 r)}};

此时，AB=BA。

看样子，AB=BA与A、B是不是对称矩阵，没有必然关系。