怎么理解共轭类、中心化子、类方程？

1、三阶置换群S3是由两个元素生成的：

x：对换第一个元素和第二个元素；

y：轮换，第二个元素跑到第一个位置，第三个元素跑到第二个位置，第一个元素跑到第三个位置；

如果原来是{a, b, c}的话，那么执行x操作，就变成了{b, a, c}；

执行y操作，就变成了{b, c, a}。

2、x操作是二阶的，因为x·x=1，表示恒等变换；

y操作是三阶的，因为y·y·y=1。

实际上，S3只有6个元素，而且都是用x和y的组合操作实现的。

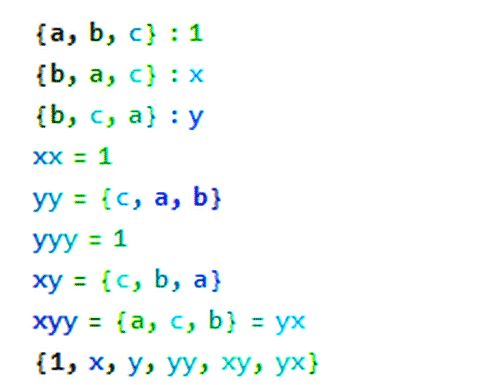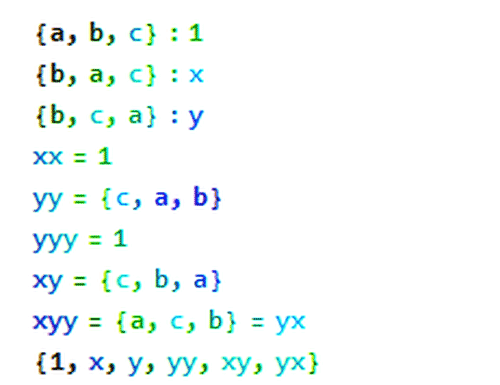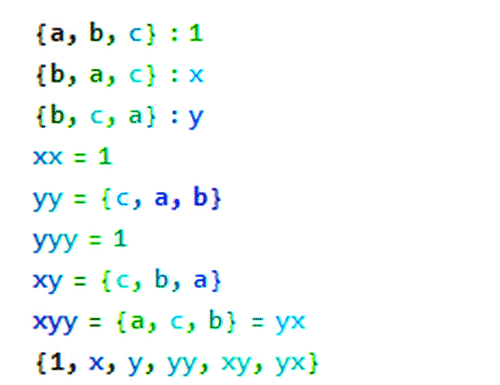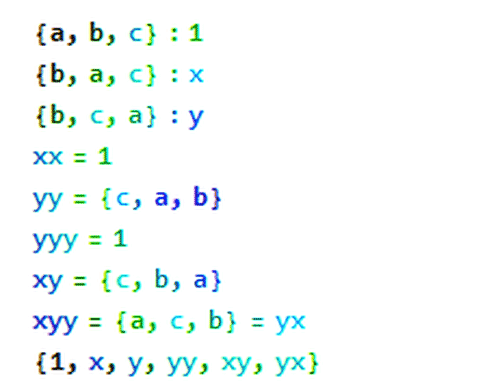
1、设u和v是S3里面的元素，u的逆元素是w，

那么v'=uvw就表示v的一个共轭。

比如，yy关于yx的共轭是y。

2、如果v遍历S3所有的元素，固定u为xy，那么所有关于u的共轭，就是S3的一个置换：

xy·{1, x, y, yy, xy, yx}·xy

注意，xy的逆元素是xy。

3、如果u遍历S3的所有元素，那么v的所有共轭，组成一个共轭类。

4、这样，我们可以把所有元素的共轭类写出来：

x的共轭类包括 {x, xy, yx}

y的共轭类包括 {y, yy}

yy的共轭类包括 {y, yy}

xy的共轭类包括 {x, xy, yx}

yx的共轭类包括 {x, xy, yx}

单位元的共轭类是{1}。

5、可以发现，共轭类只有三类：

{1}、 {y, yy}、{x, xy, yx}。

这是S3的一种分类方法。

类方程是指：

|S3| =|{1}| +|{y, yy}| +|{x, xy, yx}| 

6=1+2+3

不同的共轭类的元素数目之和，就是S3的元素数目。

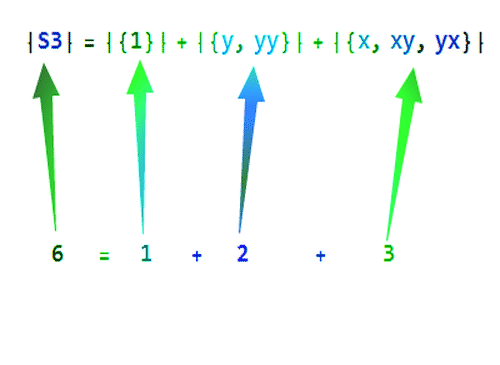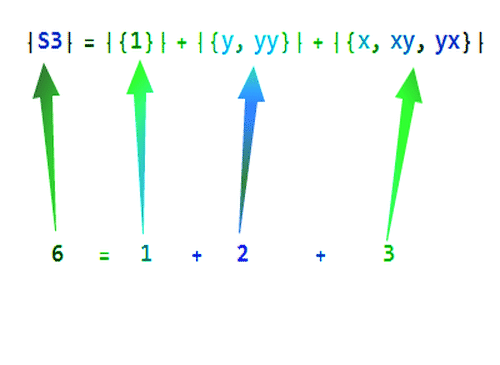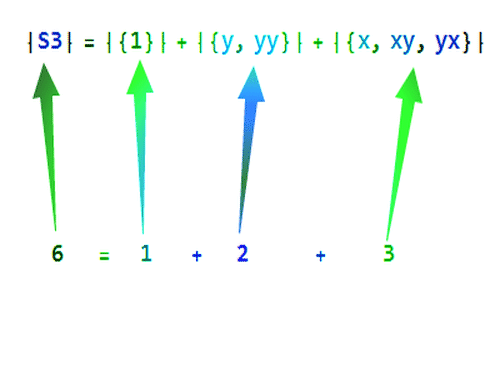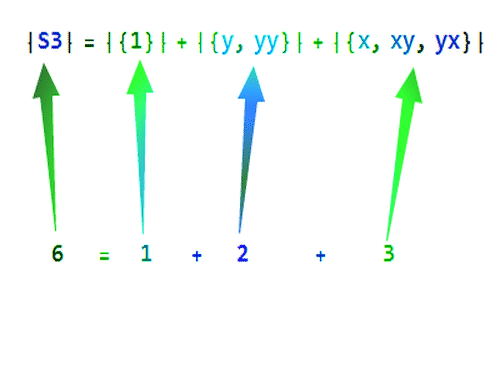
6、如果v关于u的共轭v'等于v，就说u属于v的中心化子。

比如，

x的中心化子是 {1, x}、

y的中心化子是 {1, y, yy}、

yy的中心化子是 {1, y, yy}、

xy的中心化子是 {1, xy}、

yx的中心化子是 {1, yx}。

7、注意，x的中心化子是{1, x}，x的共轭类是{x, xy, yx}，那么：

|S3| =|{1, x}| ·|{x, xy, yx}| 

6=2*3

其它元素都有类似公式。

8、单位元1的中心化子是S3的所有元素，它的共轭类是{1}。

这样，6=6*1

也是符合公式的。