网络流(c++)
1、一些简单的符号定义:
V表示整个图中的所有结点的集合.
E表示整个图中所有边的集合.
G = (V,E) ,表示整个图.
s表示网络的源点,t表示网络的汇点.
对于每条边(u,v),有一个容量c(u,v) (c(u,v)>=0)
如果c(u,v)=0,则表示(u,v)不存在在网络中。
如果原网络中不存在边(u,v),则令c(u,v)=0
对于每条边(u,v),有一个流量f(u,v).
2、网络流的三个性质:
1、容量限制: f[u,v]<=c[u,v]
2、反对称性:f[u,v] = - f[v,u]
3、流量平衡: 对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。
结合反对称性,流量平衡也可以写成下图的形式
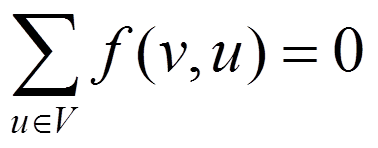
3、只要满足这三个性质,就是一个合法的网络流.
1、Luogu 3376&POJ 1273 Drainage Ditches
这两题是最大流,也就是最基本的网络流的最基本的题,初学者最好先写写这两题(我不会告诉你其实两题是一样的)
题目大意如下:
现在有m个池塘(从1到m开始编号,1为源点,m为汇点),及n条水渠,给出这n条水渠所连接的池塘和所能流过的水量,求水渠中所能流过的水的最大容量
其实你把这个池塘当做点,水渠当做边,就可以了,不过要注意两题在输入上有一些差别,洛谷的题有给源点和汇点,poj的题则没有,其实这不难,只要把洛谷3376的程序中s定义为1,t定义为m就可以了
2、洛谷3376程序 代码长度1.4kB 耗时818ms,这里用的是后面的网络流中很重要的一个dinic算法,它的做法先bfs求出bfs序,当要找增广路(可以增加的路径时),先判断这条边终点的bfs序是否等于起点的bfs序+1,如果是的话,再增广,否则,找另一条边
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <queue>
#include <string>
#include <algorithm>
using namespace std;
int n,m,s,t,u,v,w,e,dist[10005],x;
queue<int> q;
struct aa{
int to,w,next;
}edge[200005];//建边要用边表,要不然时间会爆
int head[10005],flow,maxflow;
bool add(int u,int to,int w)
{
edge[e].next=head[u];
edge[e].to=to;
edge[e].w=w;
head[u]=e++;
}//边表的建边操作,大家应该很熟悉,这里就不讲了
bool bfs()
{
memset(dist,0,sizeof(dist));//初始化
dist[s]=1;
q.push(s);
while(q.empty()==0)
{
int k=q.front();q.pop();
for(int i=head[k];~i;i=edge[i].next)
{
if(edge[i].w && !dist[edge[i].to])dist[edge[i].to]=dist[k]+1,q.push(edge[i].to);
}
}
return dist[t];//如果s和t不连通,则返回0
}//求每个点的bfs序
int dfs(int u,int flow)
{
if(u==t)return flow;//如果当前点=终点,终止循环
if(dist[u]>=dist[t])return 0;如果当前的的bfs序大于t的dfs序,则这不是一个合法的网络流,此时return 0
for(int i=head[u];~i;i=edge[i].next)
{
if(edge[i].w && dist[edge[i].to]==dist[u]+1 && (x=dfs(edge[i].to,min(edge[i].w,flow))))//如果这条边的权值>0 && 终点的bfs序大于起点的bfs序 && 这条边的终点能走到t,则执行
{
edge[i].w-=x;
edge[i^1].w+=x;//这步很重要,是所谓的加入后向边,防止这种策略错误,如果错误,还能原路走回来
return x;
}
}
return 0;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);//输入
memset(head,-1,sizeof(head));//初始化,这步很重要,我本来没加这步就wa了三个点
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);//输入
add(u,v,w);
add(v,u,0); //加边,记住网络流中正向的边和反向的边都要加,正向的按输入的权值加边,反向的按权值为0加边,记住,反向的边一定要加
}
while(bfs())//循环,当bfs()的结果不为0时,进入循环
{
while(x=dfs(s,1e9))//循环并且赋值,这个语句时将dfs(s,1e9)的值赋给x,并且进行判断,当x=0时跳出循环,否则,执行这个循环
{
maxflow+=x;累加答案
}
}
printf("%d\n",maxflow);输出
return 0;
}