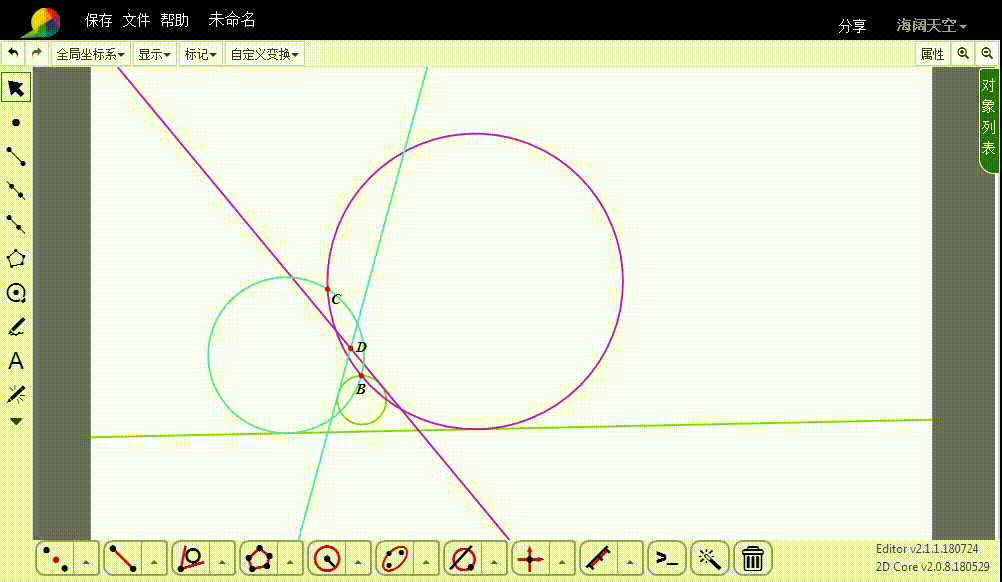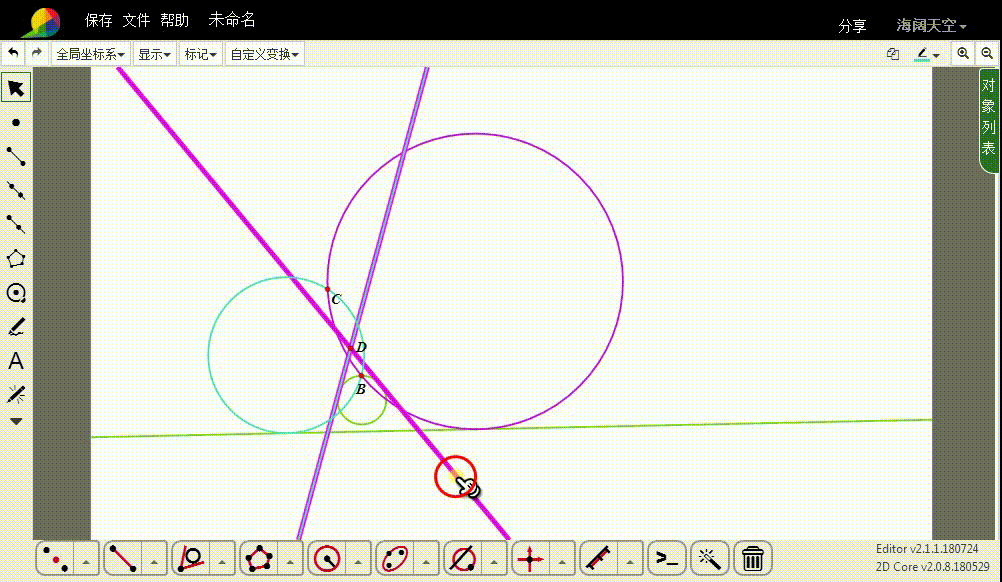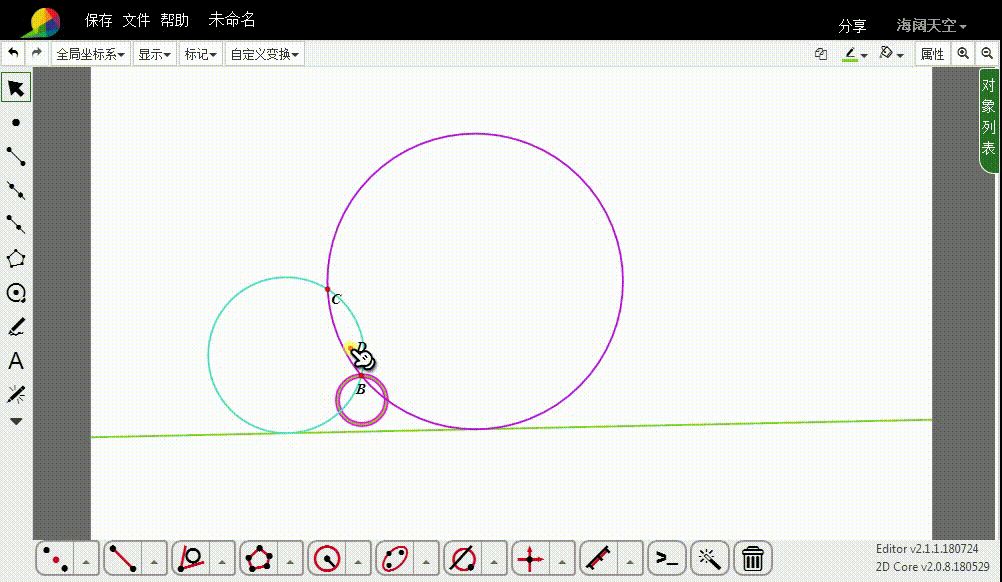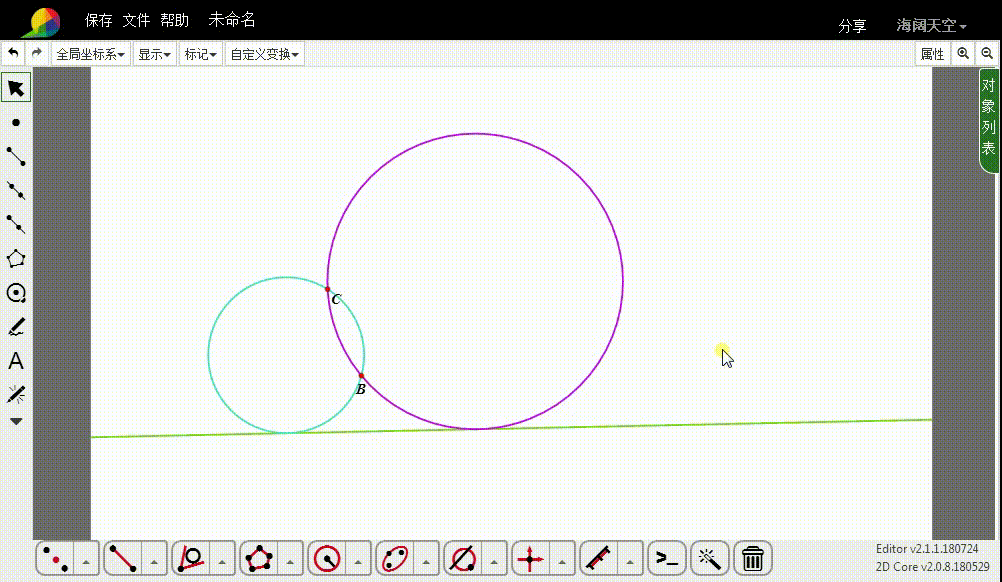
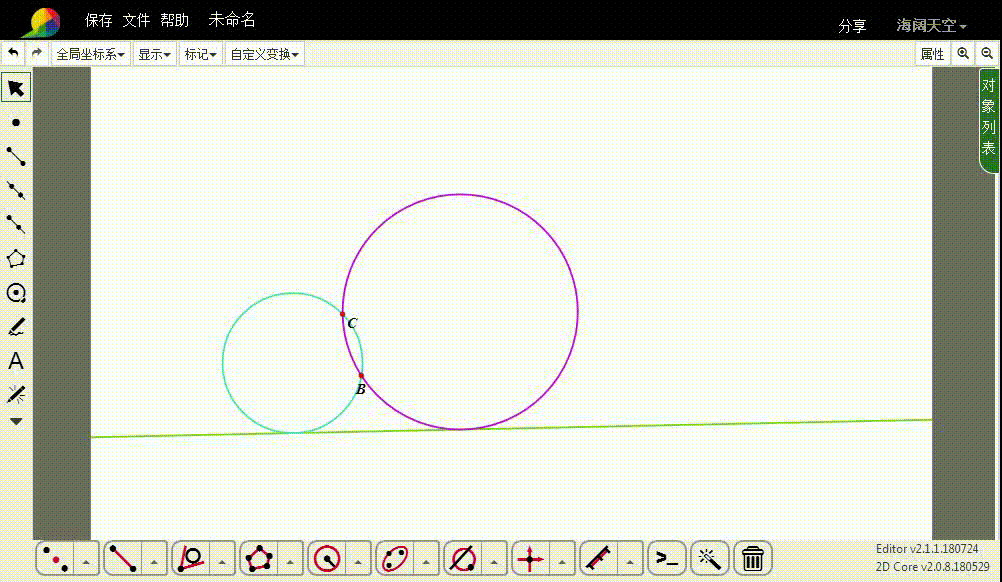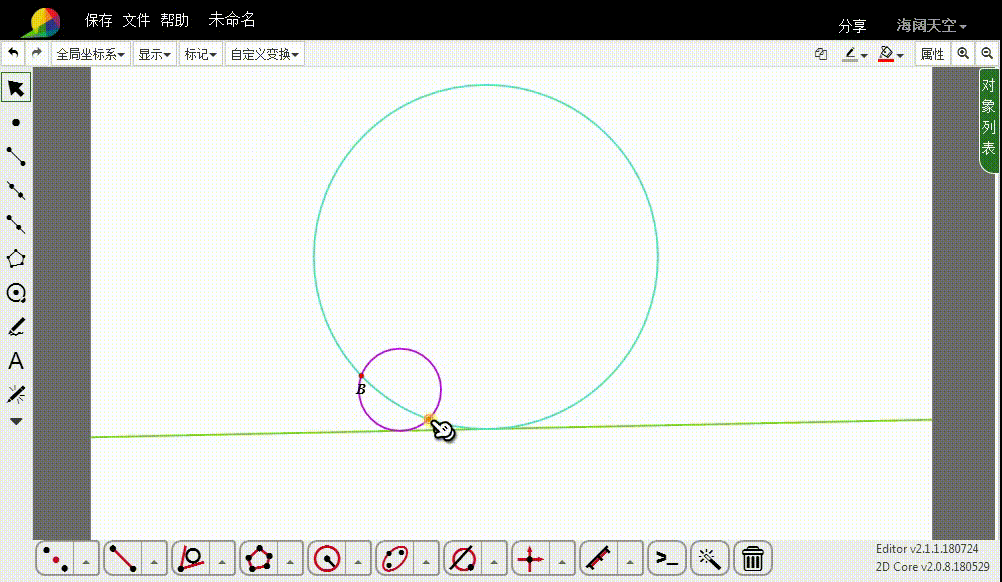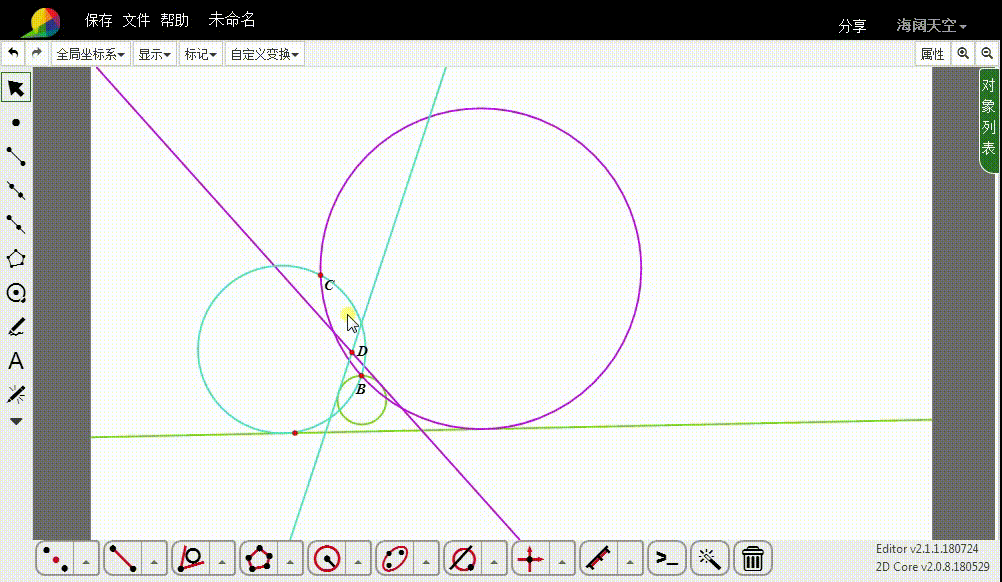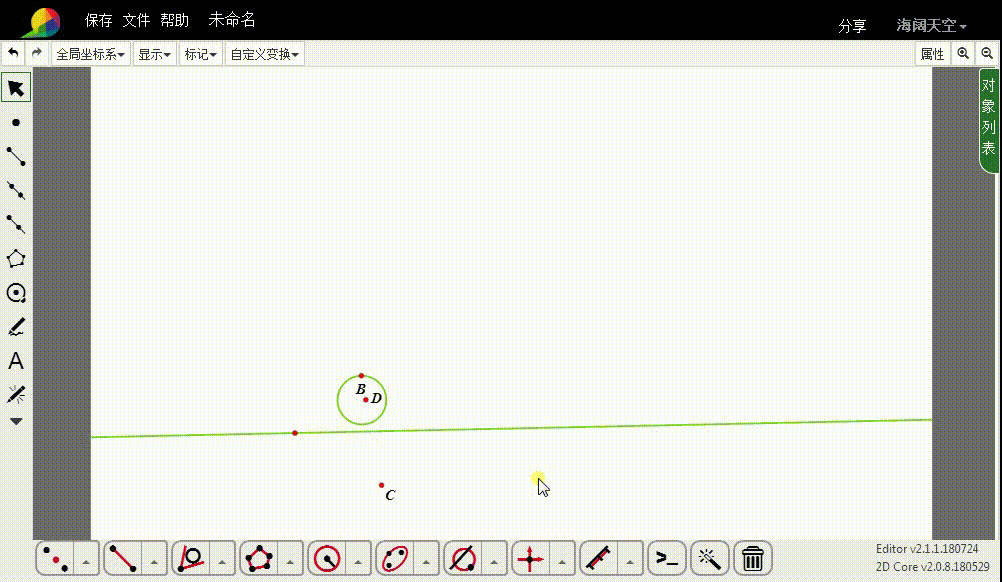
Apollonius问题——一线两点作切圆
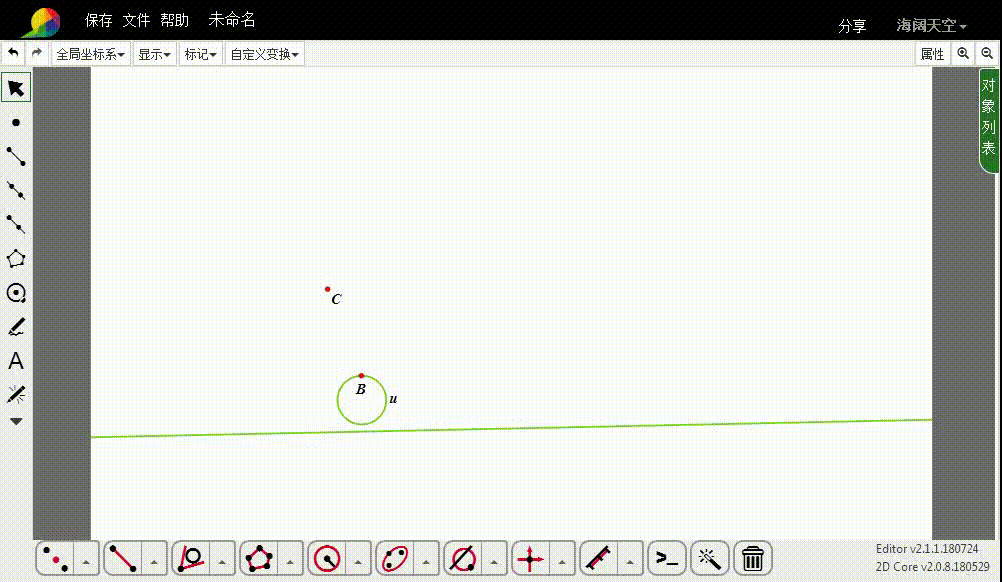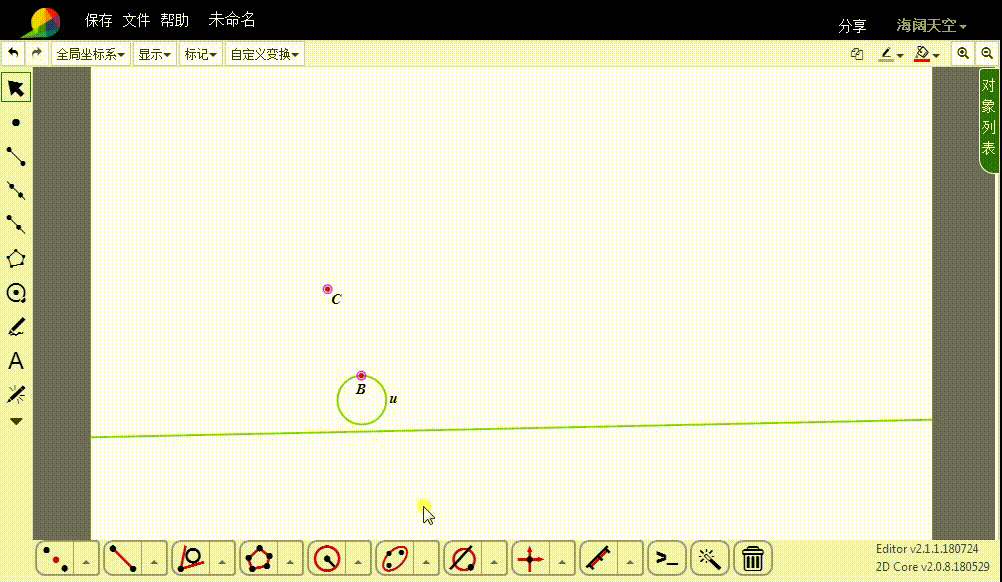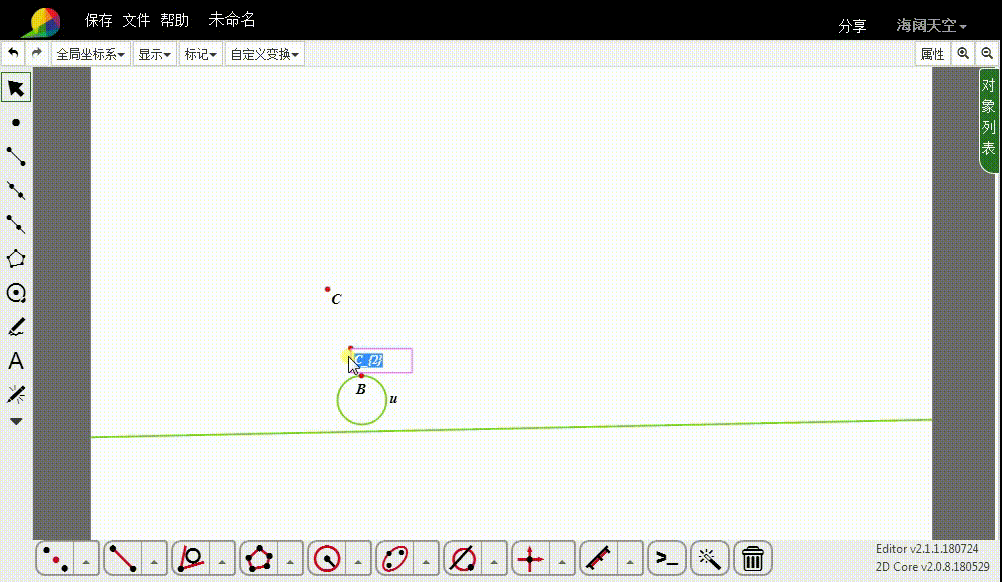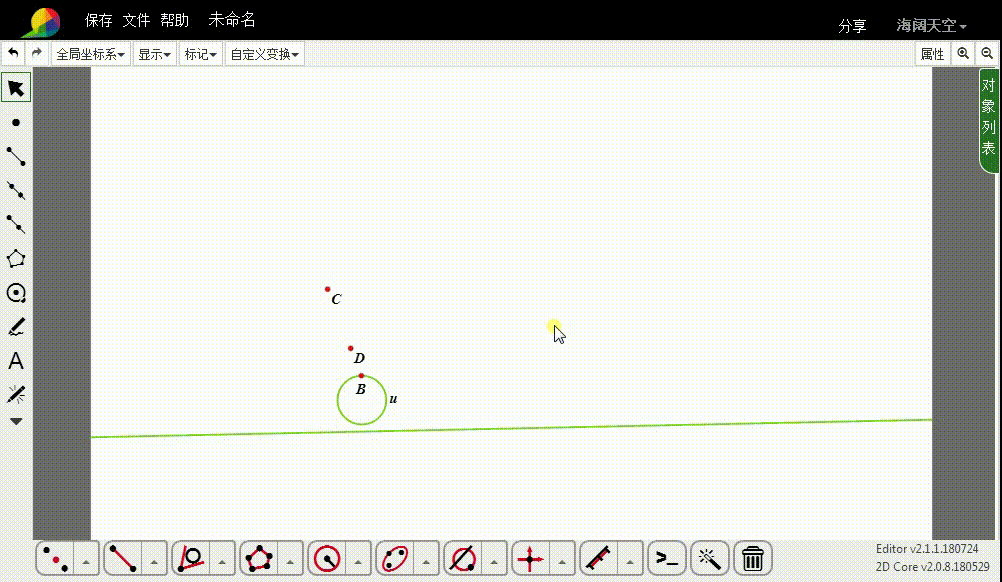
1、下面的整个作图,都以B为反演中心、1为反演率,进行反演变换。
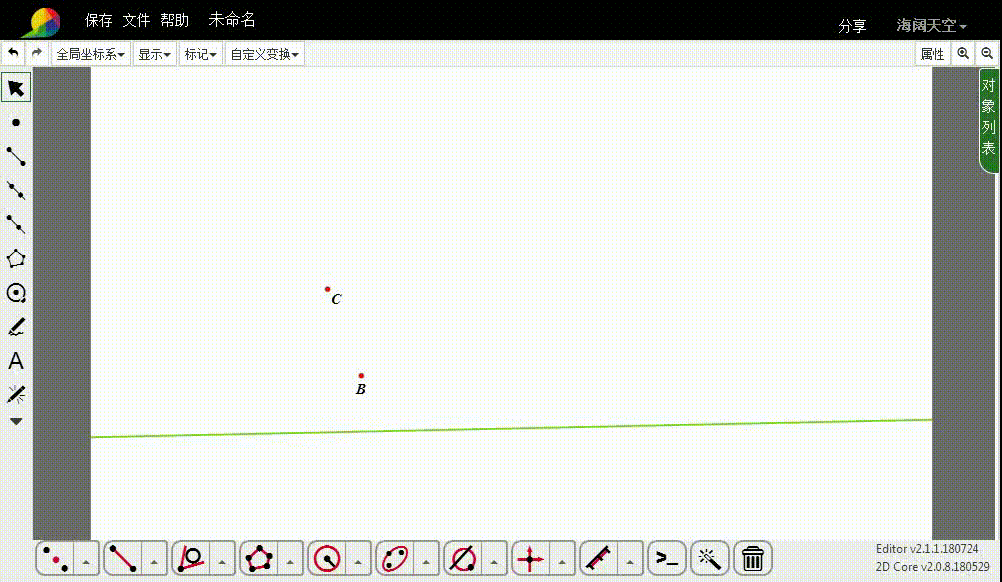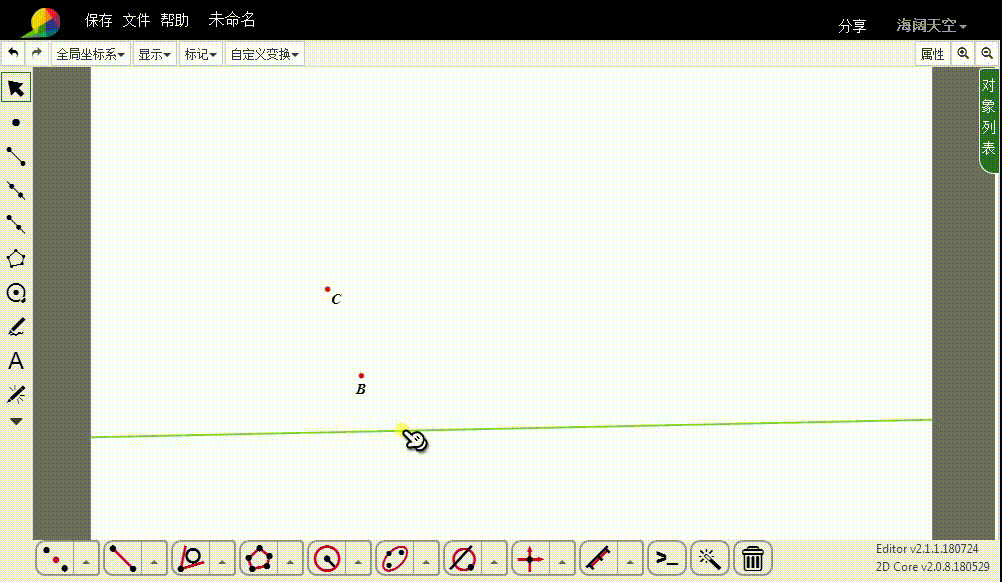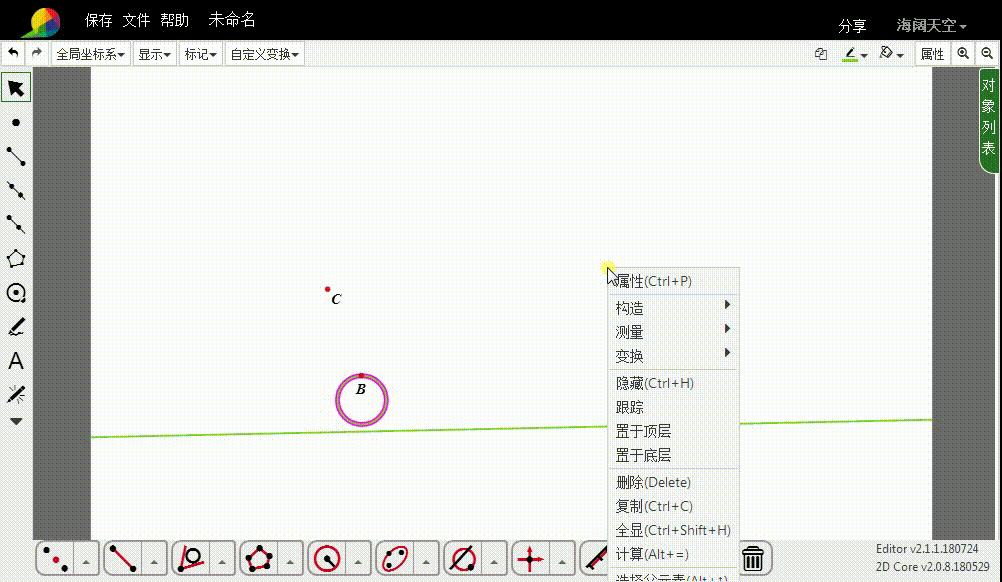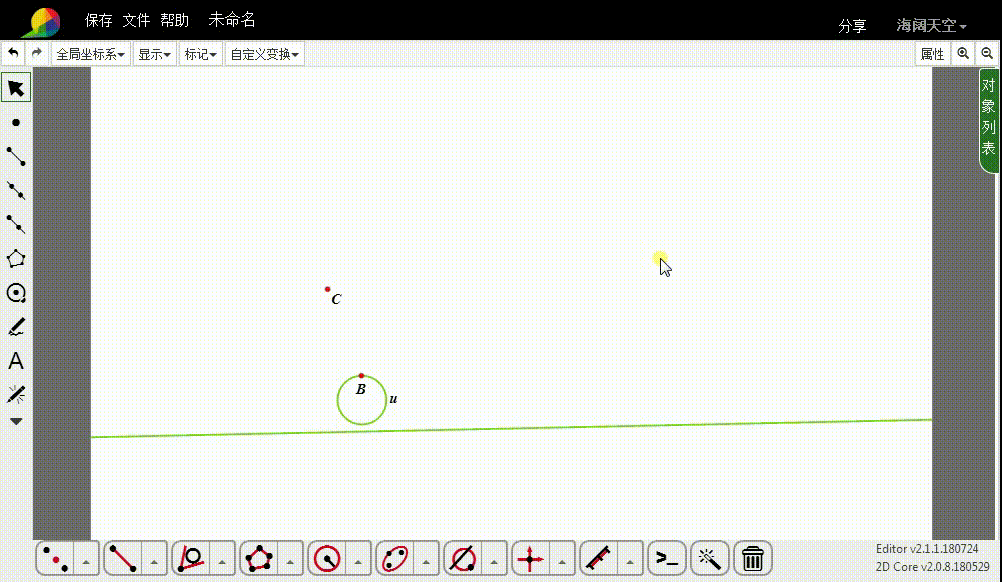
先作直线的反演图形,得到一个圆,记为u。
2、设C的反演点是D。
3、过D作圆u的切线,切线一般有两条。
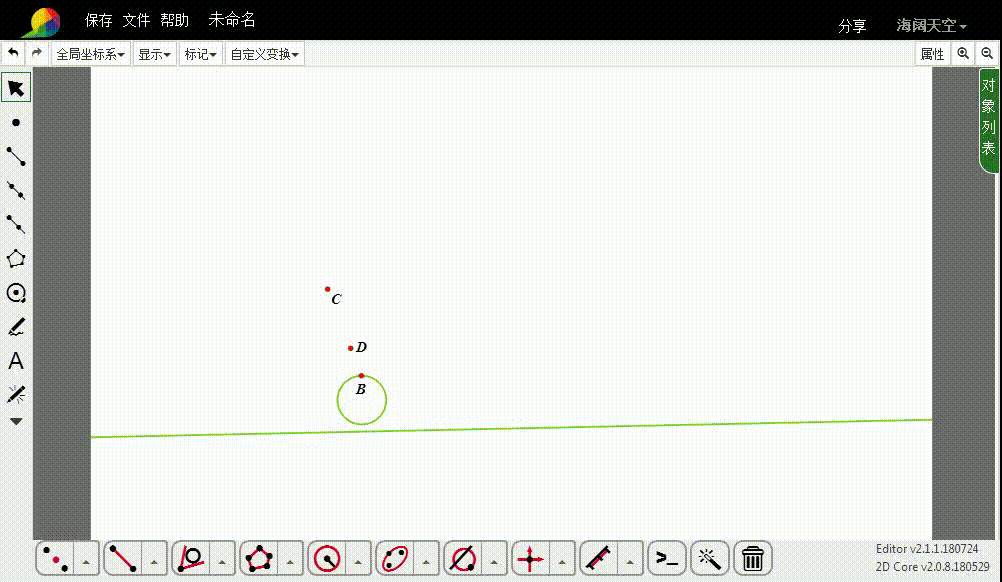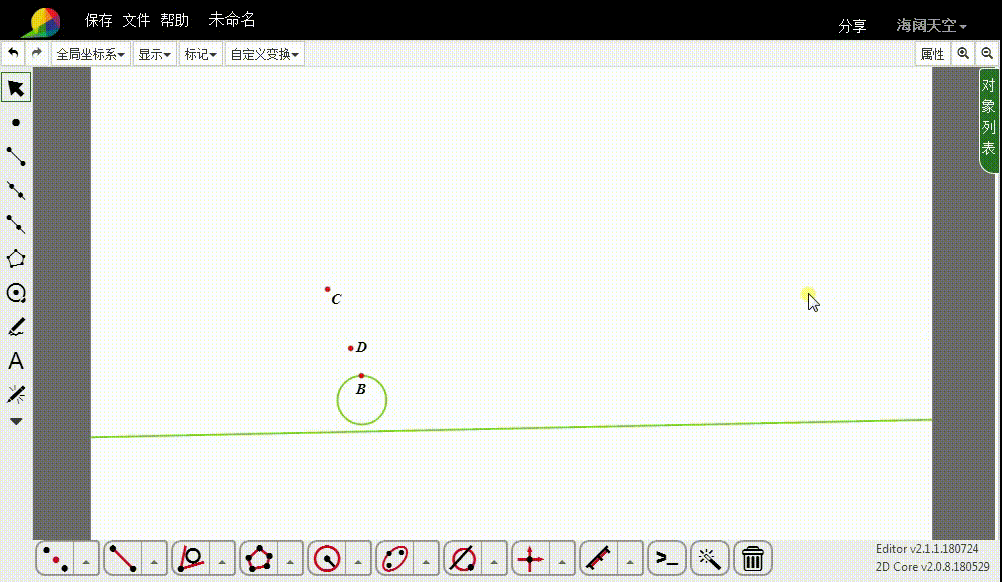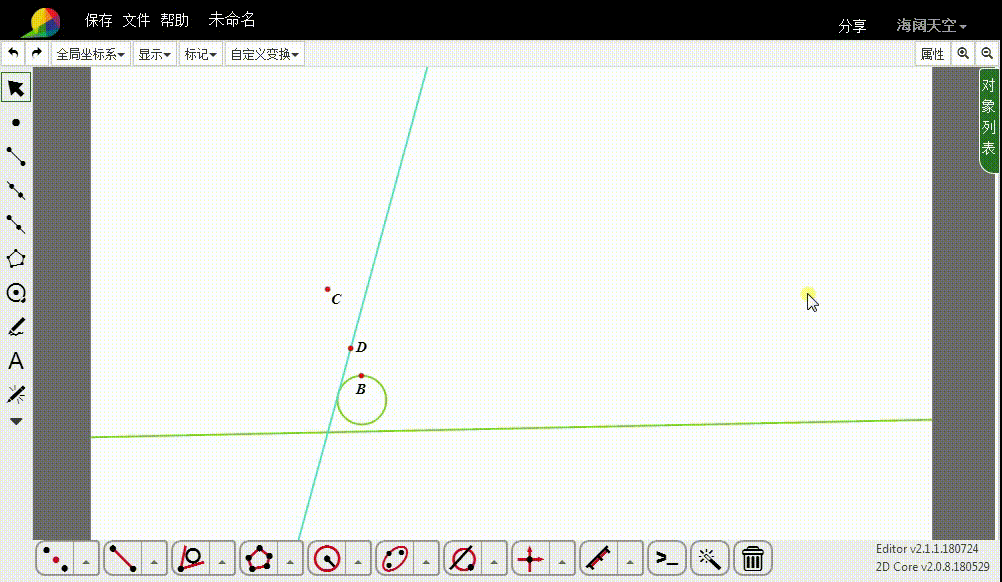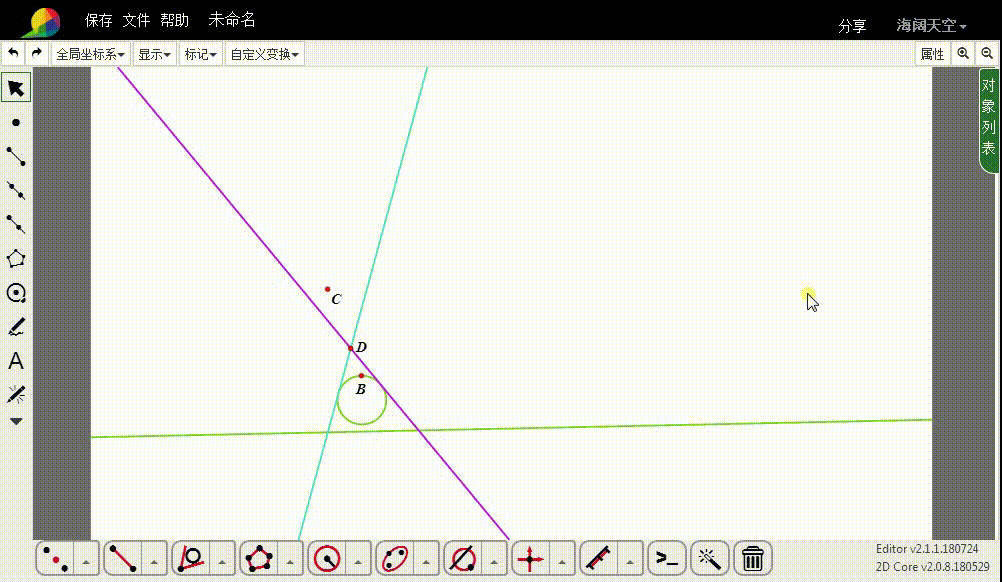
4、这两条切线的反演图形,就是所要求作的圆。
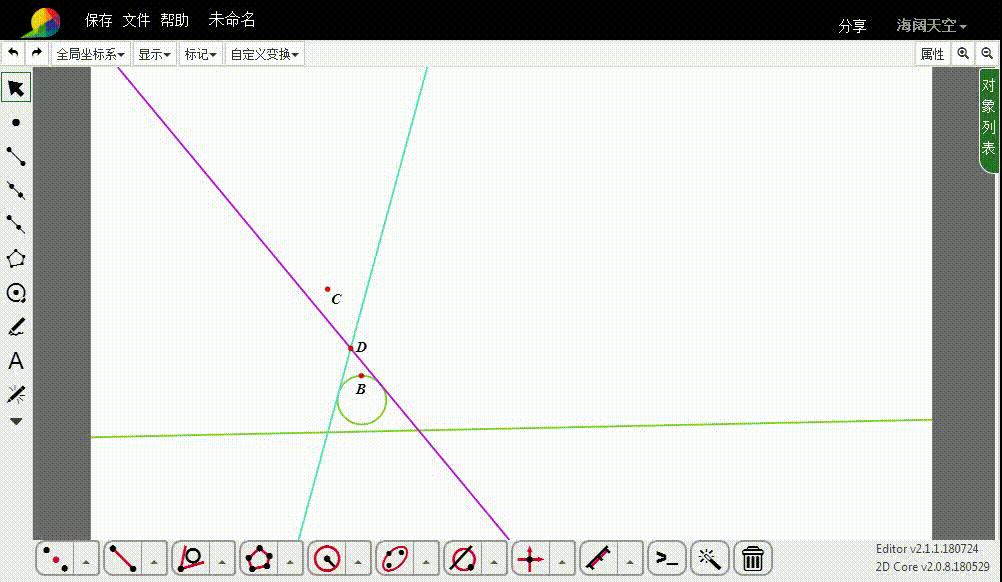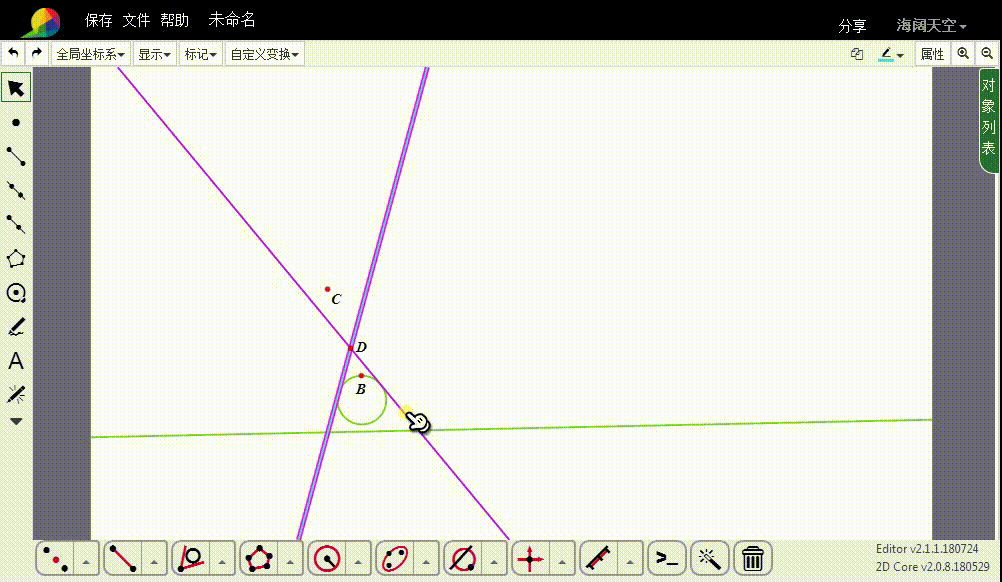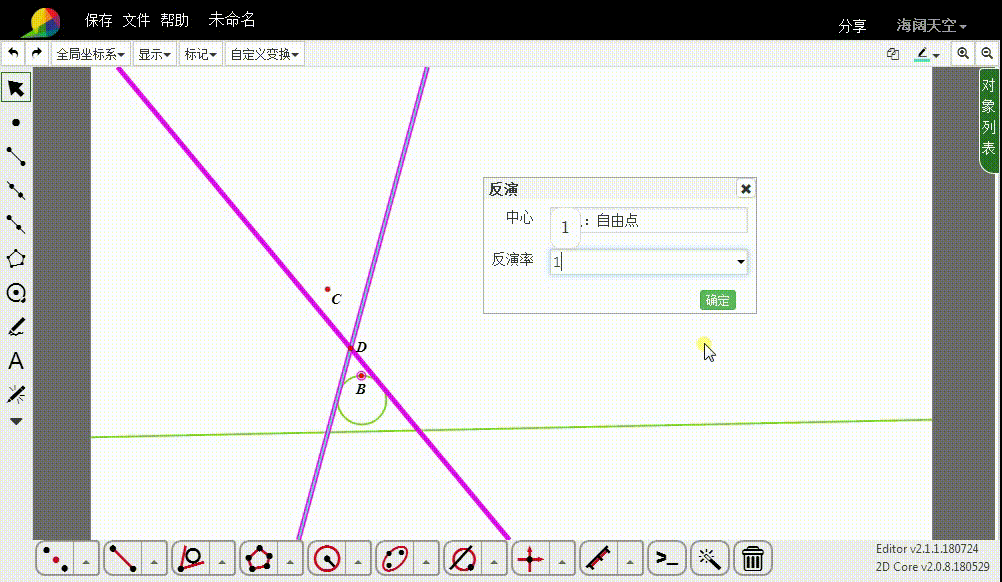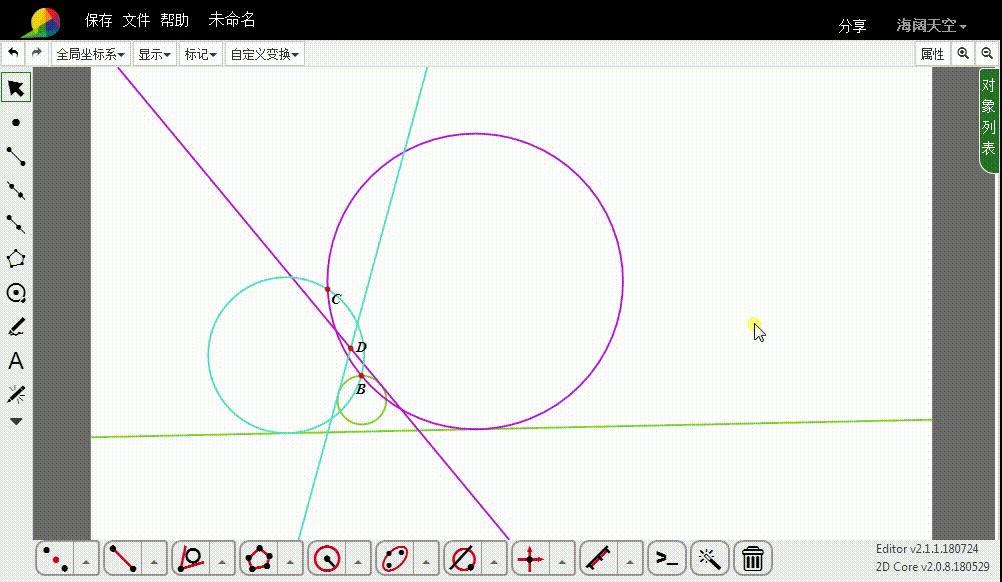
5、隐藏多余的图形。
6、当BC的连线与给定的直线平行的时候,其中的一个切圆变成了与给定直线平行的线。
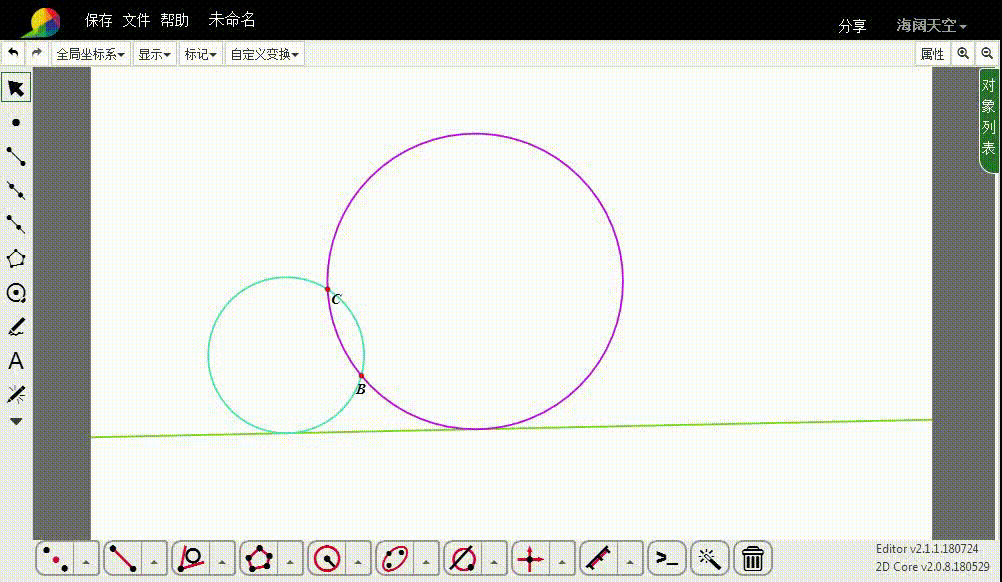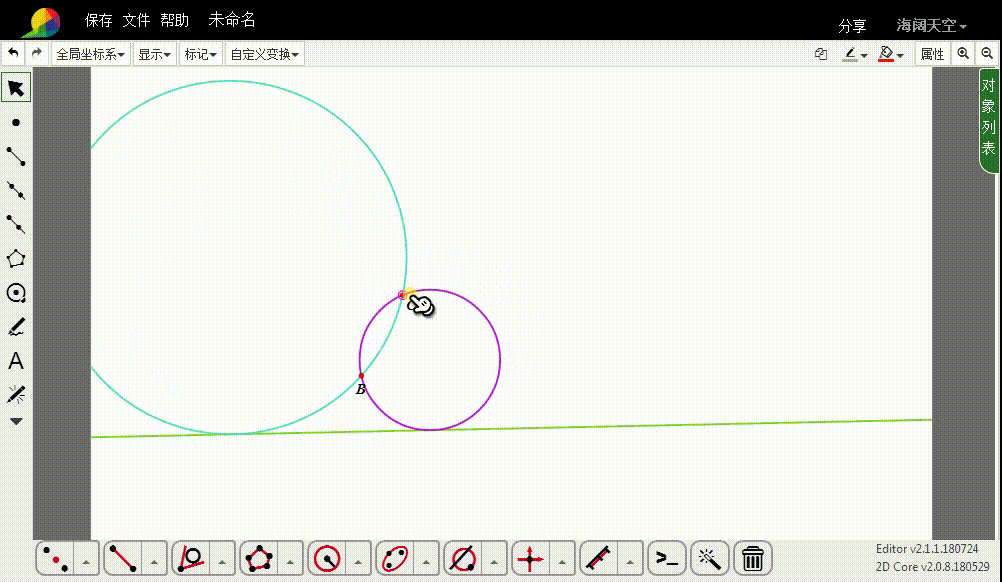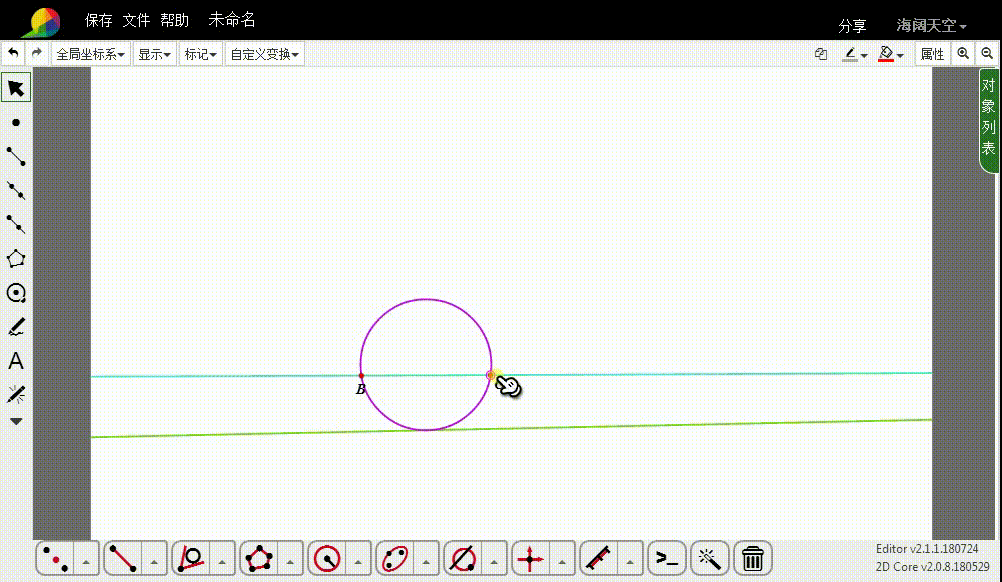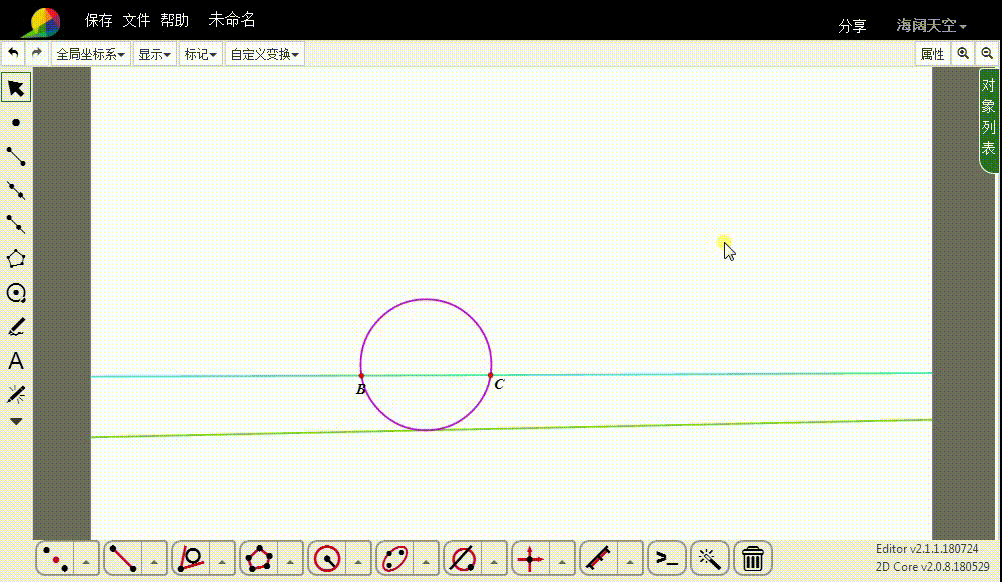
7、当B和C位于给定的直线两侧的时候,两个切圆消失了。这是怎么回事?
原因是,D跑到了圆u的内部,切线不存在了,自然的,切线的反演图形也不存在了。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:21
阅读量:49
阅读量:24
阅读量:43
阅读量:161