小波变换图像处理
1、wavedec2函数用于对图像进行二维小波分解,其函数调用格式如下:
[c,l]=wavedec2(X,n,’wname’);
其中,X表示原始图像,n表示分解层数,wname表示小波函数,c表示各层系数,l表示各层系数对应的长度
ddencmp用于得到全局阀值,其调用格式如下:
[thr,sorh,keepapp]=ddencmp(‘cmp’,’wp’,X);
[thr,sorh,keepapp]=ddencmp(‘cmp’,’wv’,X);
其中cmp表示压缩,wp表示小波包,wv表示小波,X表示原始信号,thr表示阀值,sorh表示阀值类型,s表示软阀值,h表示硬阀值,keepapp=1表示保持近似系数不变
wdencmp用于对数据或图像进行阀值去噪或压缩,其调用格式如下:
[xcomp,c1,l1,perf0,perfl2]=wdencmp(‘gbl’,c,l,’wname’,n,thr,sorh,keepapp);
glb表示利用全局阀值,perf0表示恢复比,perfl2表示压缩比
示例:利用二维小波对图像进行压缩
编写对应的m文件如下:
clc;
load woman;
subplot(1,2,1)
imshow(X,map);
title('原始图像');
[c,l]=wavedec2(X,3,'sym4');
%%获取全局阀值%%
[thr,sorh,keepapp]=ddencmp('cmp','wp',X);
[xcmp,c1,l1,perf0,perfl2]=wdencmp('gbl',c,l,'sym4',3,thr,sorh,keepapp);
subplot(1,2,2)
imshow(xcmp,map);
title('压缩后图片');
程序运行结果如下图:

2、小波变换用与图像去噪,噪声会影响图像处理的输入,采集,处理的各个环节及输出结果等全过程,因此对于图像的噪声处理是一个不可忽略的重要的问题,去噪已经成为图像处理中不可或缺的一部分
示例:对图像进行二维小波去噪
编写对应的m文件如下:
load julia;
%%产生噪声信号%%
init=3718025452;
rand('seed',init);
xnoise=X+8*rand(size(X));
colormap(map);
subplot(1,3,1)
imshow(X,map);
title('原始信号')
subplot(1,3,2)
imshow(xnoise,map);
title('含有噪声的信号');
%%获取全局阀值%%
[thr,sorh,keepapp]=ddencmp('den','wp',xnoise);
[xden,c1,l1]=wdencmp('gbl',xnoise,'sym4',3,thr,sorh,keepapp);
subplot(1,3,3)
imshow(xden,map);
title('去除噪声后信号');
程序运行结果如下图:

3、小波分析用于图像增强,图像增强是对图像进行一定处理,使图像比原图更加清晰,视觉效果更好。
示例:利用小波分析对图像进行增强
编写对应的m文件如下:
clc;
load facets;
subplot(1,2,1)
imshow(X,map);
title('原始信号');
[c,l]=wavedec2(X,3,'sym4');
sizec=size(c);
for i=1:sizec(2)
if(c(i)>250)
c(i)=2*c(i);
else
c(i)=0.5*c(i);
end
end
y=waverec2(c,l,'sym4');
subplot(1,2,2)
imshow(y,map);
title('增强图像');
程序运行结果如下图:

4、图像钝化
图像的钝化可以在时域中,也可以在频域中,在时域中处理较为简单,只需要加一个平滑滤波器,使图像中每个点与其邻点做平滑处理即可,在此主要说明图像钝化在频域中的处理。图像钝化是为了突出低频信息,弱化高频信息。
示例:对图像进行频域钝化处理,
编写对应的m文件如下:
load chess;
subplot(1,2,1)
imshow(X,map);
title('原始图像');
[c,l]=wavedec2(X,3,'db4');
sizec=size(c);
for i=1:sizec(2)
if(c(i)>280)
c(i)=c(i)*2;
else
c(i)=c(i)*0.5;
end
end
y=waverec2(c,l,'db4');
subplot(1,2,2)
imshow(y,map);
title('采用小波方法钝化图像');
程序运行结果如下图:

5、图像锐化,与图像钝化刚好相反,是为了突出高频信息,弱化低频信息,从快速变化的成分中分离出系统边界成分,以便进一步识别或者分割等操作。
示例:对图像进行锐化处理
编写对应的m文件如下:
load chess;
subplot(1,2,1)
imshow(X,map);
title('原始图像');
[c,l]=wavedec2(X,3,'db5');
sizec=size(c);
%%突出高频信息,弱化低频信息%%
for i=1:sizec(2)
if(abs(c(i))<280)
c(i)=c(i)*2;
else
c(i)=c(i)*0.5;
end
end
y=waverec2(c,l,'db5');
subplot(1,2,2)
imshow(y,map);
title('采用小波方法锐化图像');
程序运行结果如下图:

6、小波分析用于图像融合
图像融合是将同一图像的两个部分或者不同图像合成一张图,以便合成之后的图形比原来更容易理解。
示例:利用二维小波变换将两幅图像融合在一起
编写对应的m文件如下:
clear all;
load bust;
X1=X;
map1=map;
load woman;
X2=X;
map2=map;
subplot(1,3,1)
imshow(X1,map1);
title('第一幅图像');
subplot(1,3,2)
imshow(X2,map2);
title('第二幅图像');
%%对第二幅图形低频部分和高频部分进行处理%%
for i=1:256
for j=1:256
if (X2(i,j)>120)
X2(i,j)=X2(i,j)*2;
else
X2(i,j)=X2(i,j)*0.5;
end
end
end
[c1,l1]=wavedec2(X1,3,'sym4');
[c2,l2]=wavedec2(X2,3,'sym4');
%%对图像进行融合%%
c=c1+c2;
%%减少图像的亮度%%
c=c*0.5;
y=waverec2(c,l1,'sym4');
subplot(1,3,3)
imshow(y,map2);
title('融合后图像');
程序运行结果如下图:

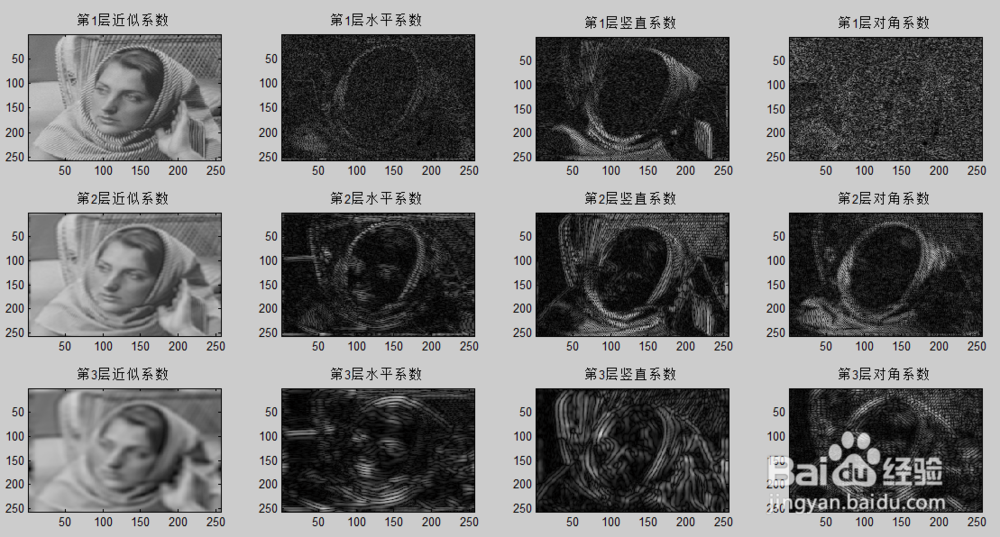
7、小波分析用于图像分解
对图像分解的目地在于可以更好的观察图像的细节,对图像做出更好的判断,swt2函数用于对图像进行分解,其调用格式如下:
[sa,sh,sv,sd]=swt2(X,N,’wname’);
其中sa,sh,sv,sd分别表示近似系数,水平系数,竖直系数,对角系数,x分解图像,N分解的层数,wname表示小波基名称
示例:对图像进行分解
编写对应的m文件如下:
clear all;
load woman;
[sa,sh,sv,sd]=swt2(X,3,'db3');
s=1;
for i=1:3
subplot(3,4,s)
image(wcodemat(sa(:,:,i),192));
title(['第',num2str(i),'层近似系数']);
subplot(3,4,s+1)
image(wcodemat(sh(:,:,i),192));
title(['第',num2str(i),'层水平系数']);
subplot(3,4,s+2)
image(wcodemat(sv(:,:,i),192));
title(['第',num2str(i),'层竖直系数']);
subplot(3,4,s+3)
image(wcodemat(sd(:,:,i),192));
title(['第',num2str(i),'层对角系数']);
s=s+4;
end
程序运行结果如下图: