四元数群的正规子群、中心、中心化子

1、四元数群的二阶子群是正规子群。

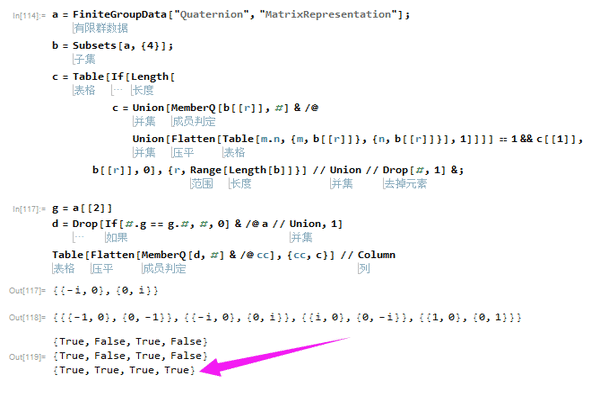
通过下面的代码可以证明。

2、四元数群的三个4阶子群，都是正规子群。

3、这样就可以断言，四元数群的所有子群都是正规子群。

1、群的中心，指的是可与所有群元素交换的元素的集合。

四元数群的四阶子群，都不是群的中心。

2、四元数群的唯一的二阶子群，恰好符合群的中心的定义。

3、这样就可以断言，四元数群的中心，必定是那唯一的二阶子群。

1、给定G的元素g，能够和g交换的G的元素的集合，称为g关于G的中心化子。

G的单位元的中心化子是G。

2、{{-I, 0}, {0, I}}关于四元数群的中心化子是一个四阶子群：

{{{-1, 0}, {0, -1}}, {{-I, 0}, {0, I}}, {{I, 0}, {0, -I}}, {{1, 0}, {0, 1}}}

3、{{0, 1}, {-1, 0}}的中心化子是另一个四阶子群：

{{{-1, 0}, {0, -1}}, {{0, -1}, {1, 0}}, {{0, 1}, {-1, 0}}, {{1, 0}, {0, 1}}}

4、以{{{1, 0}, {0, 1}}, {{0, -I}, {-I, 0}}, {{-1, 0}, {0, -1}}, {{0, I}, {I, 0}}}为中心化子的元素是{{0, -I}, {-I, 0}}或 {{0, I}, {I, 0}}；

以{{{1, 0}, {0, 1}}, {{0, 1}, {-1, 0}}, {{-1, 0}, {0, -1}}, {{0, -1}, {1, 0}}}为中心化子的元素是{{0, -1}, {1, 0}}或{{0, 1}, {-1, 0}}；

以{{{1, 0}, {0, 1}}, {{-I, 0}, {0, I}}, {{-1, 0}, {0, -1}}, {{I, 0}, {0, -I}}}为中心化子的元素是{{-I, 0}, {0, I}}或 {{I, 0}, {0, -I}}。

这三个中心化子恰好是四元数群的三个四阶子群

5、{{{1, 0}, {0, 1}}, {{-1, 0}, {0, -1}}}是四元数群唯一的二阶子群，以它为中心化子的集合是：

{{{0, -1}, {1, 0}}, {{0, -I}, {-I, 0}}, {{0, I}, {I, 0}},

  {{0, 1}, {-1, 0}}, {{-I, 0}, {0, I}}, {{I, 0}, {0, -I}}}

？？？这个集合里面为什么没有单位元？