平面上点集的分类——用映射确定等价关系

1、如果映射是：f(x,y)=x^6+y^6，

那么f=1，确定了一类点集，它们构成一条曲线。

2、如果按照f>1、=1、<1来分类，那么平面上的点就可以分为三类。

3、如果按照f取不同的正数值来划分，那么平面上的点可以划分为无数类。

4、还可以按照正整数区间来划分：

当0≤f＜2，为一类点；

当当2≤f＜4，为一类点；

……

也有无数类。

1、再试试另一个映射：

h(x,y)=abs(x^9)+abs(y^3)，

那么可以取不同的正值，来对平面点集进行分类。

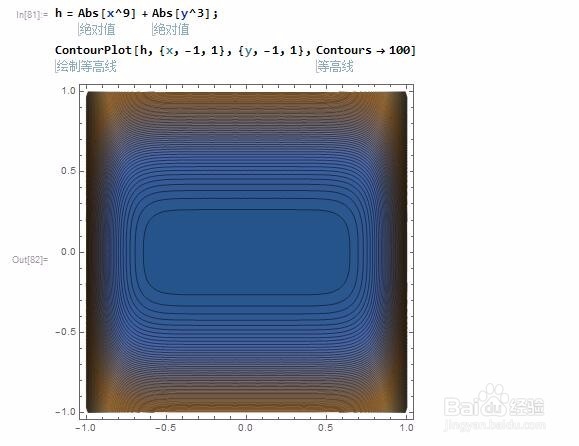
2、下图里面的两个点，都使得h等于1/3，所以在这个意义上说，它们是一类的。

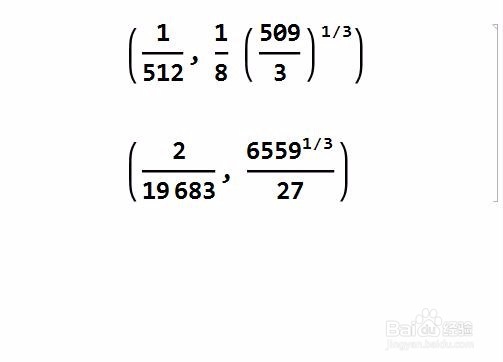
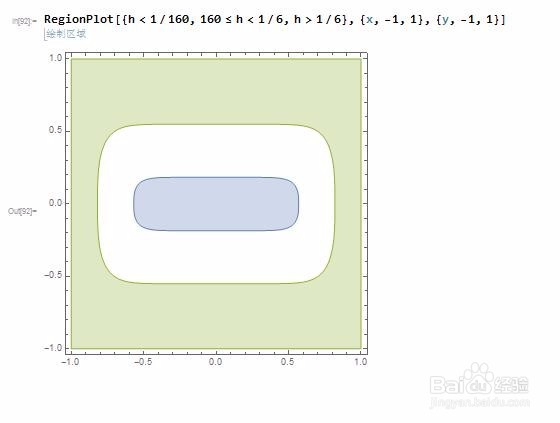
3、如果要把平面上的点分为3类，一般就是：

边界上的点、内部的点、外部的点。