【平面几何】含60°角的三角形问题之二

1、先固定坐标系：

C为原点，A在x轴正半轴上，B在第一象限内部；

坐标依次是：

CC = {0, 0}; A = {a, 0}; B = b*ReIm[E^(Pi/3*I)]; P = {m, n};

CC就是C点，a、b、m、n都大于零。

2、然后，根据要求列方程组，解方程组：

sol = Solve[{ju[CC, P] == 10,

    ju[A, P] == 6,

    ju[B, P] == 7,

    ju[A, B] == 13,

    a > 0, b > 0, m > 0, n > 0}, {a, b, m, n}] // FullSimplify

其中，ju[X,Y]代表点X和点Y之间的距离。

3、有两组解，就说明满足要求的△ABC有两个。

分别计算出这两个三角形的边长AC和BC：

{ju[A, CC], ju[B, CC]} /. sol // FullSimplify

4、画出第一种情形：

5、画出第二种情形：

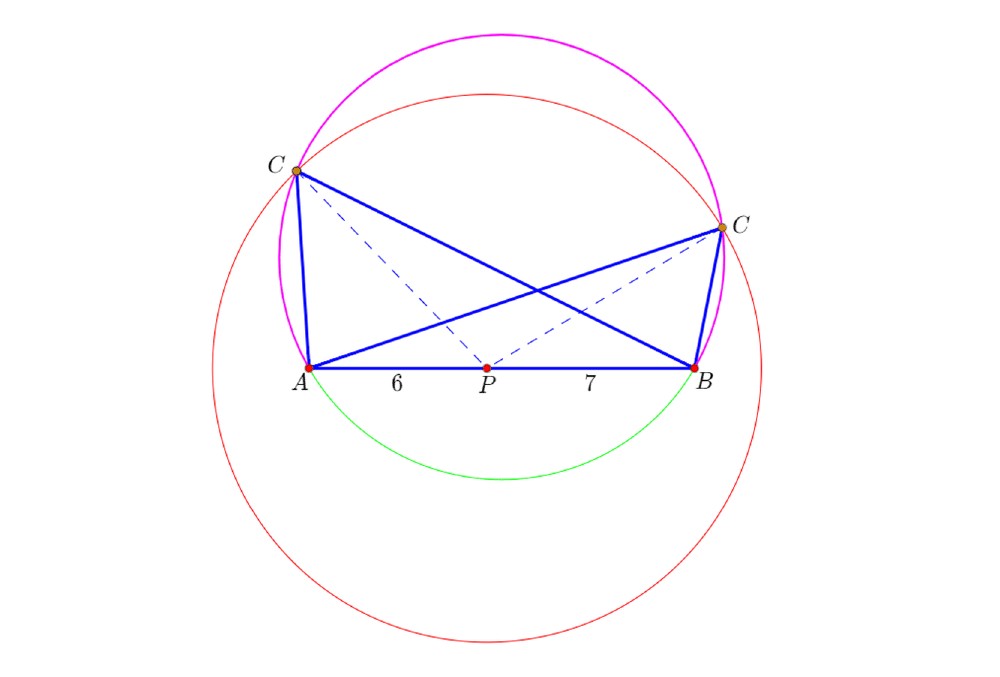
6、把这两种情形画在一起：

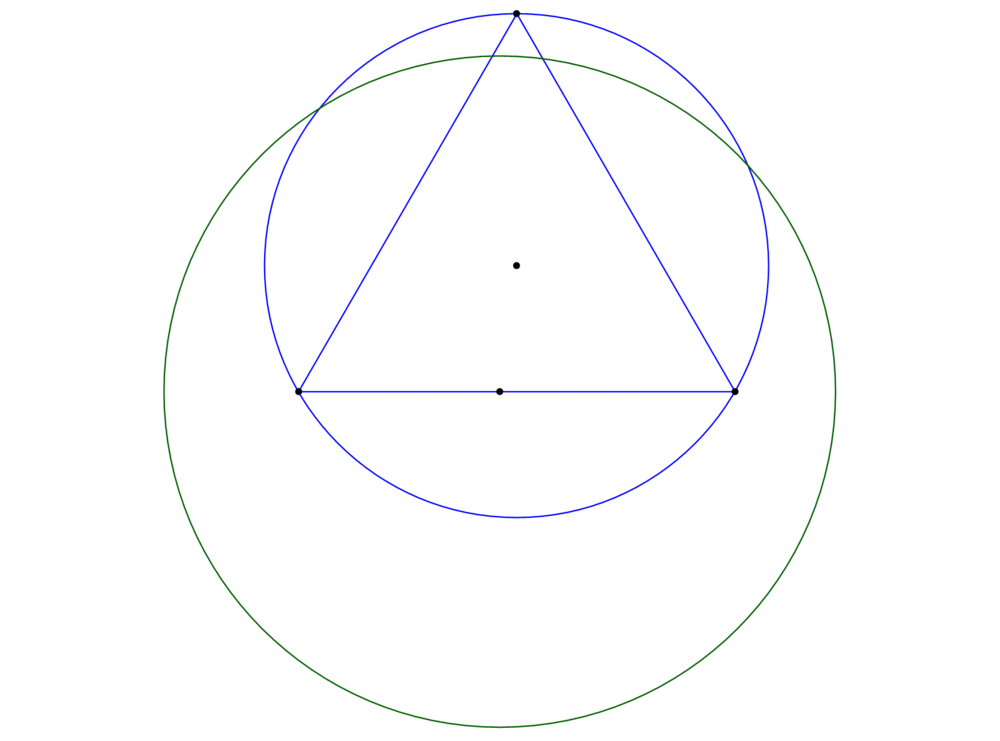
7、还有另一种画图方法，就是固定ABP三点，反过来确定C的两个位置：

以AB为一边的正三角形的外接圆（图中蓝色圆）；

以P为圆心、10为半径的圆（图中绿色圆）；

这两个圆有两个交点，就代表C点的两个位置。

1、此时要考虑的问题是：

△ABC，∠ACB=60°，P是线段AB之间的点，AP=6，BP=7，求CP的取值范围。

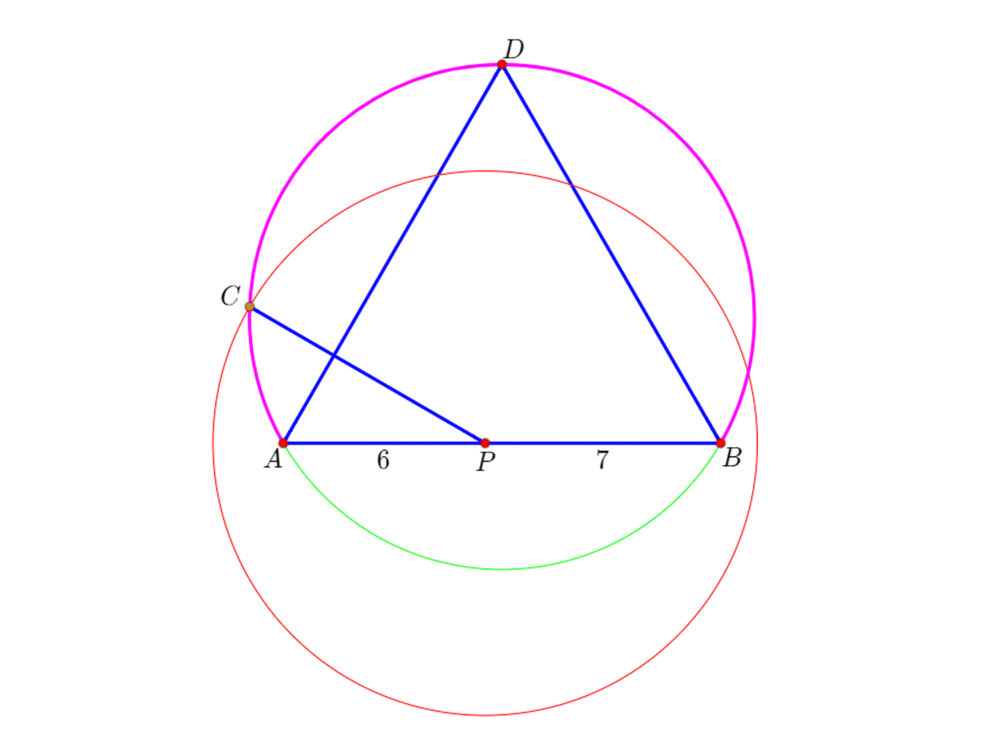
2、作正三角形ABD，以及三点弧ADB；

以P为圆心、PC为半径的圆，需要与三点弧ADB有交点（异于A和B的点）；

由此可知，PC必须大于6。

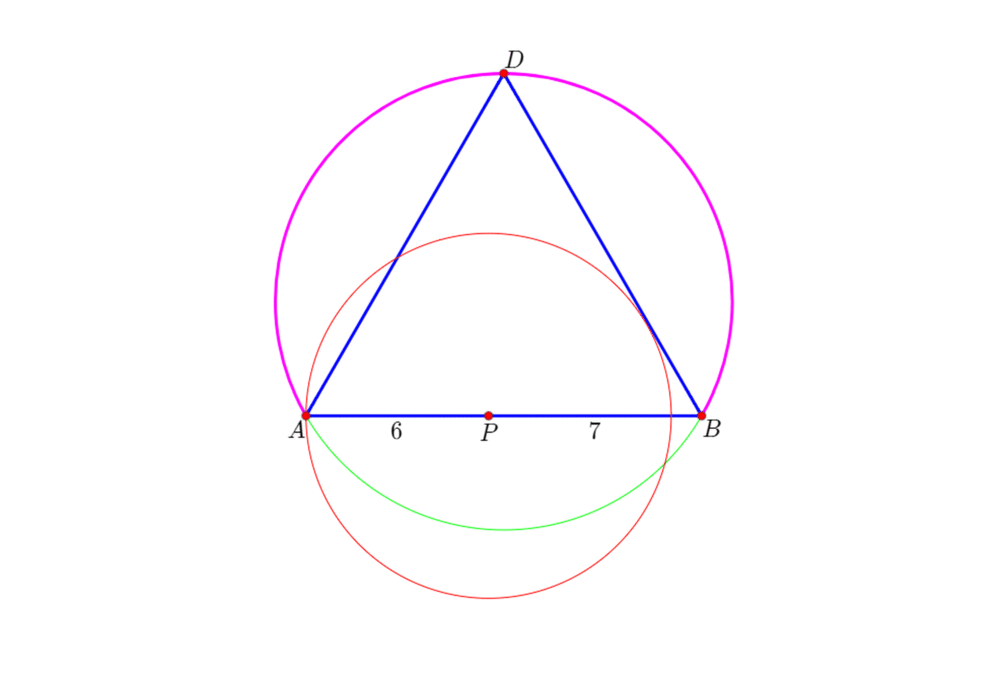
3、当6<PC≤7的时候，满足要求的△ABC是唯一确定的。

注意，这里指的是形状唯一。

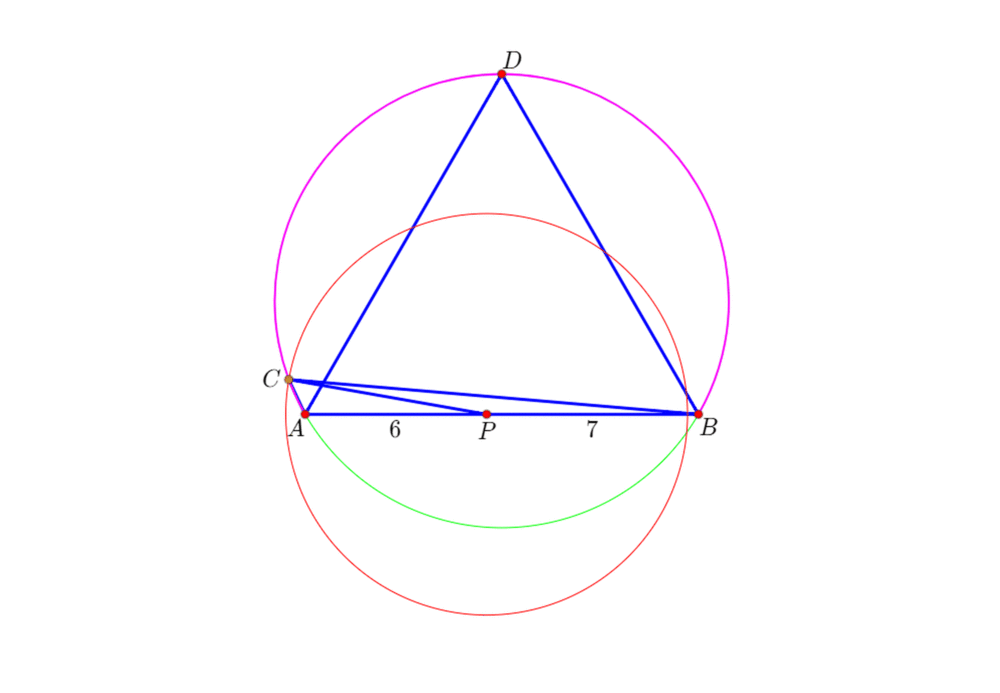
4、PC的最大值是(13 + sqrt(43))/sqrt(3)，此时圆P与三点弧ADB相切。

这时候，△ABC的形状也是唯一确定的。

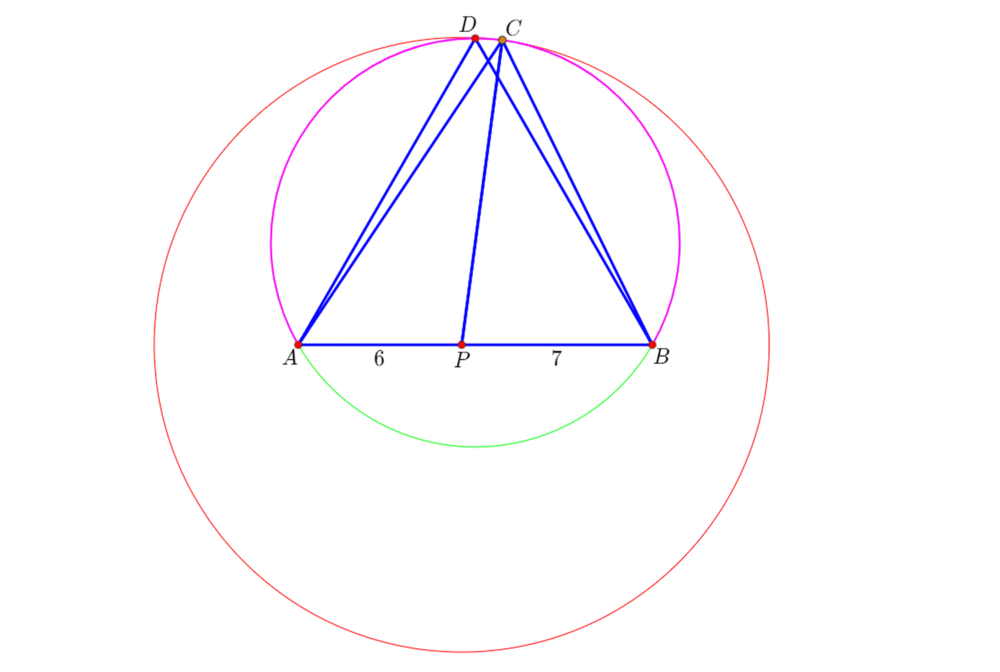
5、当PC的长度介于7和(13 + sqrt(43))/sqrt(3)（约等于11.2915）之间的时候，△ABC的形状是唯二确定的。