用网络画板演示复平面上z→sin(sin(z))的变换
1、构造变量n,保持为最小值0。

2、构造直角坐标点A,横坐标是n-1,纵坐标是-1。
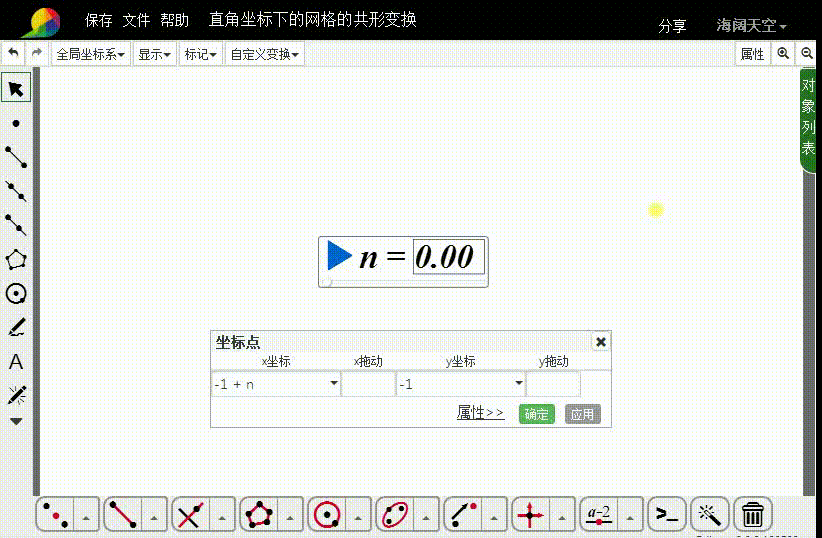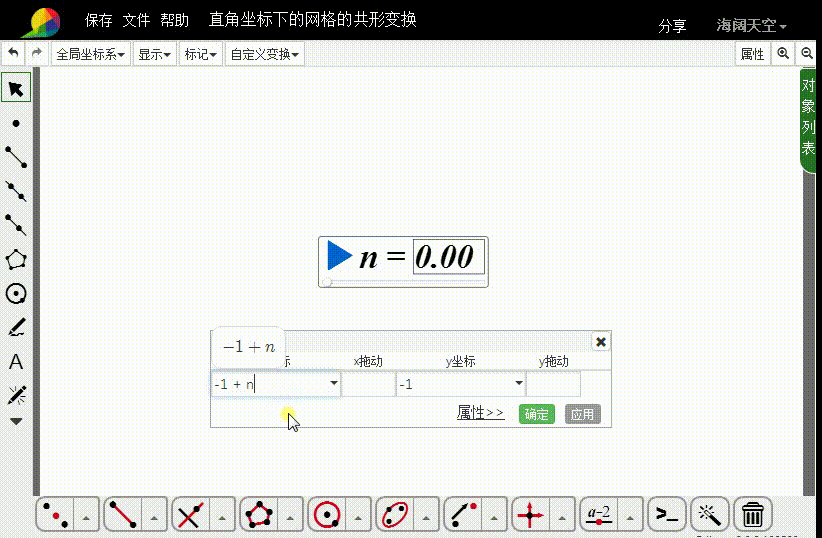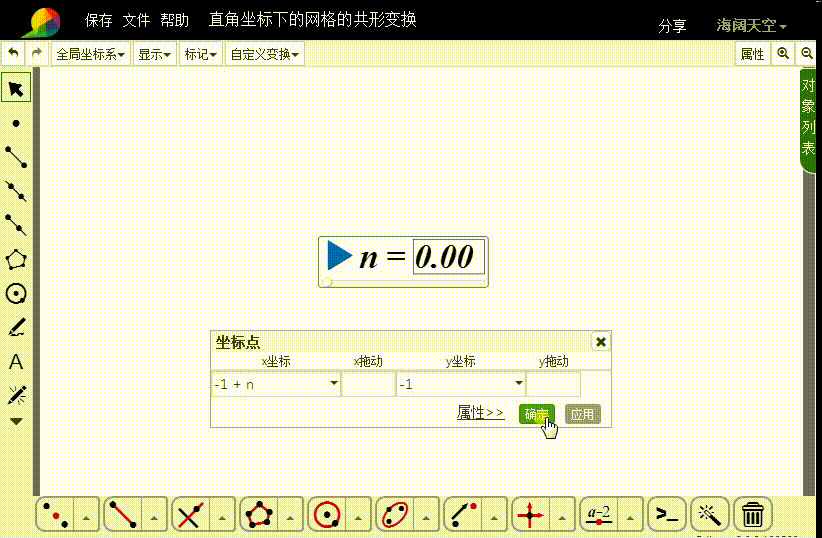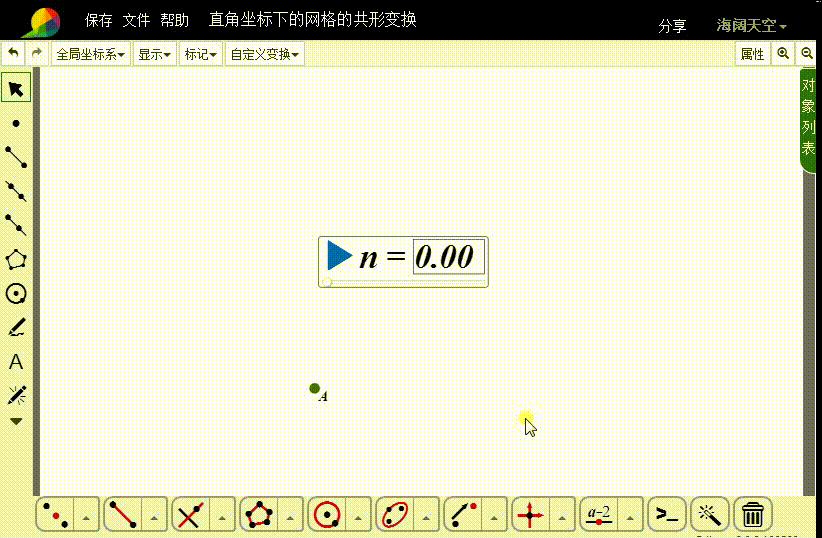
3、把A向上平移2个单位,得到点B;
连接线段AB。
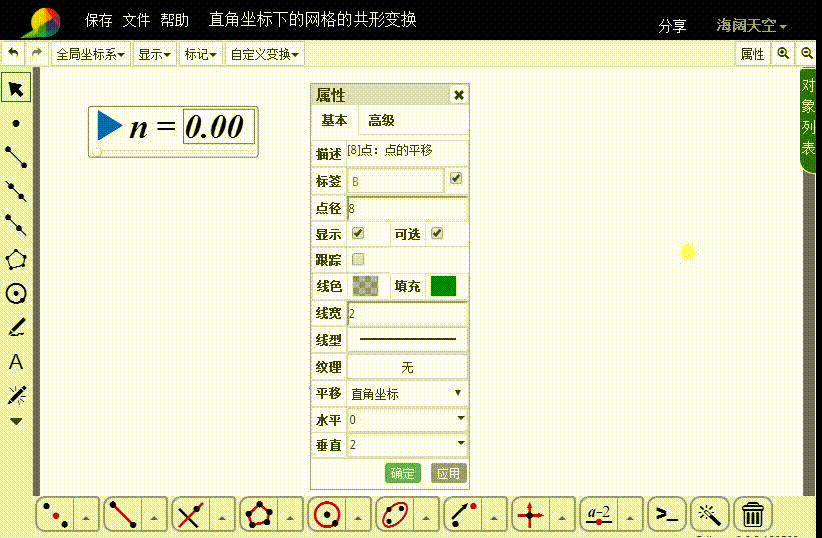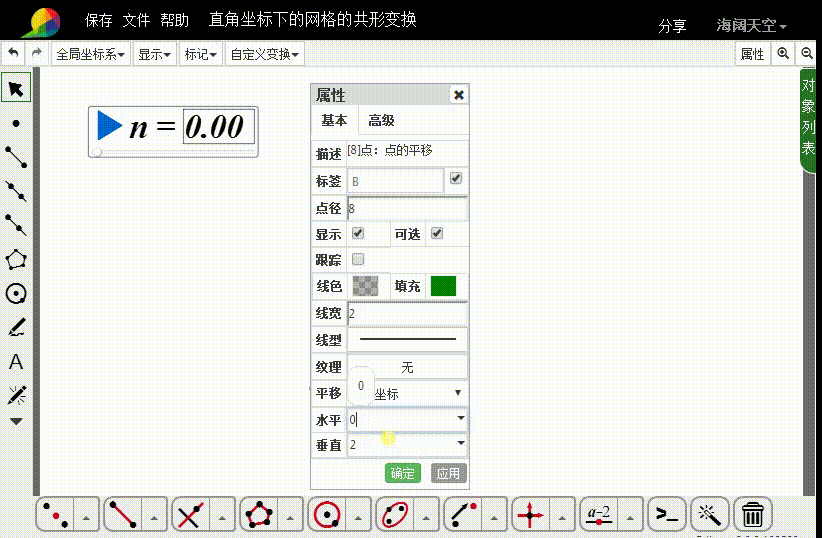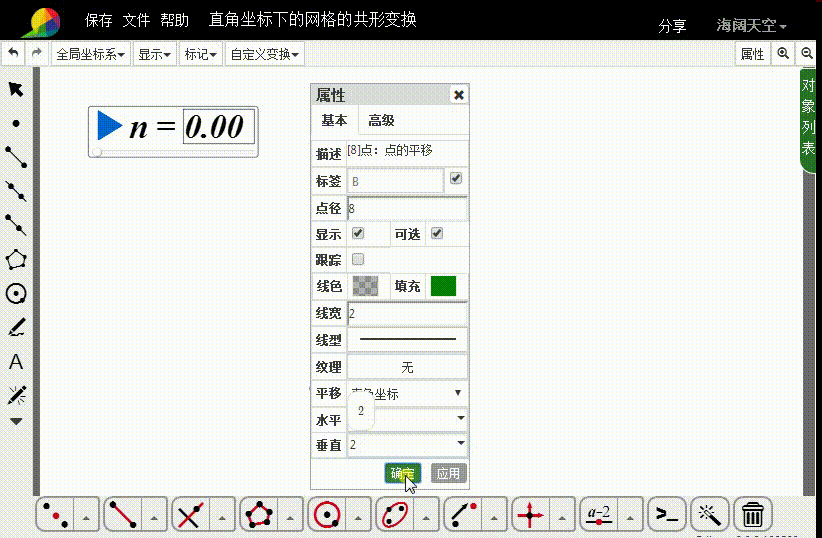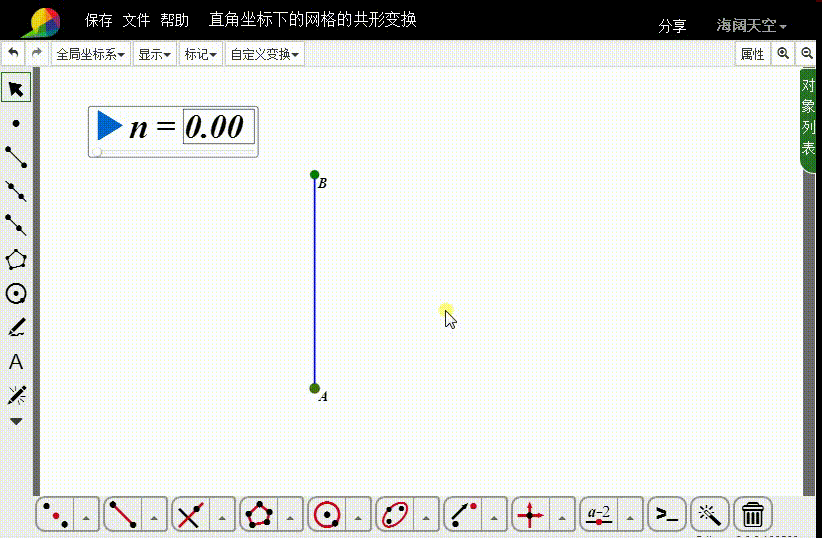
4、构造直角坐标点C,横坐标是-1,纵坐标是n-1;
C向右平移2个单位,得到D;
连接线段CD。

5、计算:
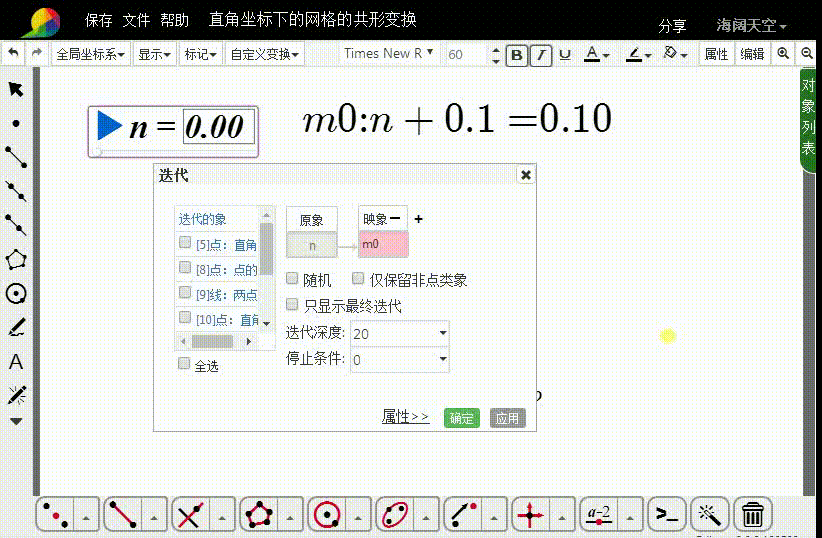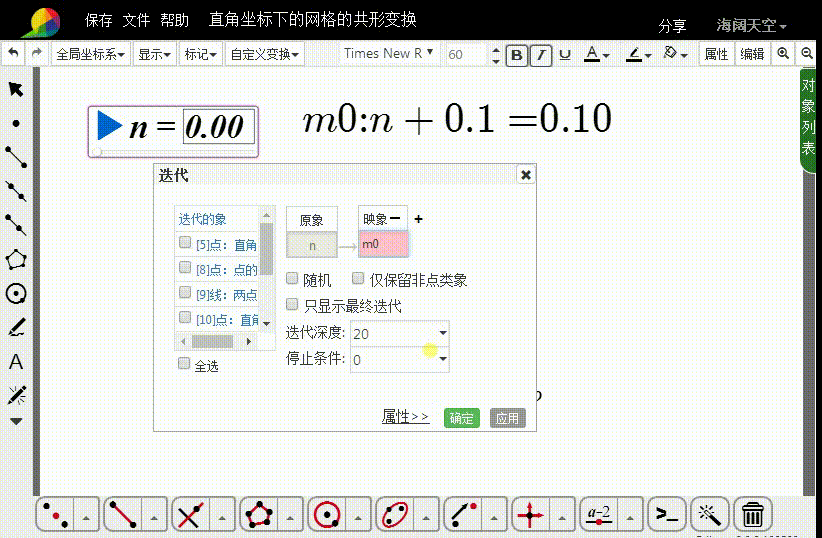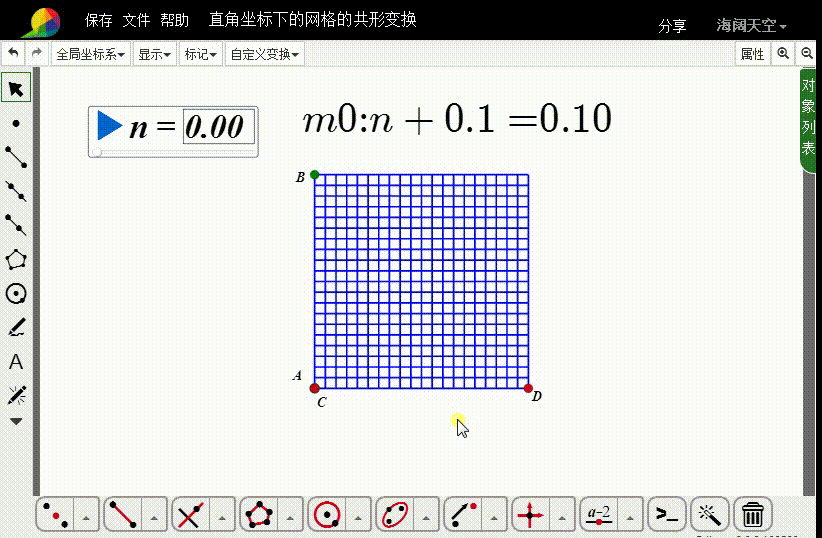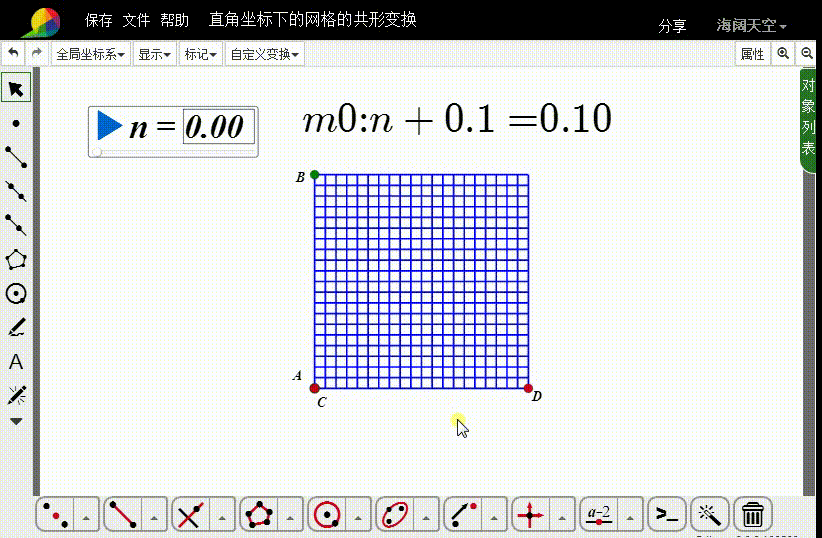
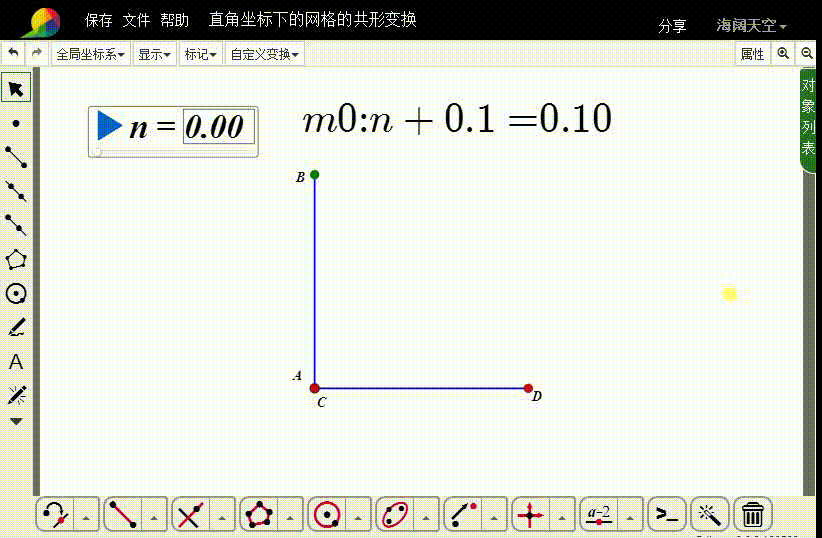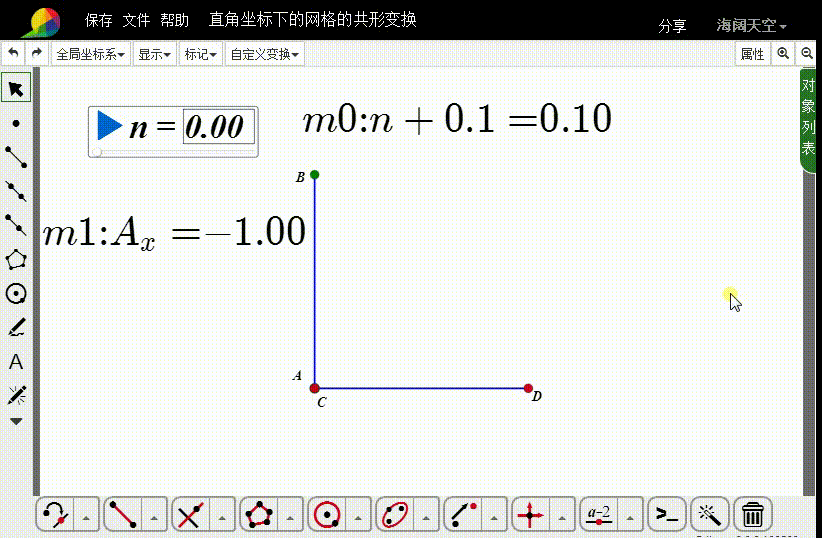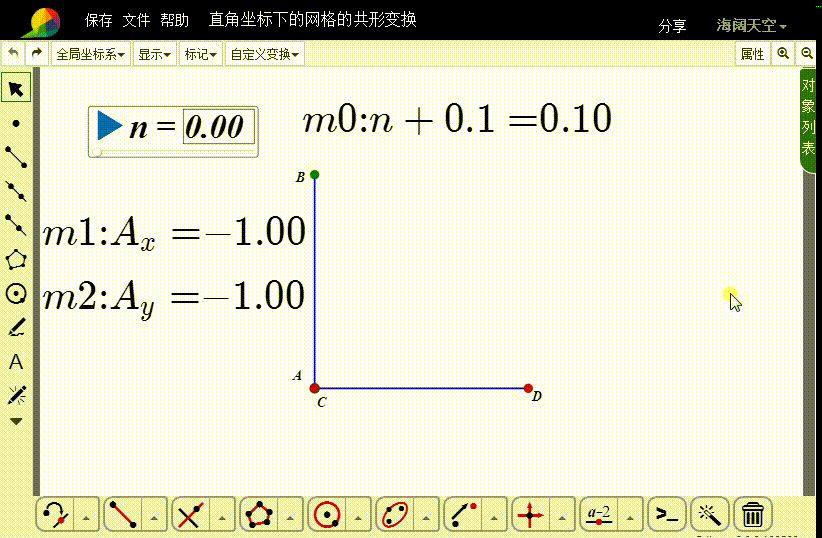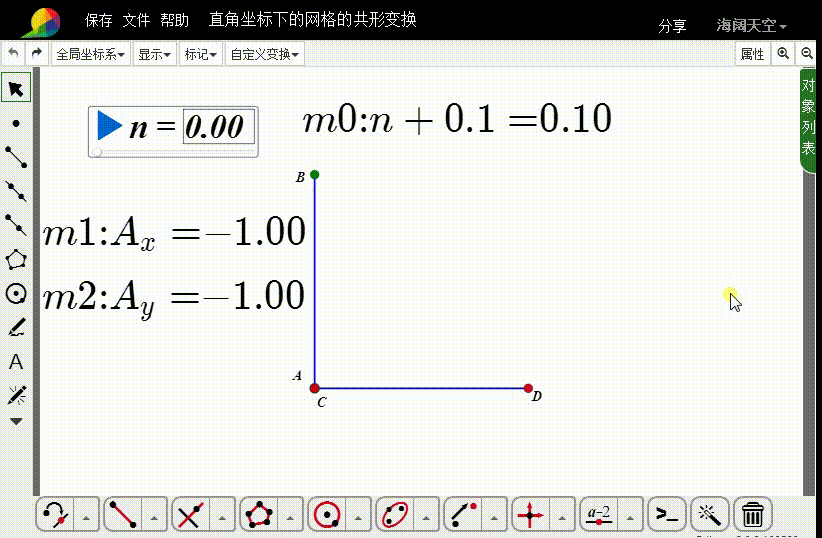
m0=n+0.1
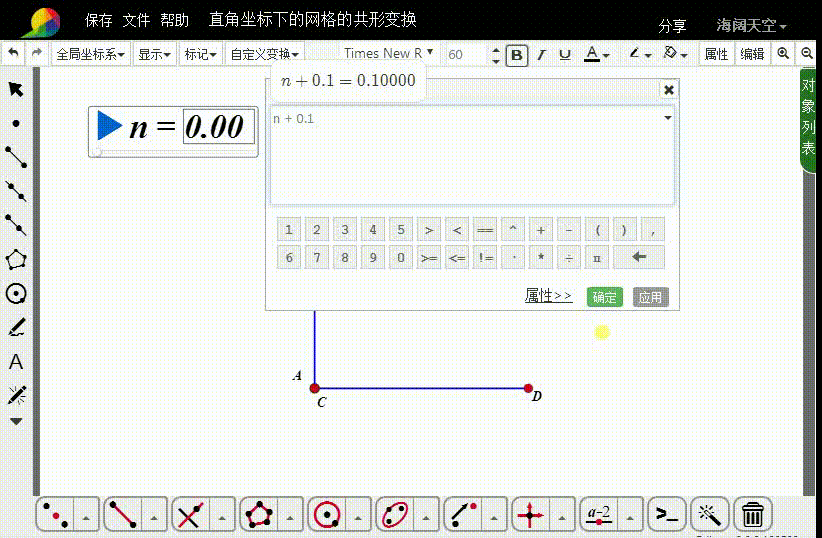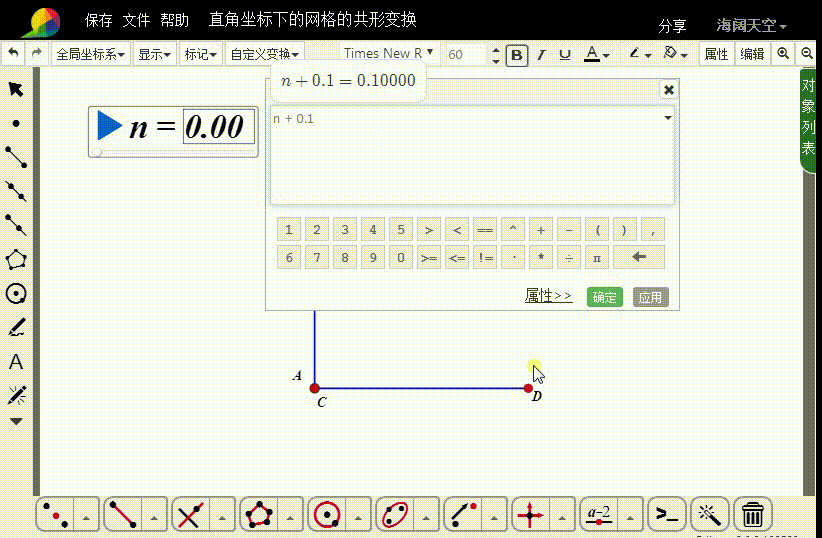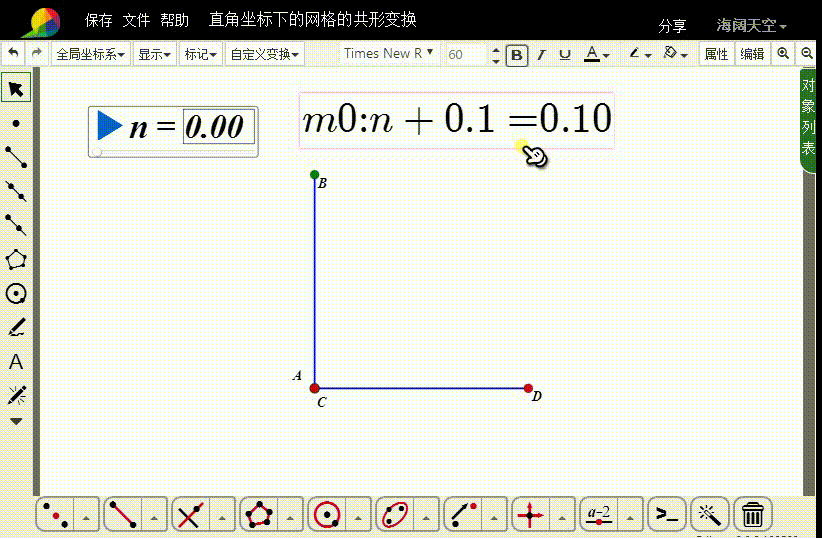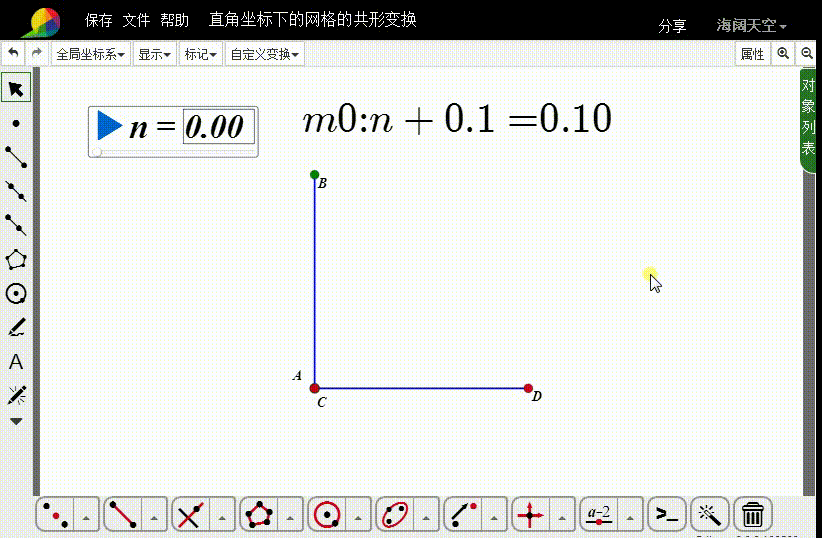
6、进行n→m0的变换,迭代深度是20。
迭代图像就是一个网格线。
1、测量A的坐标:
横坐标是m1,纵坐标是m2。
2、构造变量t。
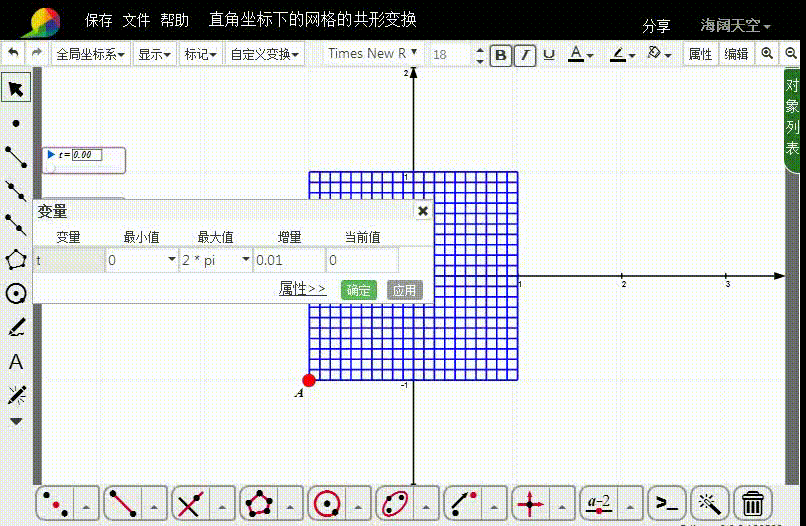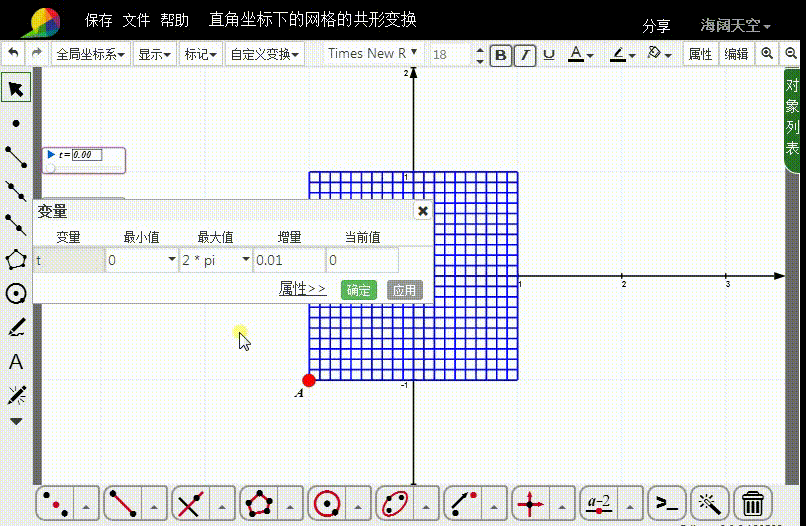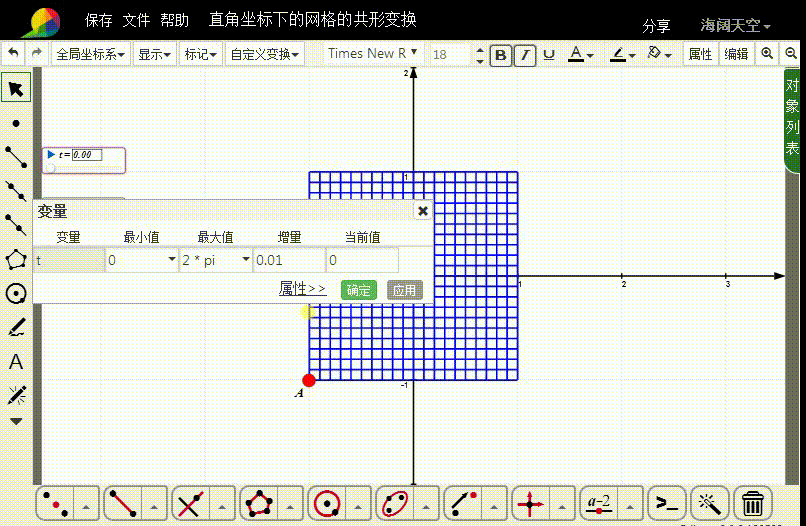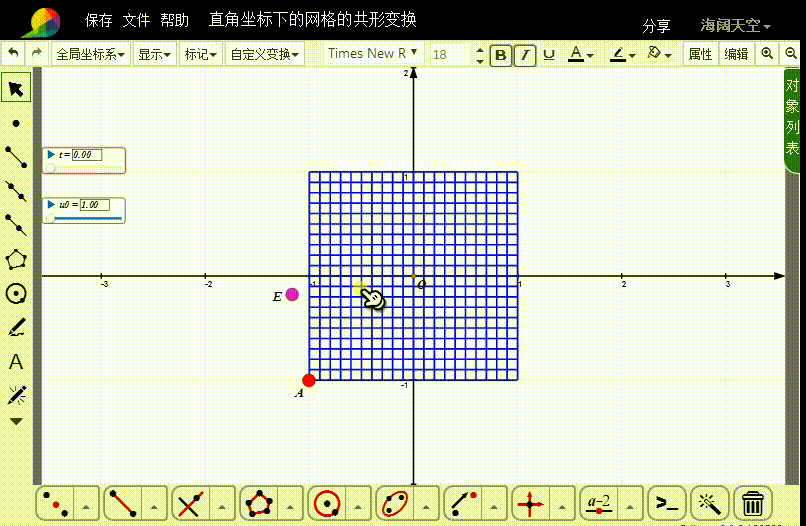
3、根据m1和m2,构造直角坐标点E:
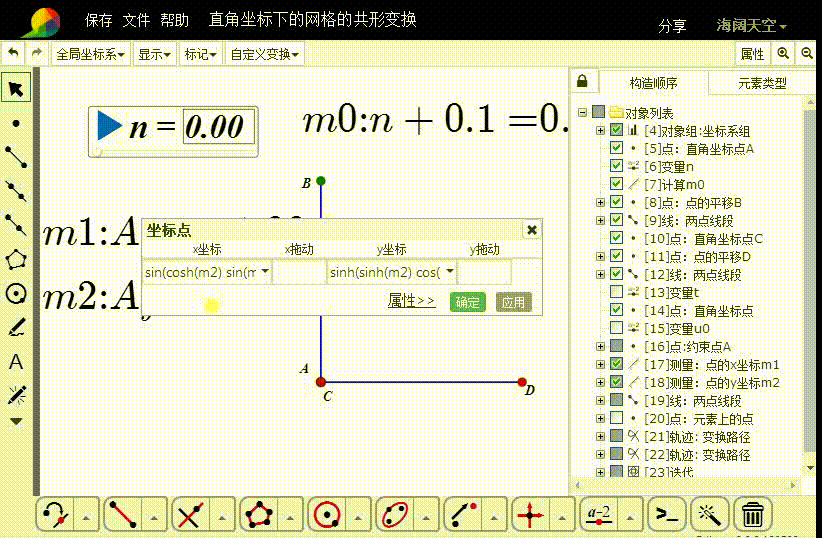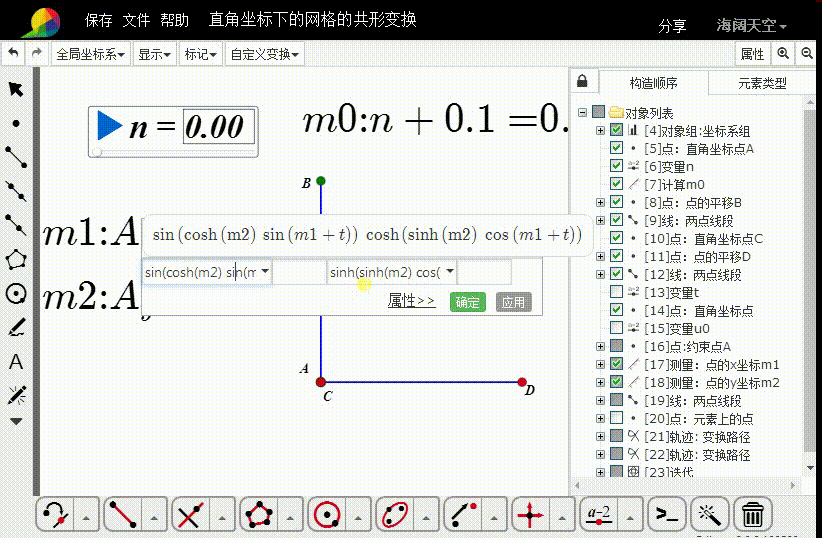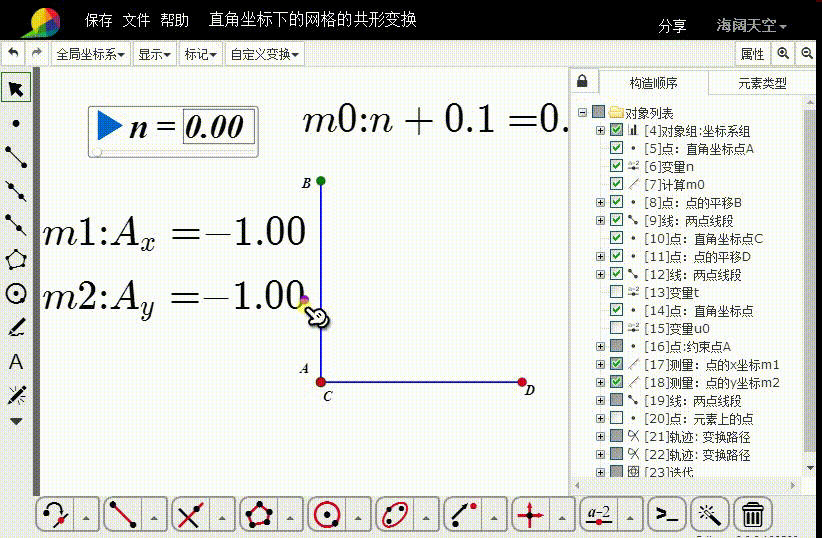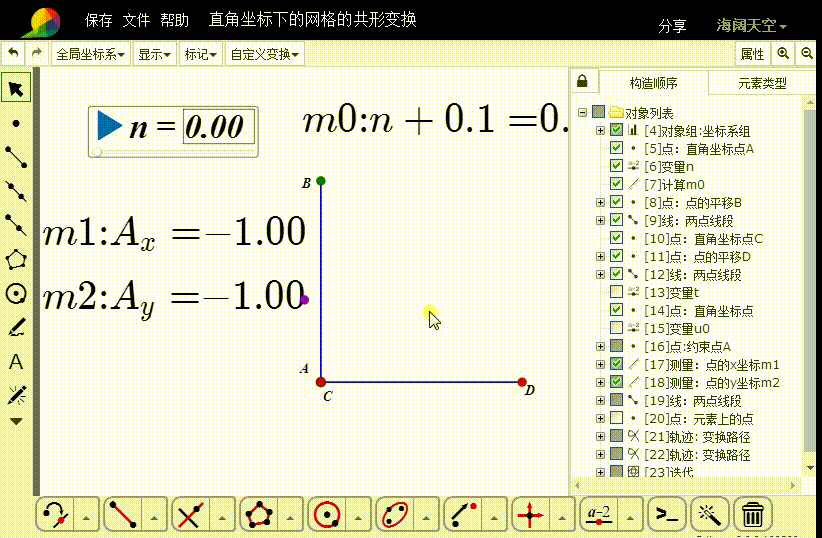
横坐标是 sin(cosh(m2) sin(m1 + t)) cosh(sinh(m2) cos(m1 + t))
纵坐标是 sinh(sinh(m2) cos(m1 + t)) cos(cosh(m2) sin(m1 + t))
这相当于是把 z=m1+m2*I 变成 sin(sin(z))
4、连接线段AE,在AE上取动点F。
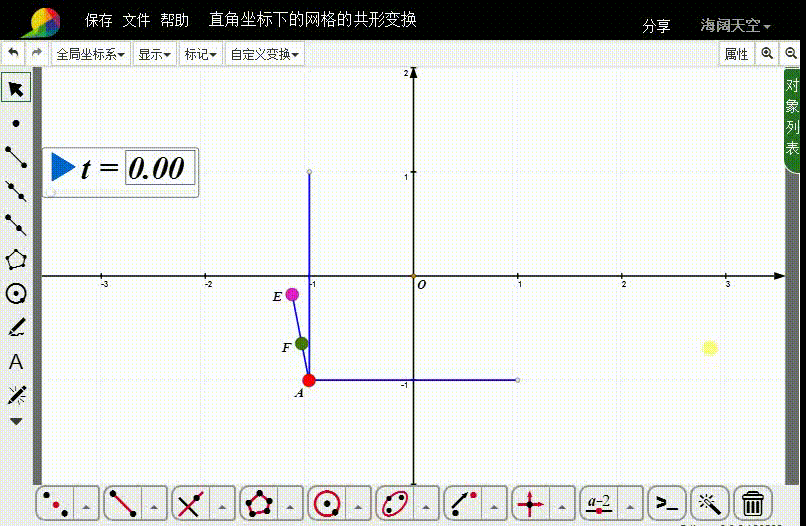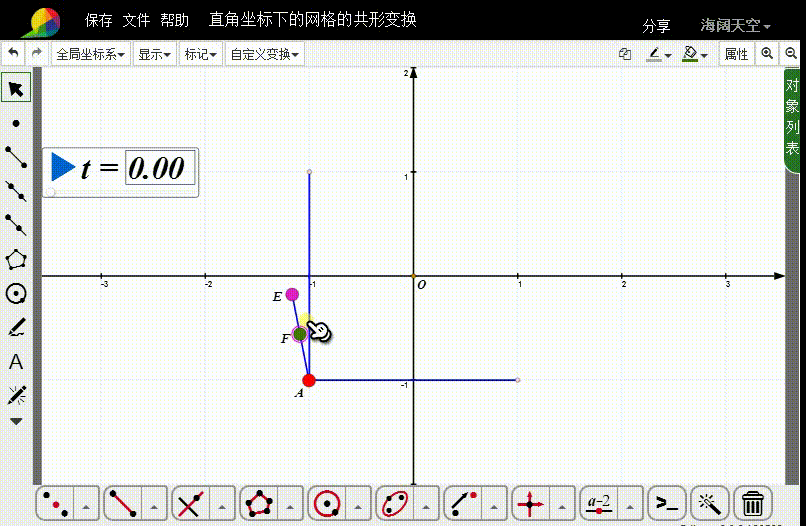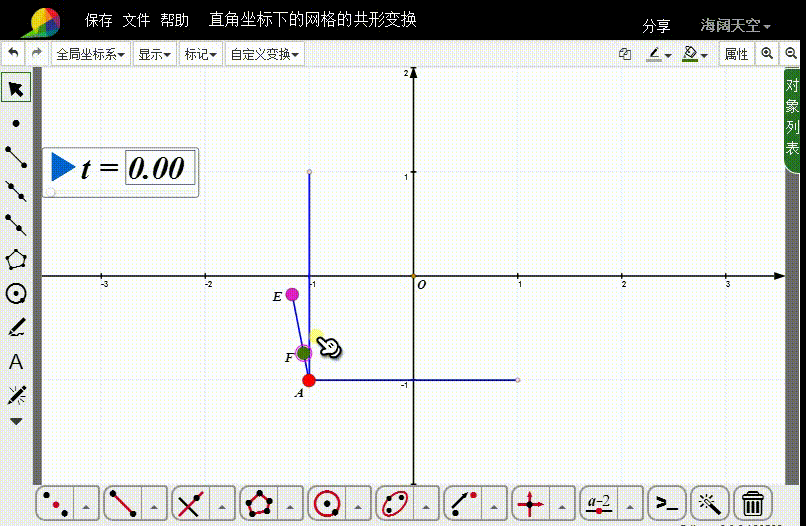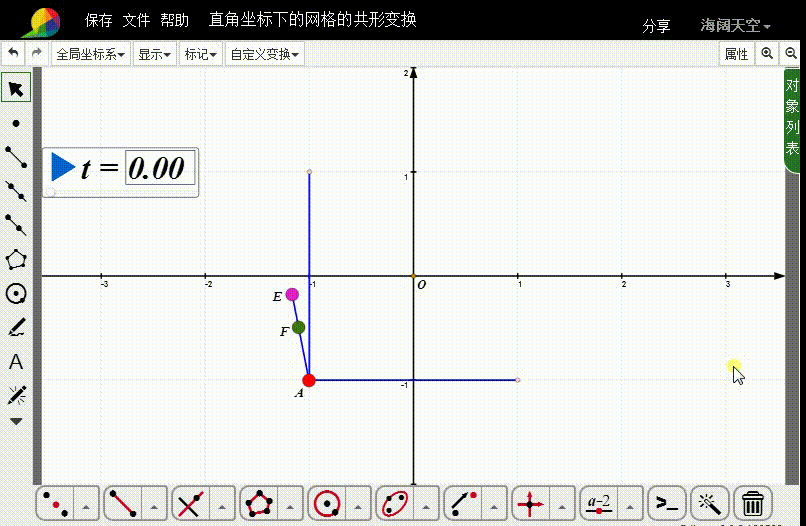
5、选择A和F,构造自定义变换。
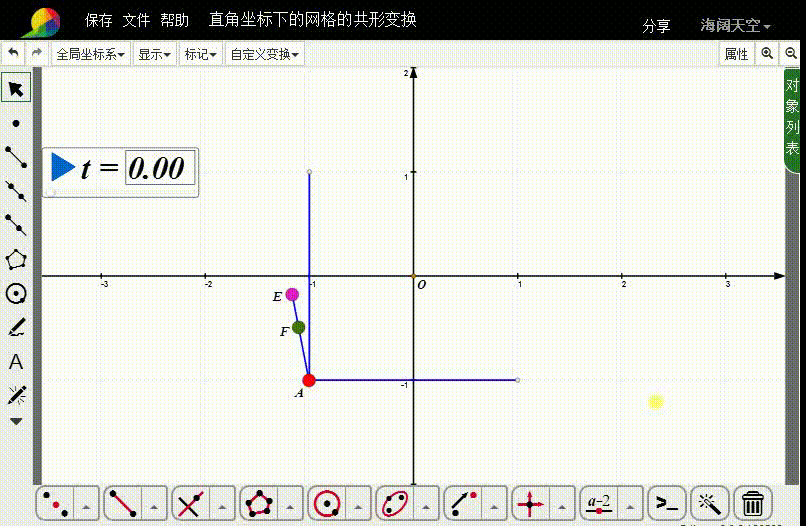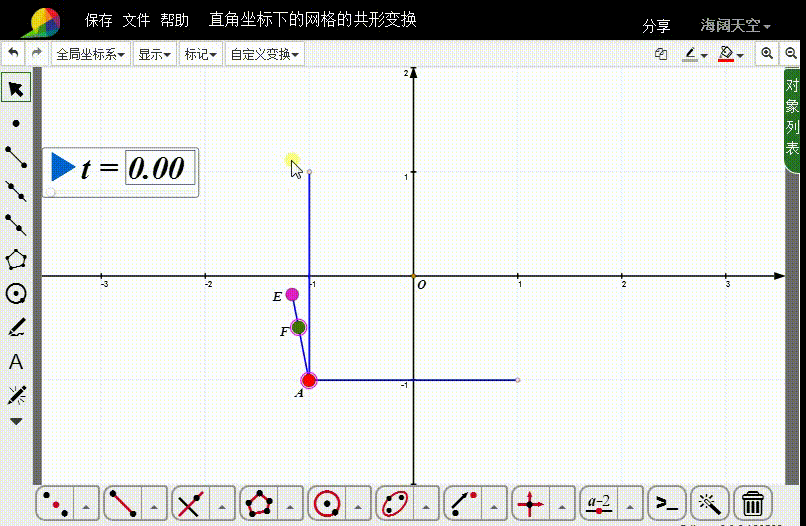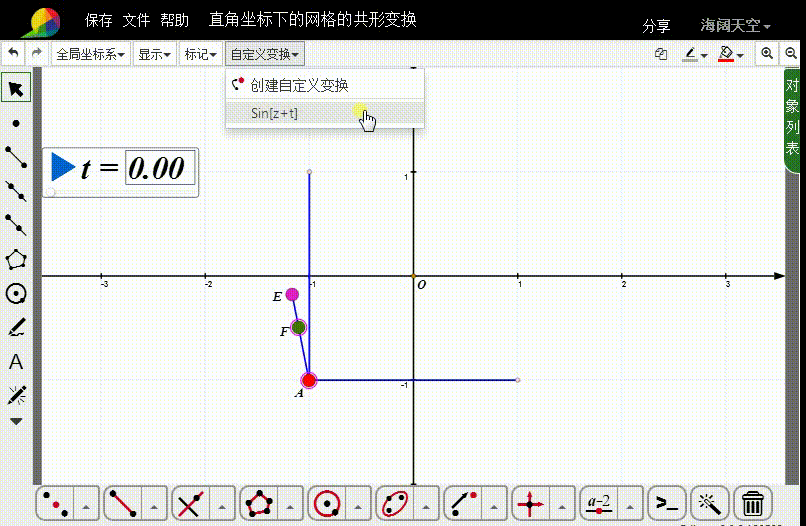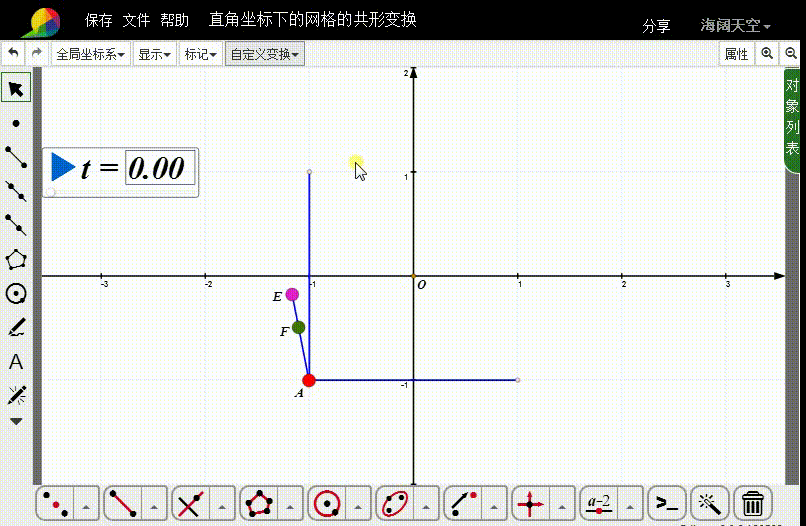
6、对线段AB和CD进行自定义变换。
把两个变换曲线的样本数都改为36。
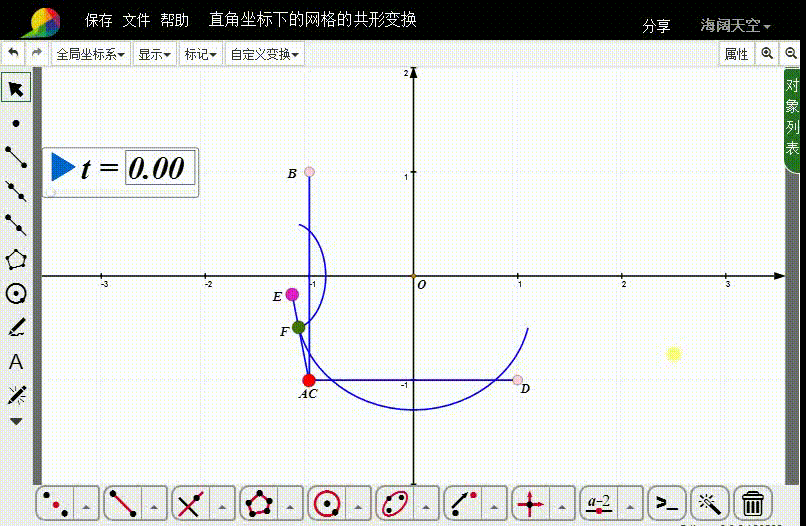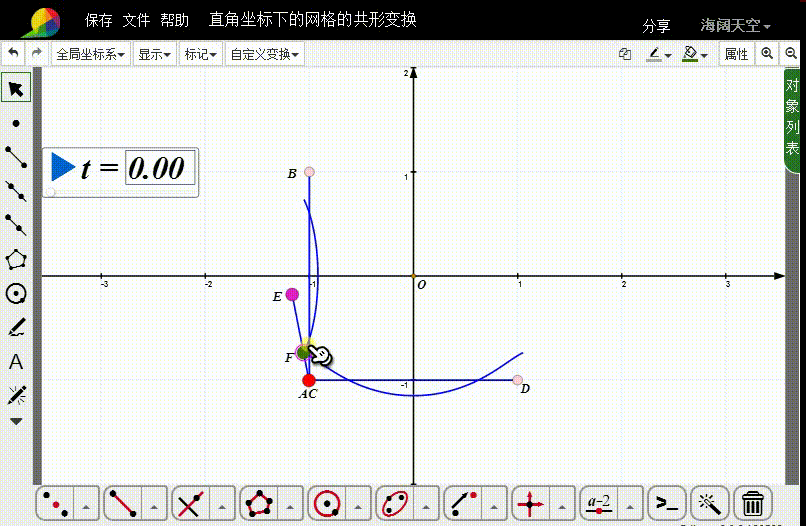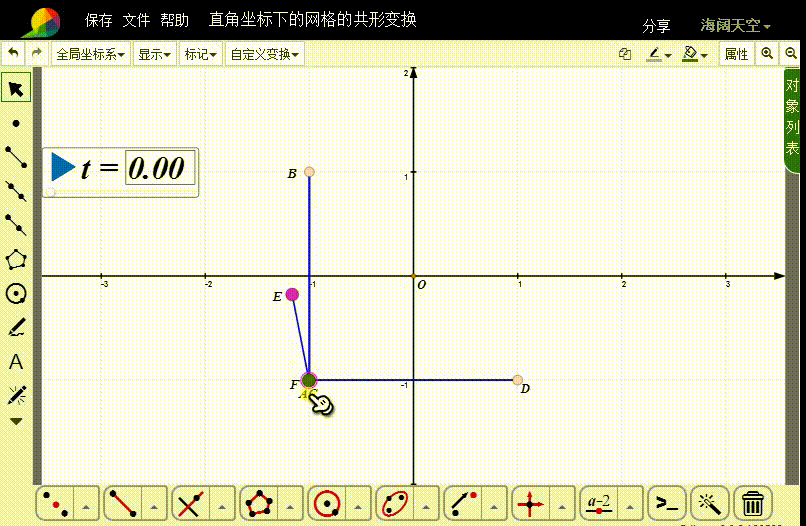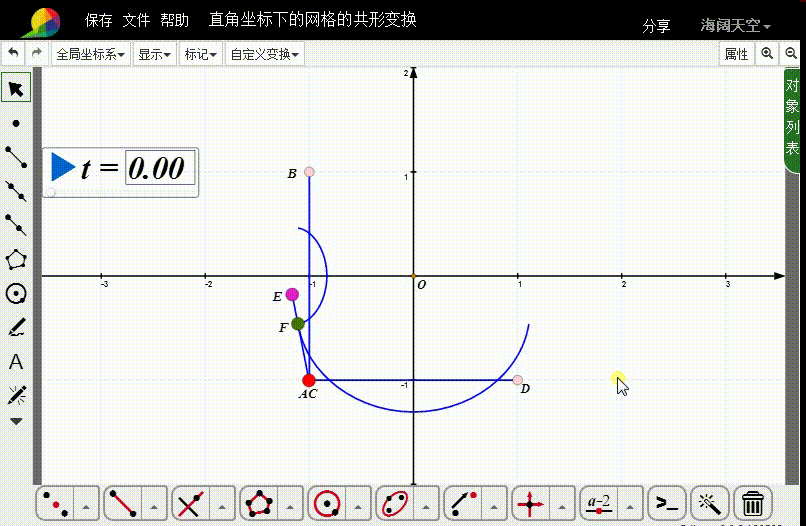
7、删除上一部分的迭代;
隐藏线段AB和CD;
进行新的迭代,n→m0。

8、那么,F点就控制着图像变换的具体动画。
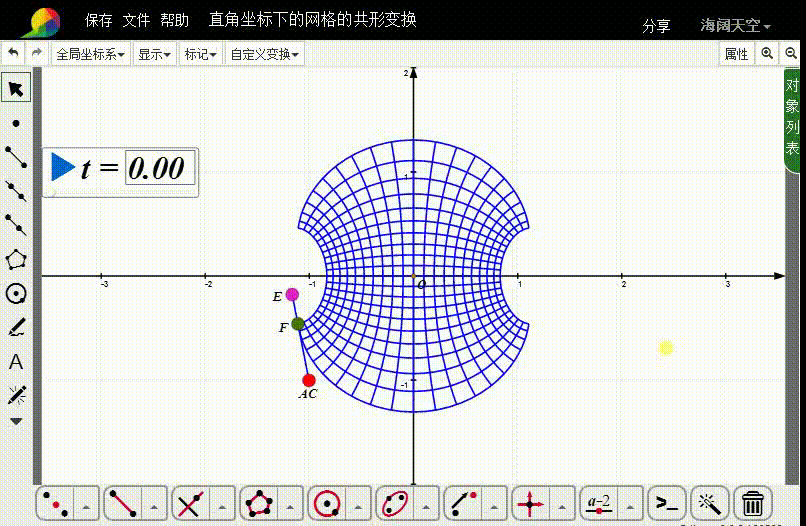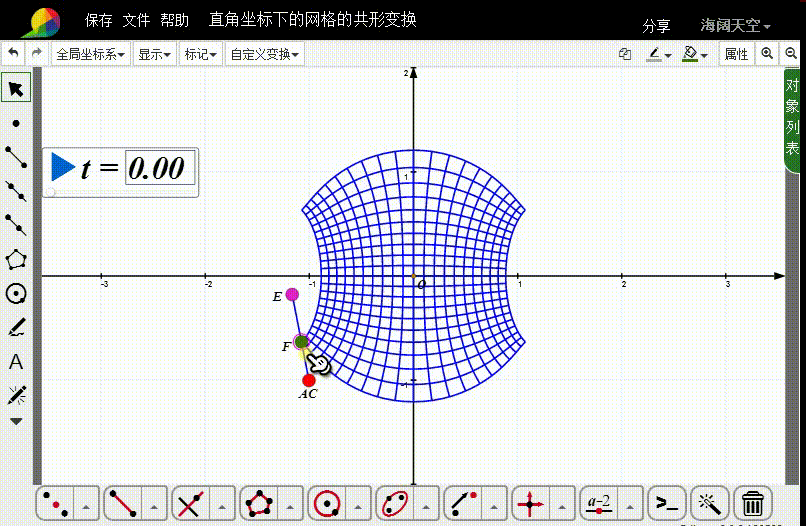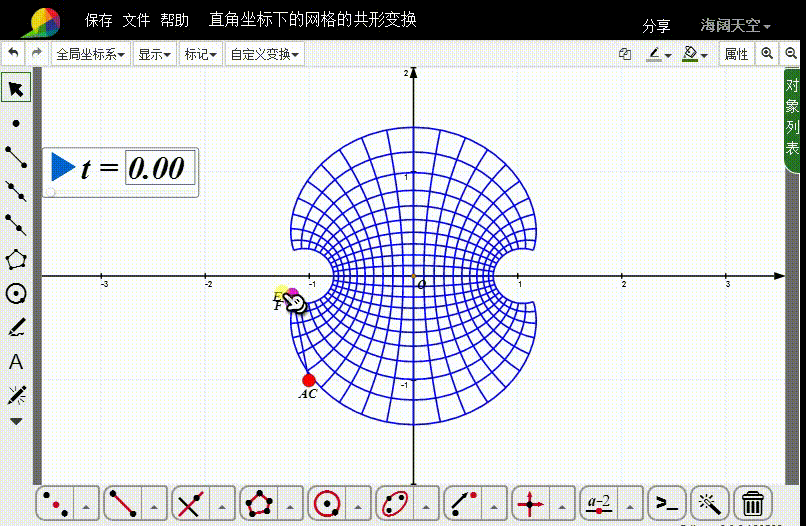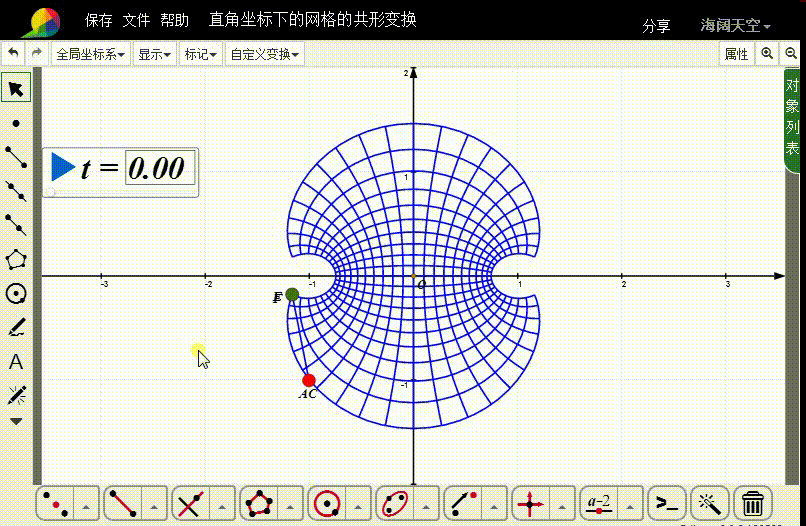
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:70
阅读量:166
阅读量:36
阅读量:47
阅读量:122