线性变换与矩阵乘法的联系

1、假设X代表五维空间里面的点坐标：

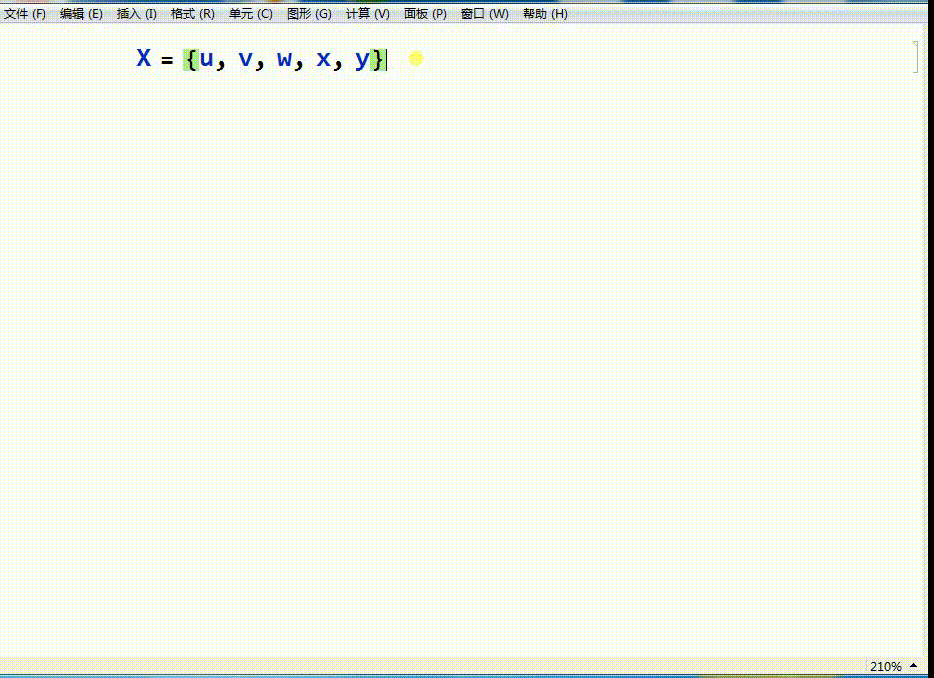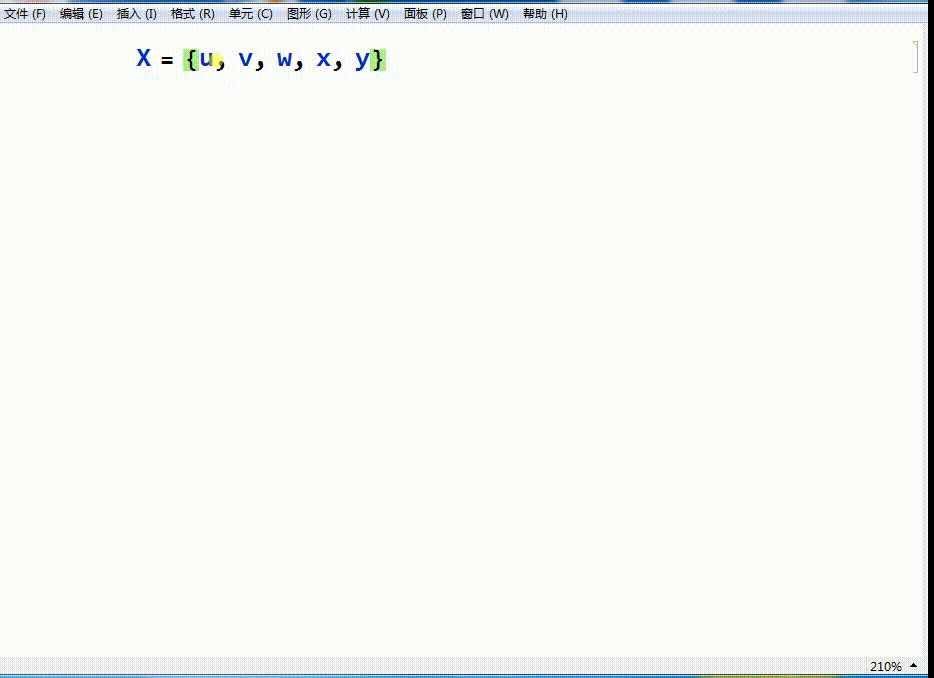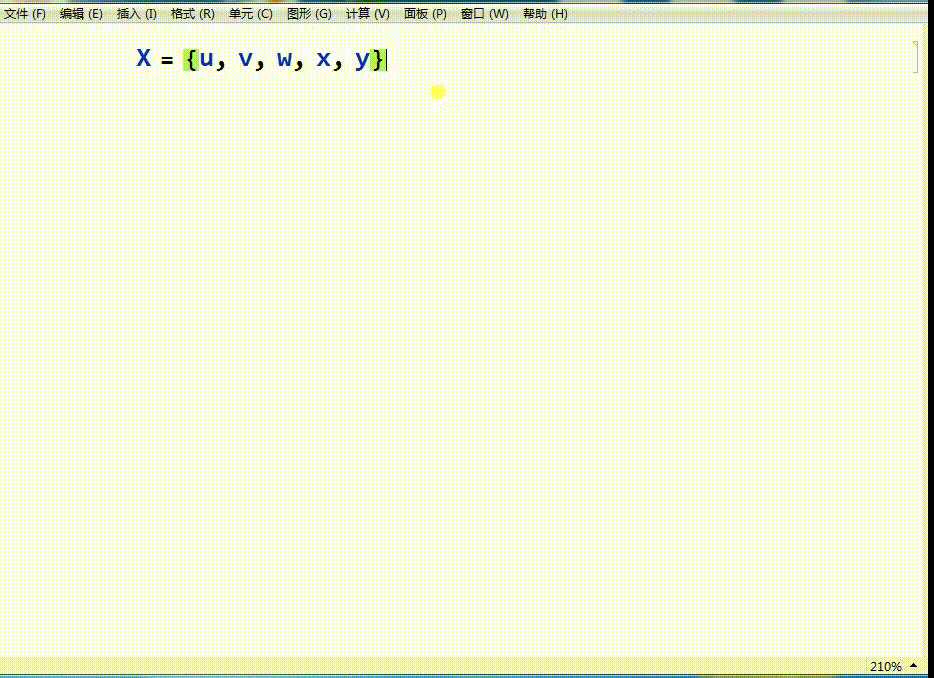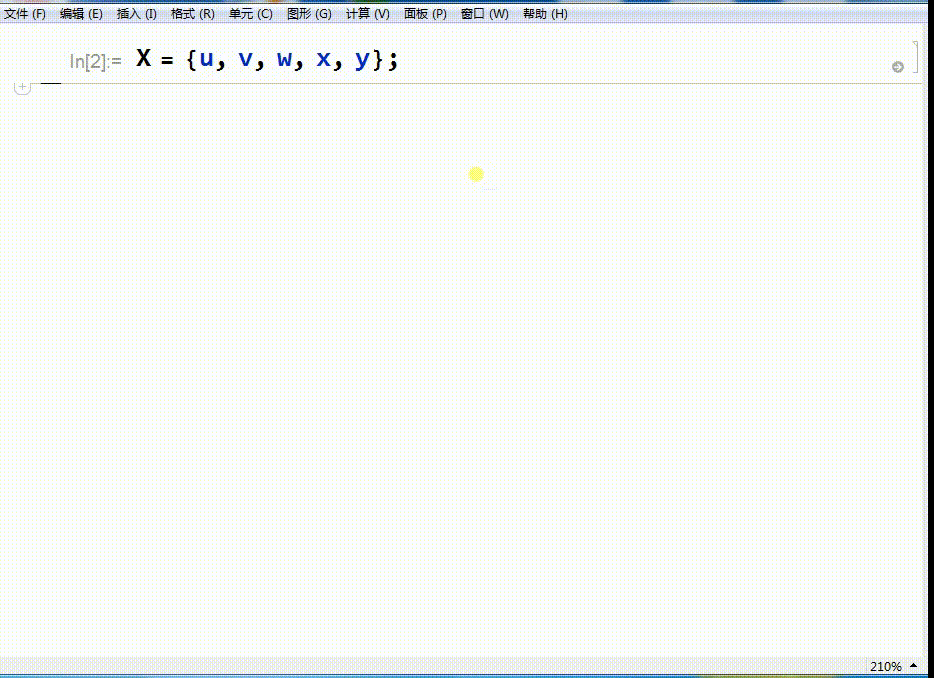
X={u,v,w,x,y}

其中，u,v,w,x,y是五个数字。

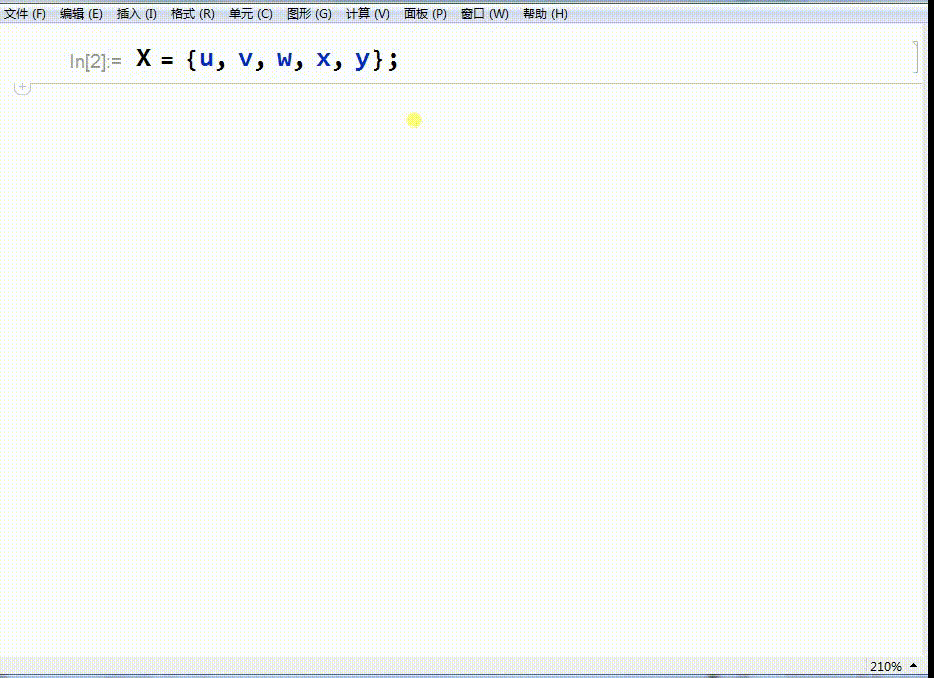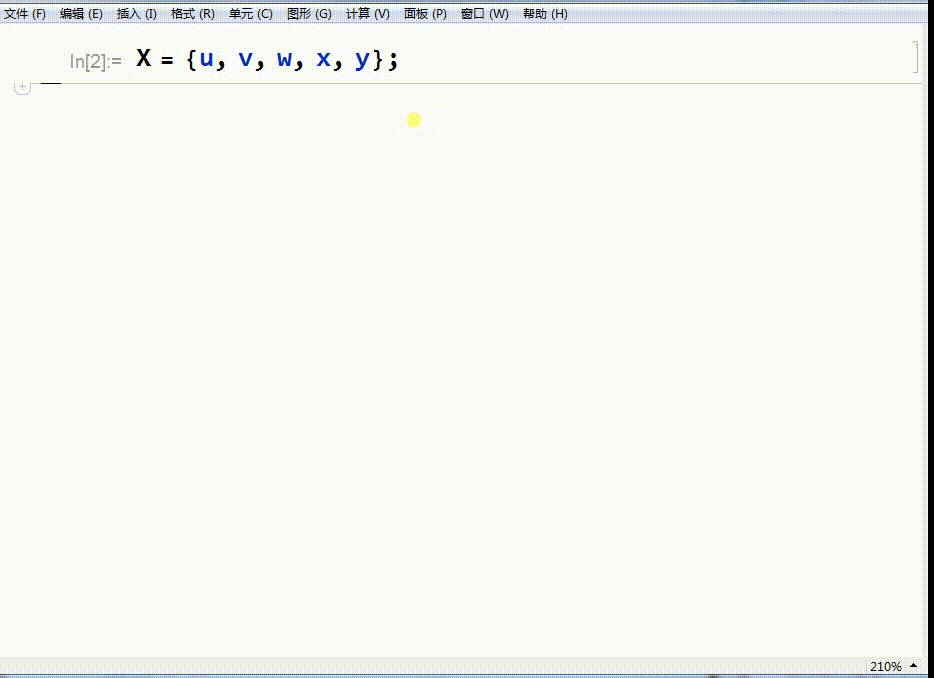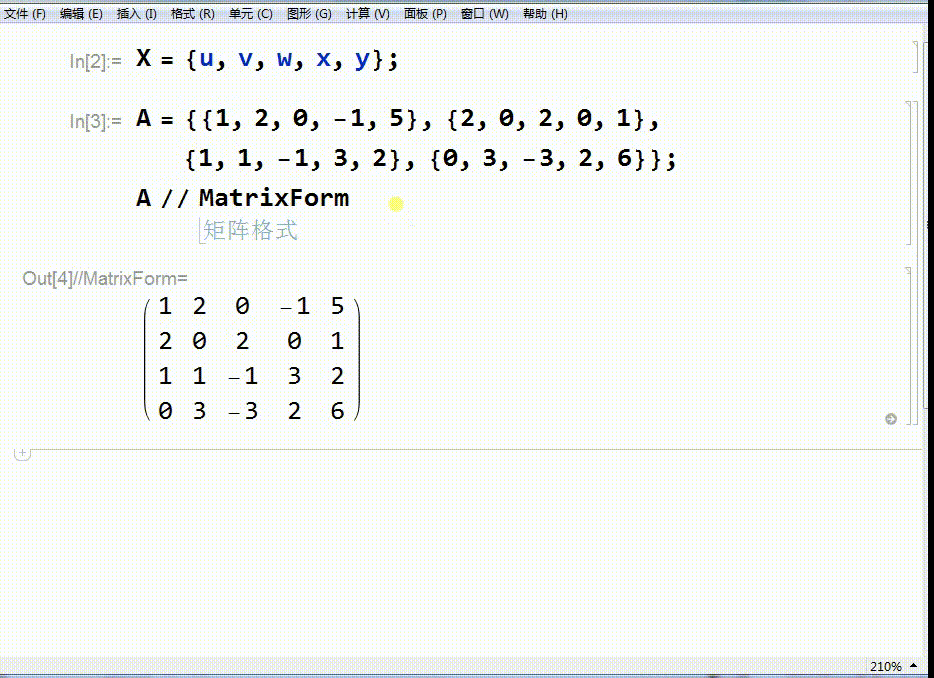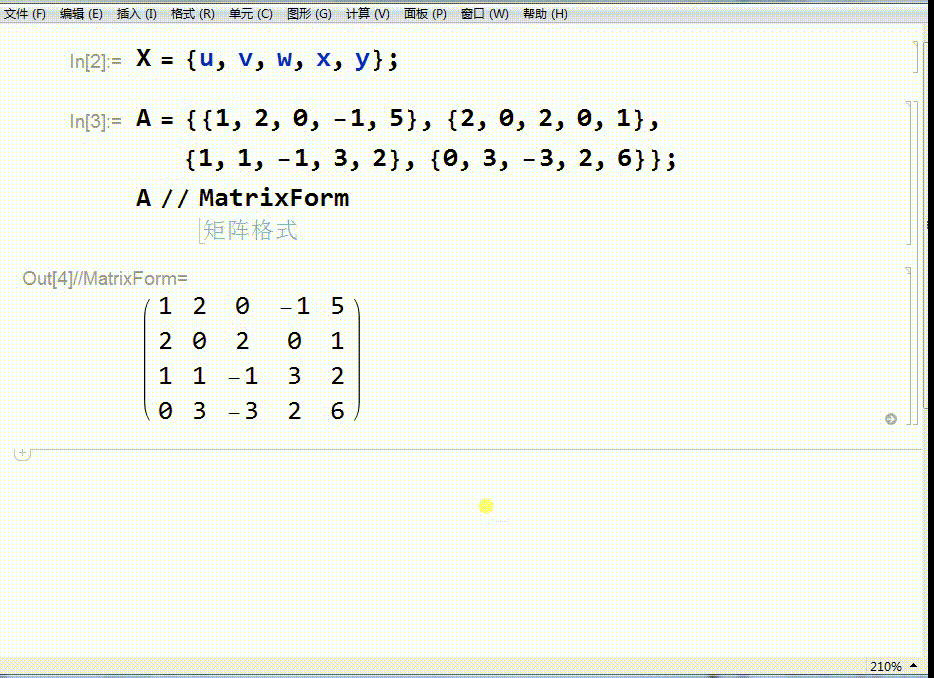
2、给定矩阵A：

A = {{1, 2, 0, -1, 5}, {2, 0, 2, 0, 1}, {1, 1, -1, 3, 2}, {0, 3, -3,  2, 6}}

3、A左乘X，得到新的坐标点X1。

X1是四元数组，相当于四维空间里面的点坐标。

A.X就相当于把五维空间里面的点，转化为四维空间里面的点。

4、给出五维空间里面若干点：

Y = {a, b, c, d, e};

Z = {p, q, r, s, z};

U = {a, c, p, q, u};

V = {x, y, u, b, d};

T = {e, f, g, h, i};

这些点的集合，记为B：

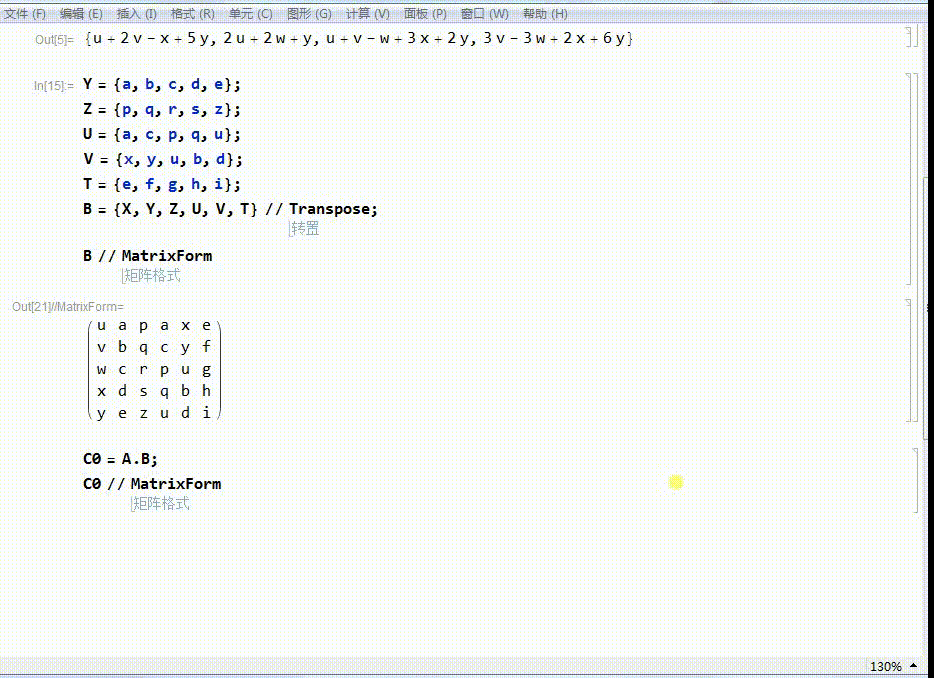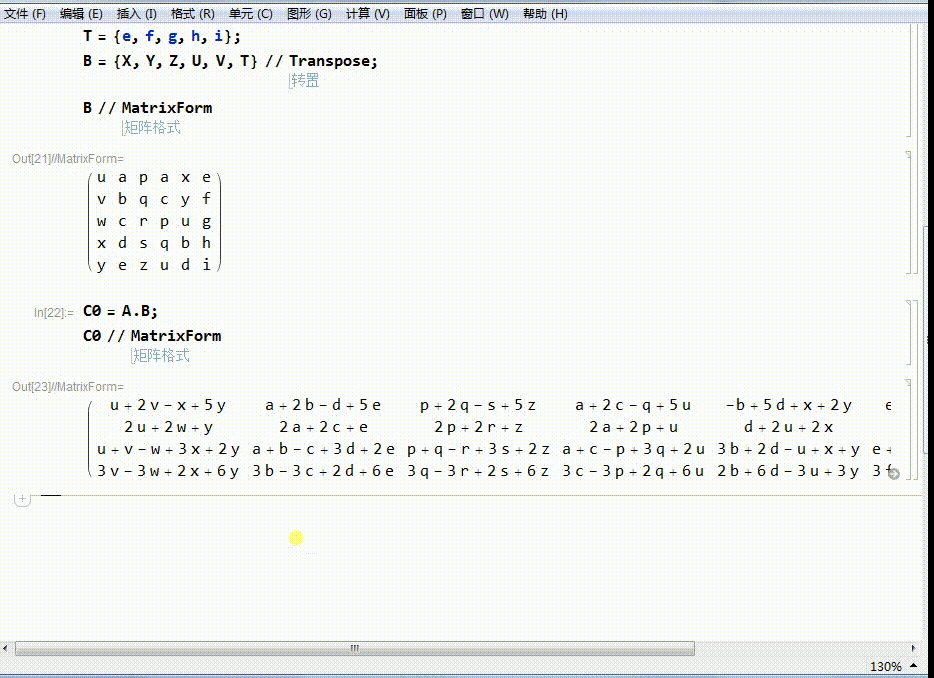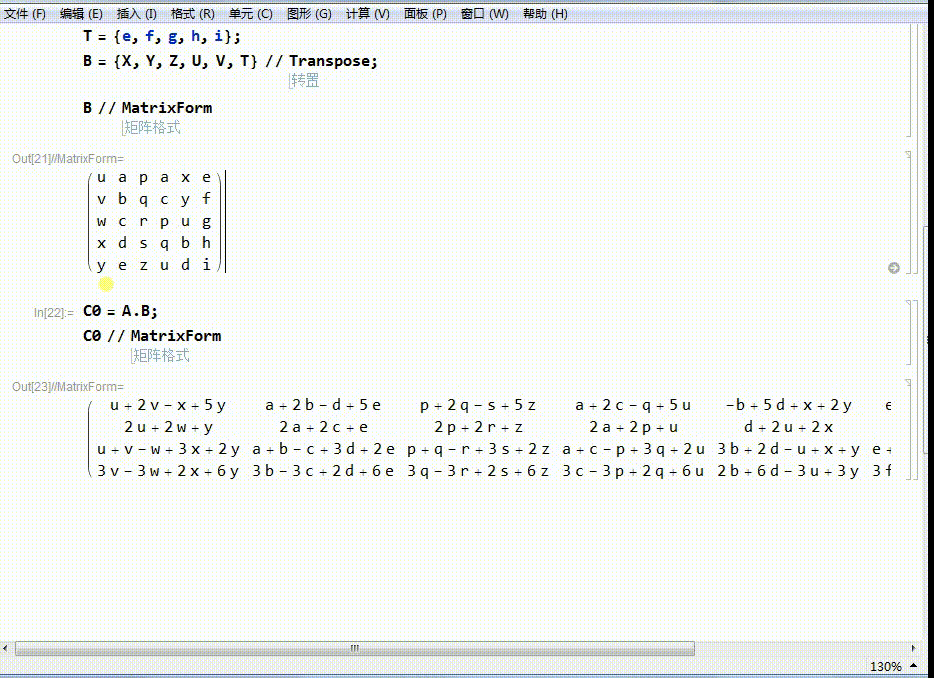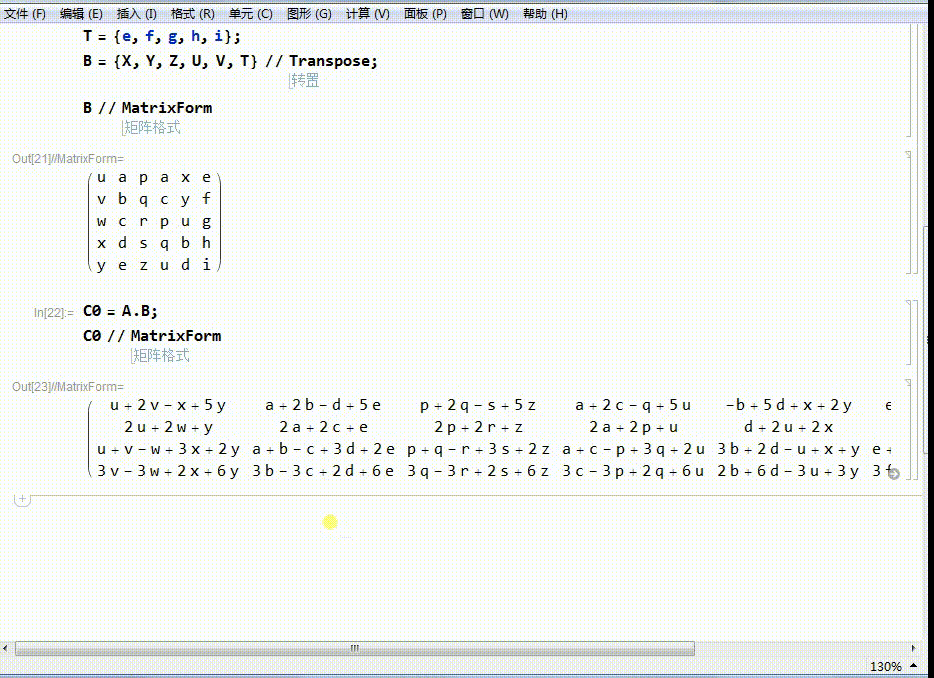
B = {X, Y, Z, U, V};

那么，B转置一下就相当于一个行数为5的矩阵。

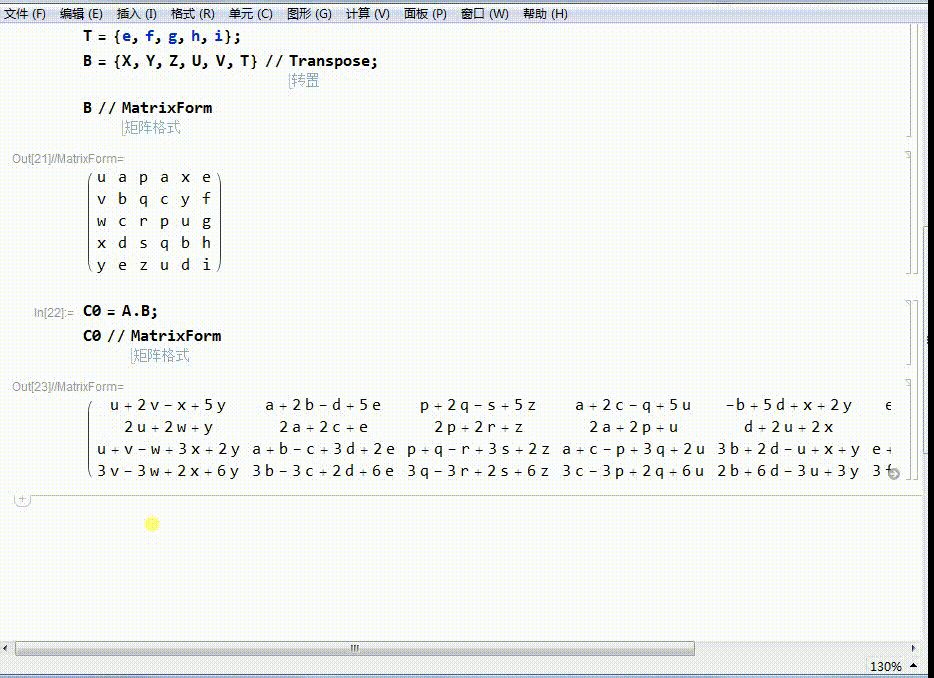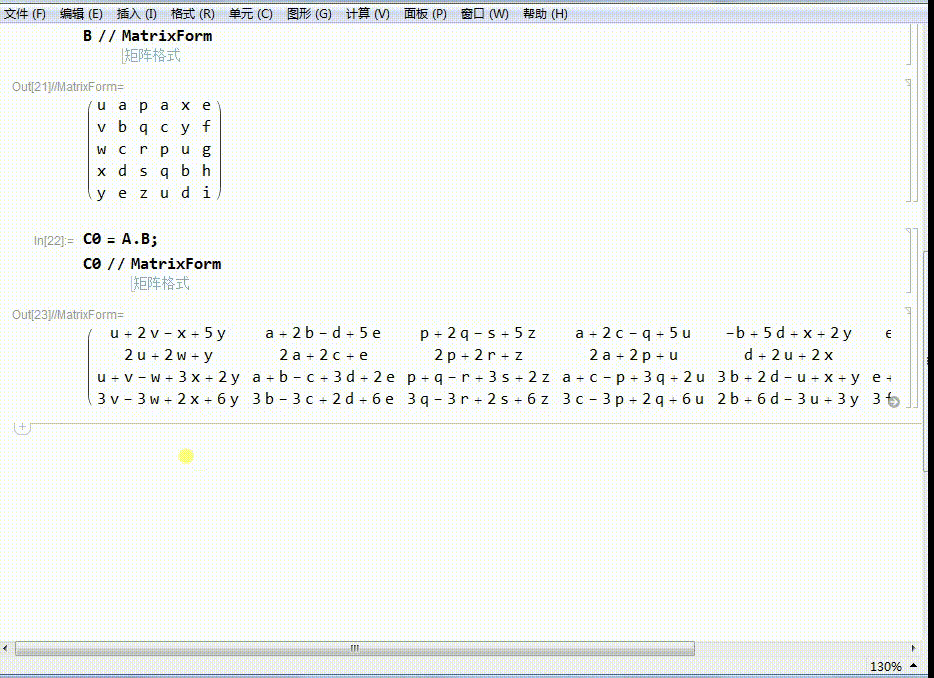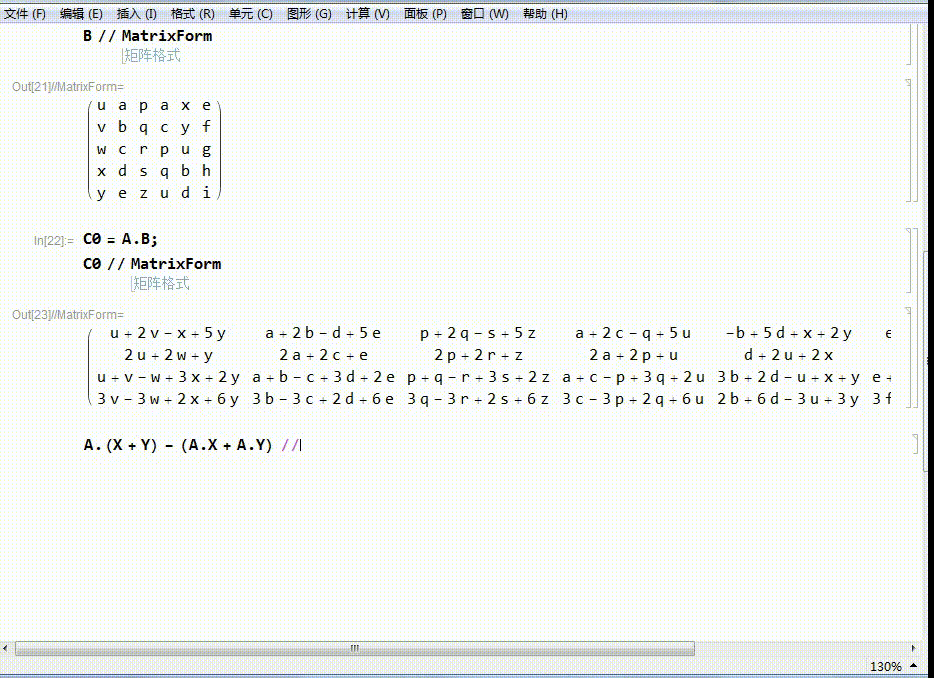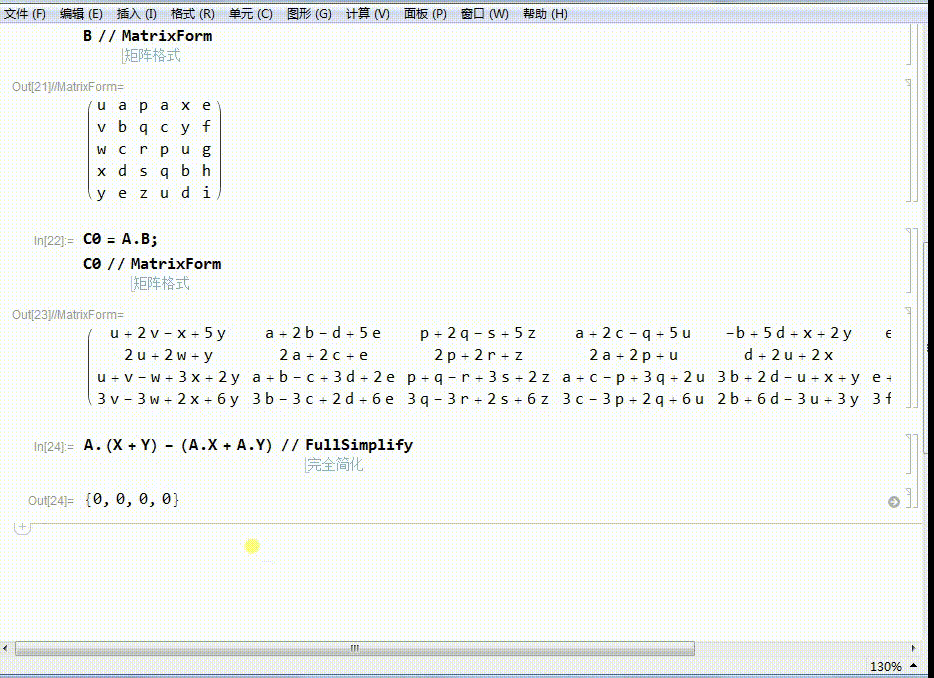
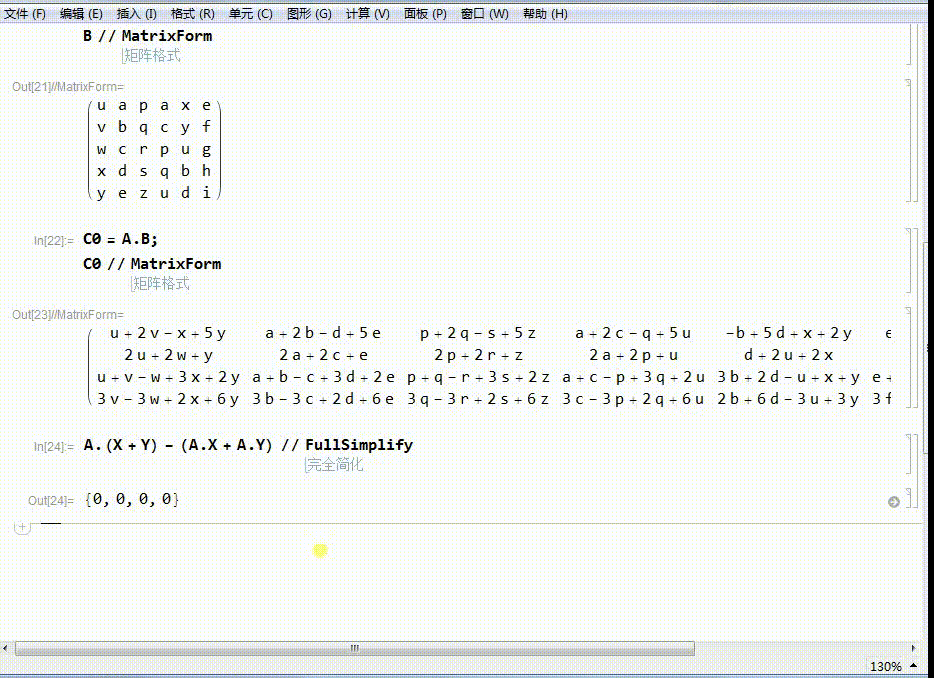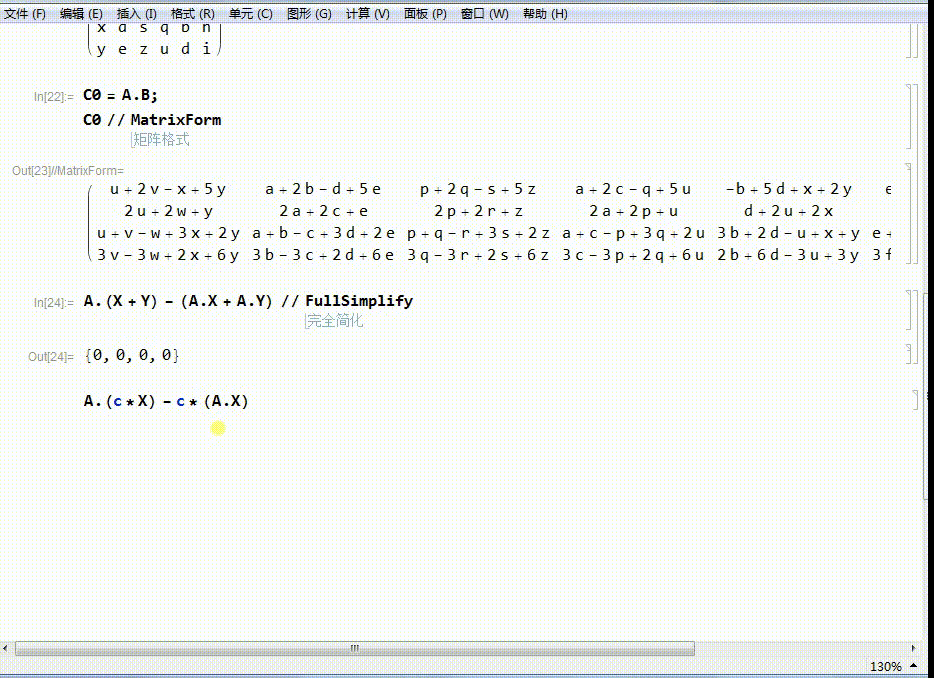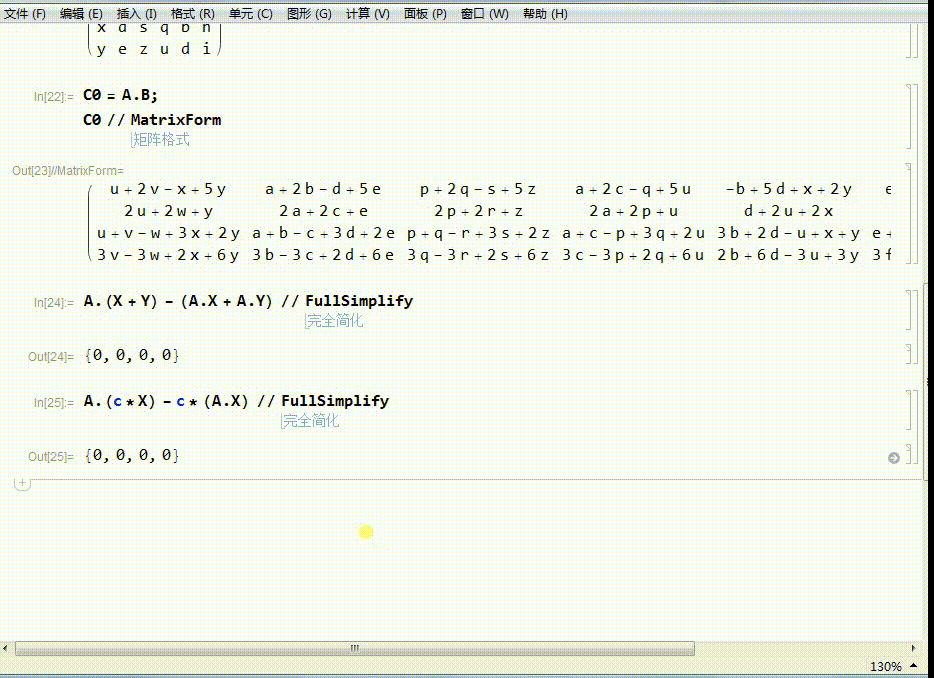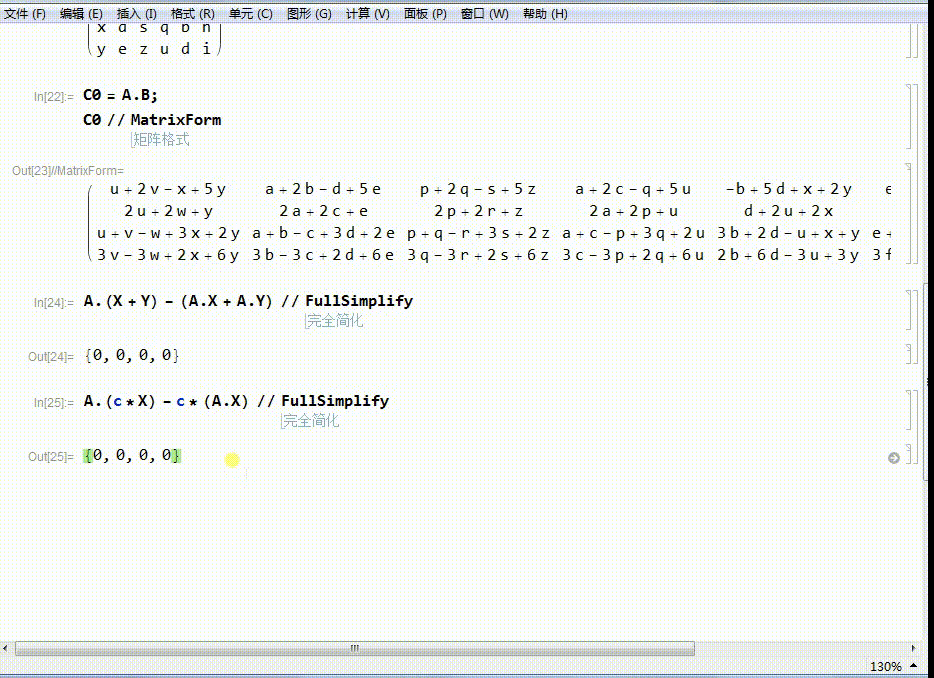
5、A左乘B，得到一个新的矩阵C0.

C0的行数为4，相当于把B里面的每一个点（列向量），变成了C0里面的新的点（列向量）。

6、要证明这是线性变换，需要证明两个结论，其中一个是：

A.(X+Y)-(A.X+A.Y)=0

7、另一个结论是：

A.(c*X)-c*(A.X)=0

注意，上面的0指的是0向量。