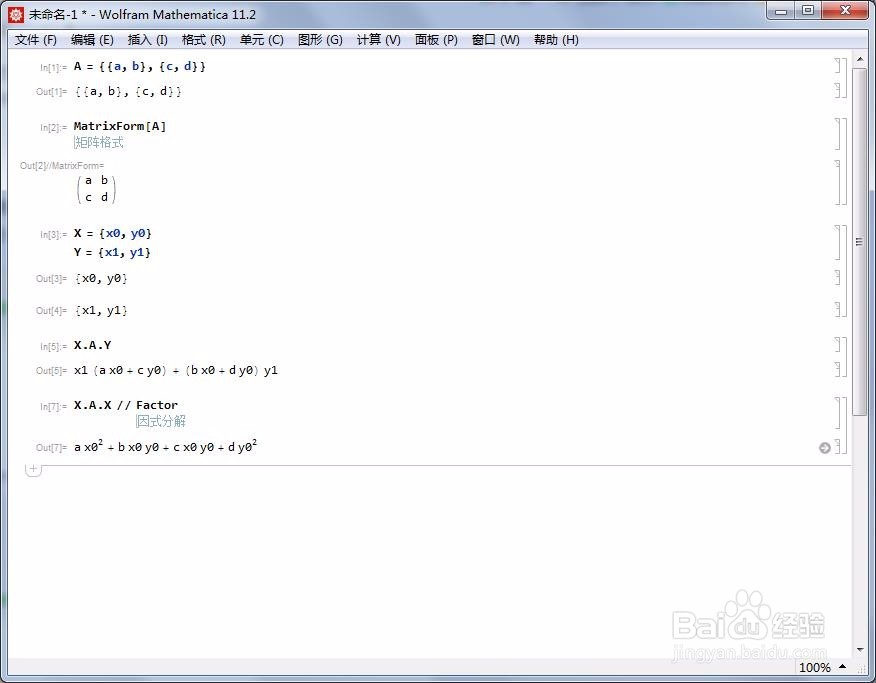
2*2的正定矩阵的判定

1、正定矩阵是从双线性型引申出来的。

给定双线性型<X,Y>=X'AY，其中X'表示向量X的列向量形式。

如果：

X = {x0, y0}

Y = {x1, y1}

那么，X.A.Y在Mathematica就表示了上面的双线性型，结果等于：

x1 (a x0 + c y0) + (b x0 + d y0) y1

2、而如果A是正定矩阵，那么，对于非零向量X，<X,X>大于0。

X.A.X // Factor

a x0^2 + b x0 y0 + c x0 y0 + d y0^2

3、用Mathematica求a、b、c、d应该满足的关系：

Reduce[ForAll[{x0, y0}, x0*y0 != 0, X.A.X > 0 && Det[A] != 0]]

4、如果矩阵A是对称矩阵，结果可能会好一点：

A = {{a, b}, {b, d}}

Reduce[ForAll[{x0, y0}, x0*y0 != 0, X.A.X > 0 && Det[A] != 0]]

最后的结论是：

d>0且b^2>ad。

5、由于这是一个2*2的矩阵，那么，a和d的地位是等同的。

一般的，我满都从左上角开始，依次选取子矩阵，要求各个子矩阵的行列式大于0，所以，第四步的结论可以写为：

a>0且b^2>ad。

6、三维情况下，我们仍旧限定A是对称矩阵：

A = {{x, b, c}, {b, y, d}, {c, d, z}}

但是，Mathematica没有给出教材上那么整洁的充要条件。