【网络画板】用轨迹法作椭圆内的五边形封闭光路

1、首先，绘制椭圆。

这可以根据椭圆的第一定义作图：A、B为焦点、经过点C的椭圆。

2、取椭圆的右顶点D，在椭圆上取动点U，连接线段DU。

3、作椭圆在U点的切线u，

CD关于切线u的对称线为u'。

这样，u'就与CD的反射线在同一条直线上。

4、设直线u'与椭圆交于另一个点V，

UV就是DU在U的反射线。

5、作UV在V的反射线，记为VW；

6、设直线VW与直线AB交于X，

测量∠VAX的弧度m0；

设AB中点为Q，Q向V缩放，缩放比例为m0-pi/2，得到点Y。

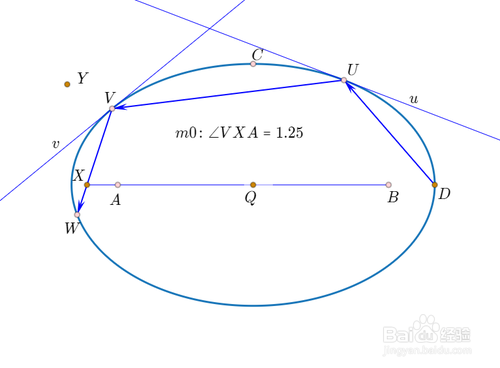
7、根据点U构造Y的轨迹，变量范围是0到pi，样本数定为6000。

如下图的红色曲线，就是所做的轨迹。

8、红色曲线以椭圆有三个交点，除了D以外，还有两个，分别记为M和N。

9、作ME垂直于直线AB，垂足为E；

以A、B为焦点，作经过E的椭圆，如图的绿色椭圆。

作NF垂直于直线AB，垂足为F；

以A、B为焦点，作经过F的圆锥曲线，如图的兰色曲线。

10、作绿色椭圆和原椭圆之间的Poncelet五边形，就是椭圆的五边形封闭光路。

这样的五边形封闭光路有无数个。

11、作兰色圆锥曲线与原椭圆之间的Poncelet五边形，得到的是五角星封闭光路。

这样的封闭光路也有无数个。

12、凸五边形封闭光路的周长为定值，

五角星封闭光路的周长也是定值，但大于凸五边形封闭光路的周长。

这可以测量知道，目前我没算出精确值。