【微分几何】怎么认识螺旋面？

1、作图工具是那款软件，不明就里的人，看代码。

点{1,0,0}绕z轴旋转v角度之后，再沿着z轴平移v/2个单位，就得到一条螺旋线：

{ Cos[v], Sin[v], v/2}

2、从z轴到这个螺旋线的直纹面，是一个螺旋面：

{ u Cos[v], u Sin[v], v/2}

3、以{1,0,0}为圆心、半径为1/2、垂直于y轴的圆，绕着螺旋线螺旋上升，就得到一个螺旋管：

{1/2 (2 + Cos[u]) Cos[v], 1/2 (2 + Cos[u]) Sin[v], 1/2 (v + Sin[u])}

4、但是，上述螺旋管与螺旋线的法平面的截线，不是标准圆形，而是一个扁椭圆。为了让截线是标准圆，特意使用如下圆：

{Cos[u]/2, -(Sin[u]/(2 Sqrt[5])), Sin[u]/Sqrt[5]}

得到的螺旋管是：

{1/10 (5 (2 + Cos[u]) Cos[v] + Sqrt[5] Sin[u] Sin[v]), 

 1/10 (-Sqrt[5] Cos[v] Sin[u] + 5 (2 + Cos[u]) Sin[v]), 

 v/2 + Sin[u]/Sqrt[5]}

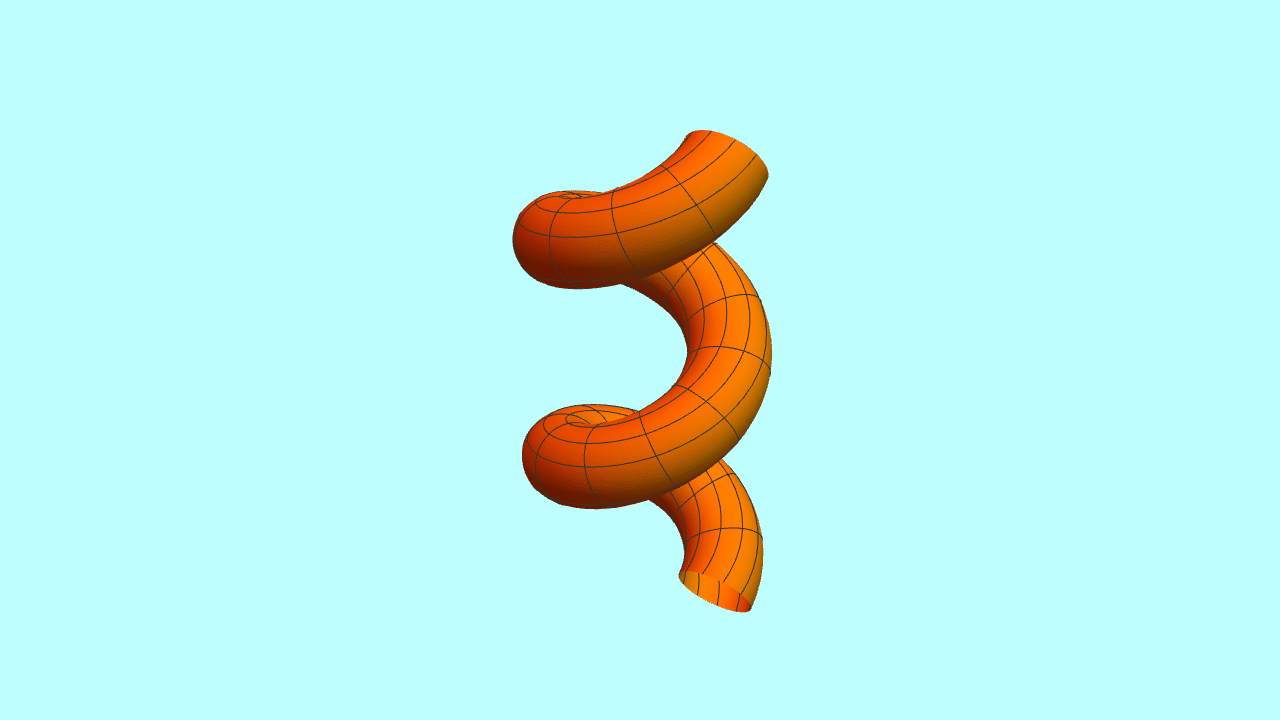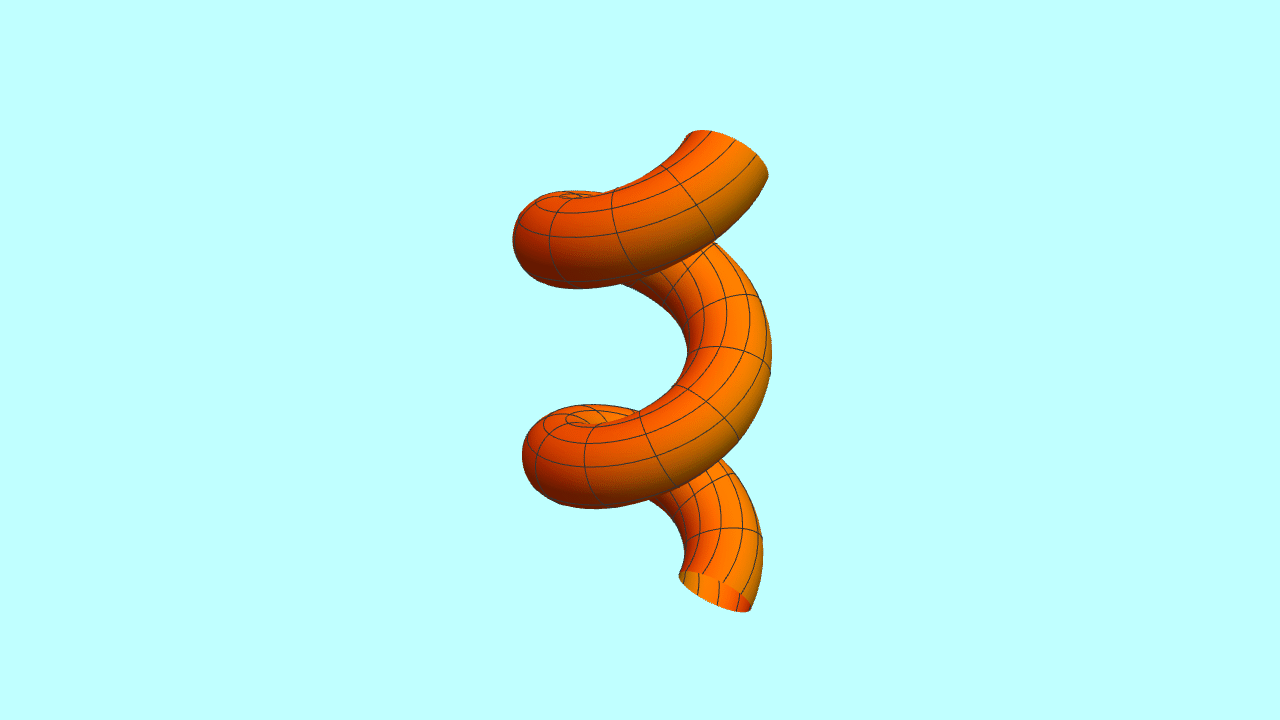
5、类似的，可以得到截面是正三角形的螺旋管。

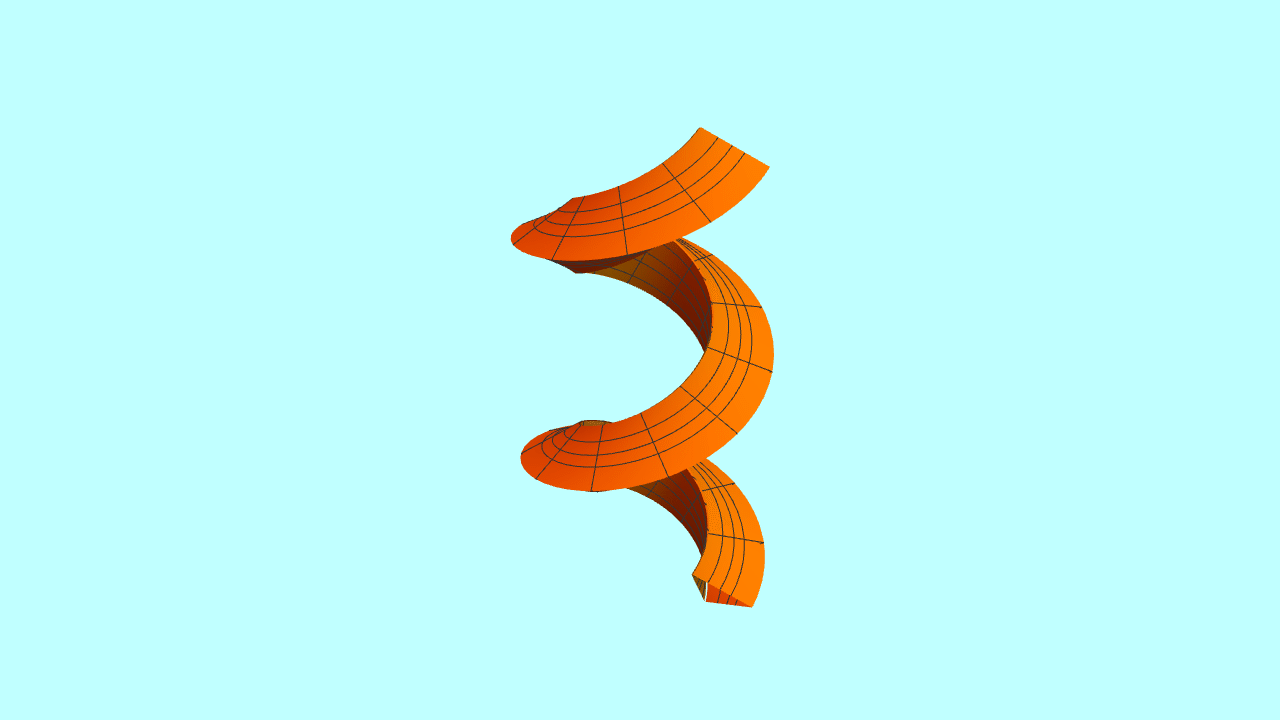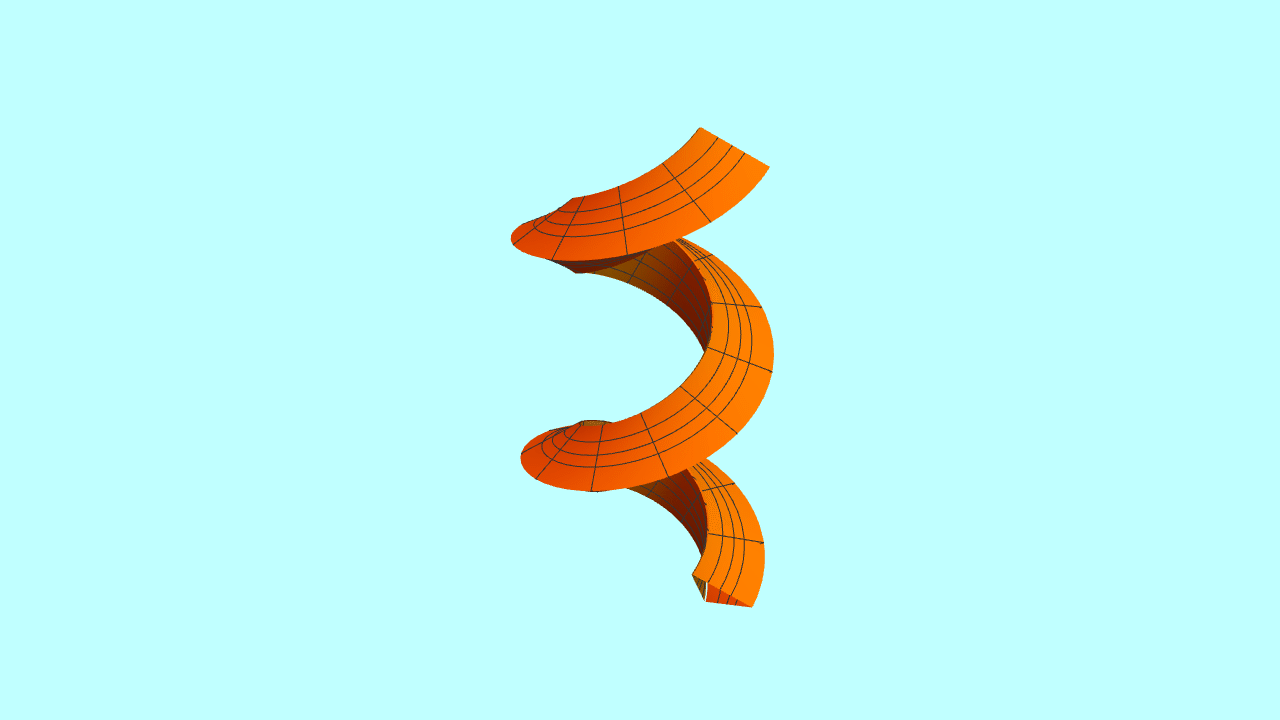
6、截面是三叶玫瑰线的螺旋管。