matlab一元多项式回归步骤及实例演示
1、一元多项式回归函数。
(1)[p,S]=polyfit(x,y,m) 确定多项式系数的 MATLAB命令
说明: x=(x 1,x 2 ,,,x n),y=(y 1 ,y 2,,,y n );p=(a 1,a 2,,,a m+1) 是多项式 y=a1xm+a2xm-1+,+a mx+am+1的系数; S 是一个矩阵 , 用来估计预测误差
(2)polytool(x,y,m) 调用多项式回归 GUI 界面,参数意义同 polyfit。
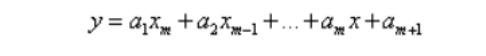
2、预测和预测误差估计。
(1)Y=polyval(p,x) 求 polyfit 所得的回归多项式在 x 处的预测值 Y ;
(2)[Y,DELTA]=polyconf(p,x,S,alpha) 求 polyfit 所得的回归多项式在 x 处的预测值 Y 及预测值的显著性为 1-alpha 的置信区间 Y±DELTA, alpha 缺省时为 0.5。
3、实例演示说明
观测物体降落的距离 s 与时间 t 的关系,得到数据如下表,求 s 的表达式 ( 即回归方程 s=a+bt+ct 2)
t (s) 1/30 2/30 3/30 4/30 5/30 6/30 7/30
s (cm) 11.86 15.67 20.60 26.69 33.71 41.93 51.13
t (s) 8/30 9/30 10/30 11/30 12/30 13/30 14/30
s (cm) 61.49 72.90 85.44 99.08 113.77 129.54 146.48
4、方法一:直接作二次多项式。
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
[p,S]=polyfit(t,s,2)
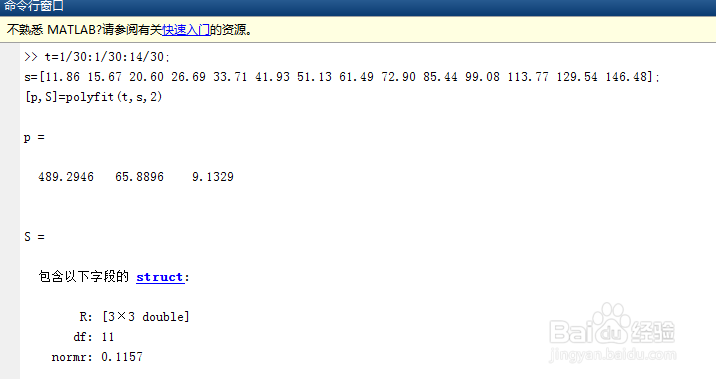
5、故回归模型为:
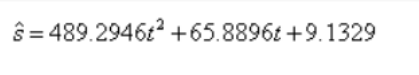
6、方法二:化为多元线性回归。
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
T=[ones(14,1) t' (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T)
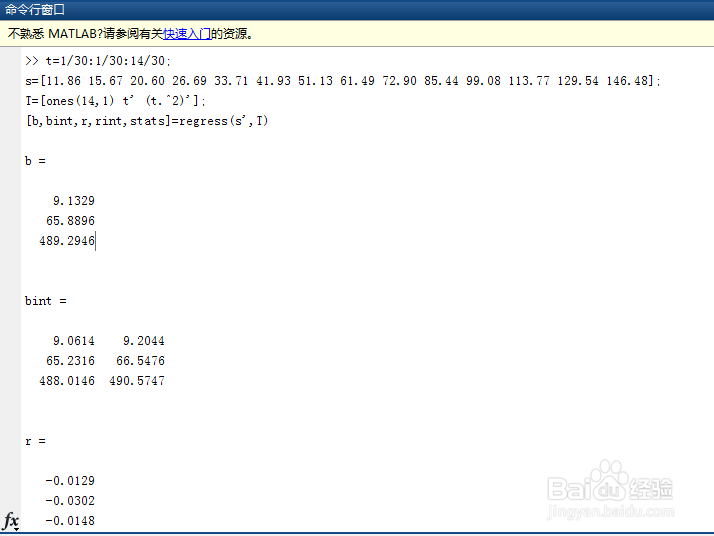
7、故回归模型为:
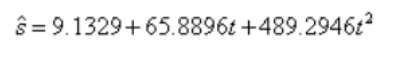
8、预测及作图。
Y=polyconf(p,t,S)
plot(t,s,'k+',t,Y,'r')
