Mathematica基础——三重积分
1、先来画图:
RegionPlot3D[x^2+y^2<=z<=1,{x,-1,1},{y,-1,1},{z,-0.5,1.5}

2、求zhege图形的体积:
Integrate[Boole[x^2+y^2<=z<=1],{x,-Infinity,Infinity},{y,-Infinity,Infinity},{z,-Infinity,Infinity}]

3、如果每一个点的密度都是该点的竖坐标,求这个“物体”的质量:
Integrate[z Boole[x^2+y^2<=z<=1], {x,-Infinity,Infinity}, {y,-Infinity,Infinity}, {z,-Infinity,Infinity}]

4、计算三重积分,题目如下图。
Integrate[(x^2+y^2) Boole[x^2+y^2<=4&&Sqrt[x^2+y^2]<=z<=2], {x,-Infinity,Infinity}, {y,-Infinity,Infinity}, {z,-Infinity,Infinity}]
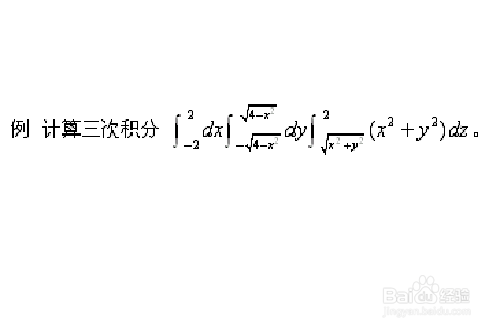

5、对Sqrt[x^2+y^2+z^2]求积分,积分区域是x^2+y^2+z^2<=z。
直接积分:
Integrate[Sqrt[x^2+y^2+z^2] Boole[x^2+y^2+z^2<=z ] , {x,-Infinity,Infinity}, {y,-Infinity,Infinity}, {z,-Infinity,Infinity}]

6、转而尝试球坐标变换:
令:{x->r Sin[u] Cos[v],y->r Sin[u] Sin[v],z->r Cos[u]}于是有:dx dy dz->(r^2)Sin[u] dr du dv
原题可以化为:
Integrate[r^2 Sin[u] Sqrt[x^2+y^2+z^2]/.{x->r Sin[u] Cos[v],y->r Sin[u] Sin[v],z->r Cos[u]},{v,0,2 Pi},{u,0,Pi/2},{r,0,Cos[u]}]
