怎样借助变量代换求解三角函数运算的题目?
1、引入题目:sin²10°+cos²40°+sin10°cos40°。
对于此类题目,如果积化和差或者和差化积不是很熟练的话,可以使用其他的方法进行求解。

2、变量代换的核心恒等式:
x=(x+y)/2+(x-y)/2;y=(x+y)/2-(x-y)/2.

3、由上面的恒等式,假设sin10°=M+N,cos40°=M-N.

4、则,
M =1/2·(sin10°+cos40°)
=sin30°cos20°
=1/2·cos20°

5、N =1/2·(sin10°-cos40°)
=-cos30°sin20°
=-√3/2·sin20°

6、原式=(M+N)²+(M-N)²+(M+N)(M-N)
=3M²+N²

7、所以,
原式=3/4·(sin²20°+cos²20°)=3/4 .
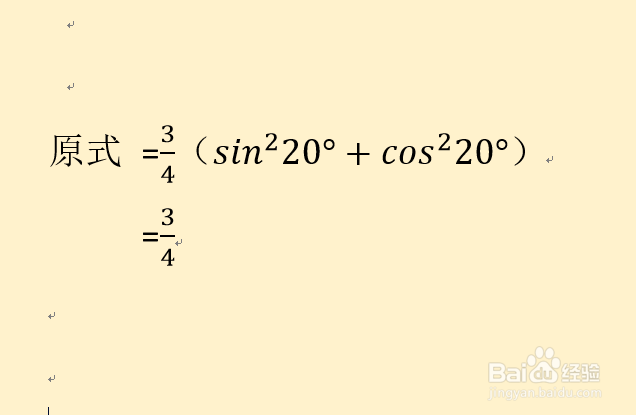
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。