【几何代数】怎么直观的理解单位双向量？

1、给定两个互相垂直的单位向量a和b，那么它们围成的矩形面积等于1。

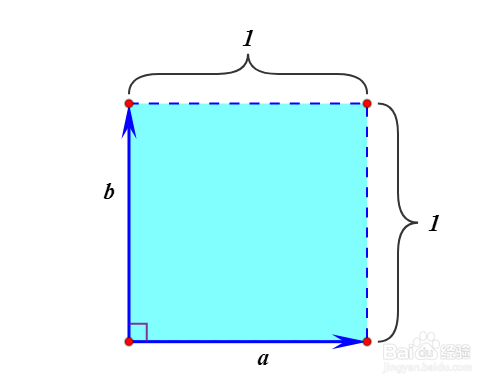
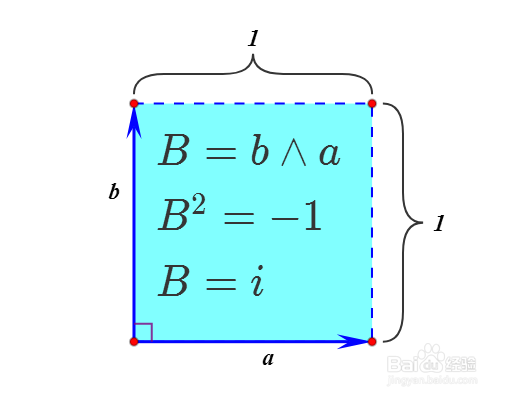
2、把有向面积记为：

B=b∧a

注意：

a到b需要逆时针旋转90°；

单位有向面积B表示的是图中矩形的逆时针面积，大小为1，符号为-。

3、所以，可以把单位有向面积B视为虚数单位i。

.

从这一刻起，把单位双向量记为i。

4、因为有向面积只有两个方向，因此，可以把单位双向量视为旋转算子。

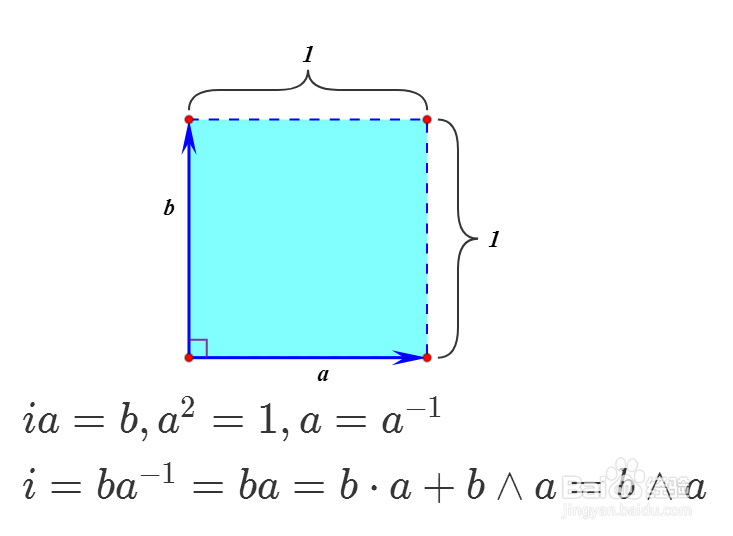
实际上，i左乘向量a，表示把a逆时针旋转90°:

ia=b

也就是说，单位双向量是90°的旋转算子。

5、注意到a和b是垂直的，所以：

a·b=0

进而：

i=b∧a=ba。

6、如果单位向量a逆时针旋转θ，到达向量b的位置，那么，几何积就可以表示为角度为θ的旋转算子：