第二种搜寻水仙花数的Mathematica算法

1、前文的代码，来寻找七位数的水仙花数：

Table[If[({a, b, c, d, e, f, g}^7 // Total) == 

      FromDigits[{a, b, c, d, e, f, g}], 

     FromDigits[{a, b, c, d, e, f, g}], 0], {a, 1, 9}, {b, 0, 9}, {c, 

     0, 9}, {d, 0, 9}, {e, 0, 9}, {f, 0, 9}, {g, 0, 9}] // Flatten // 

  Union // AbsoluteTiming

耗时超过20秒。

2、本文的代码，需要构造一个自定义函数：

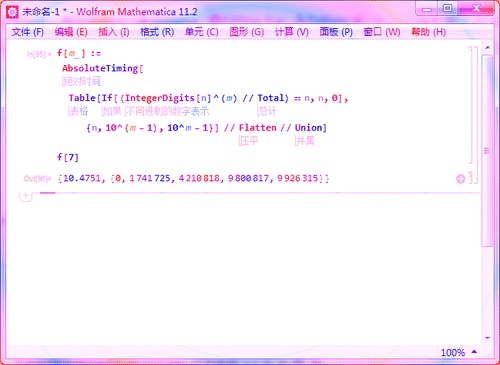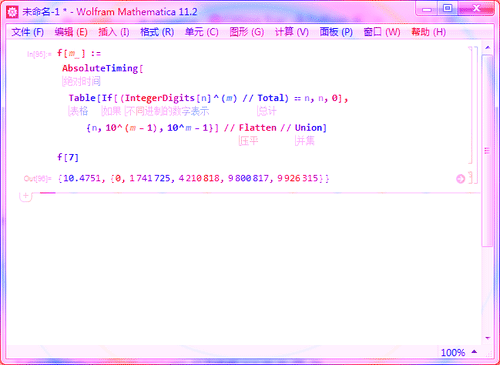
f[m_] := AbsoluteTiming[

  Table[If[(IntegerDigits[n]^(m) // Total) == n, n, 0], {n, 

      10^(m - 1), 10^m - 1}] // Flatten // Union]

其中，m就是控制数位的变量，比如，f[7]就可以得到所有的七位数的水仙花数，耗时也较少。

3、IntegerDigits[n]

把整数n拆分成单个数字，此时的n必须是整数；

如果是负数，负号会被忽略。

4、仍旧是用If语句进行甄别和筛选，但是，当位数超过7以后，耗时明显增加了一大截。

下面列出3位数到7位数的所有水仙花数：

f[#]&/@Range[3,7]

5、如果先针对个位数进行判断，或许会容易不少；

注意到n^8的个位数只能是0，1，5，6：

Table[IntegerDigits[n^8][[-1]], {n, 1, 10}]

6、这样，无需计算数字的8次方，只需要判断数字是不是2和5的倍数，就可以知道n^8的个位数字：

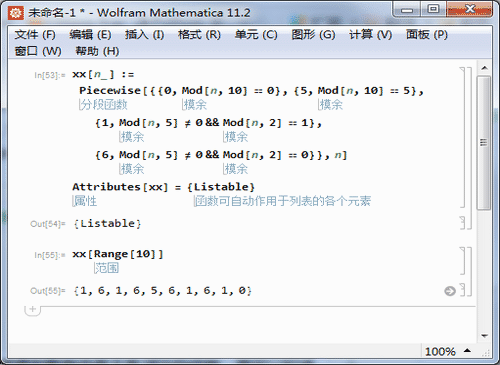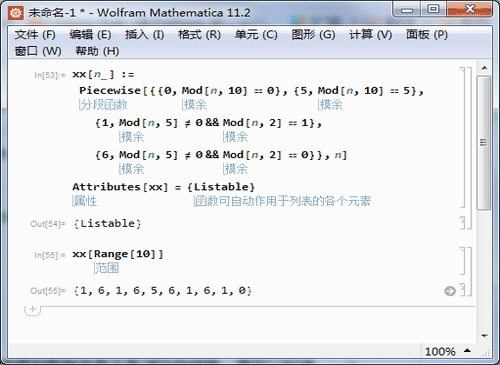
xx[n_] := 

 Piecewise[{{0, Mod[n, 10] == 0}, {5, Mod[n, 10] == 5}, {1, 

    Mod[n, 5] != 0 && Mod[n, 2] == 1}, {6, 

    Mod[n, 5] != 0 && Mod[n, 2] == 0}}, n]

7、于是，把算法进一步修改为：

AbsoluteTiming[

 Table[If[u[Total[xx[IntegerDigits[n]]]] == u[n], 

    If[(IntegerDigits[n]^8 // Total) == n, n, 0], 0], {n, 10^7, 

    10^8 - 1}] // Union]

也还是很慢，半天没出结果。