怎么计算一般三角形的隐函数方程?
1、想求出以{0, 0}, {1, 0}, {0, 1}为顶点的等腰直角三角形的隐函数方程,就先确定{0, 0}, {1, 0}, {0, 1}到{-1, 0}, {1, 0}, {0, Sqrt[3]}的仿射变换的规则:
v={-1 + 2*x + y, Sqrt[3]*y}

2、这样,可以求出这个等腰直角三角形的隐函数方程。
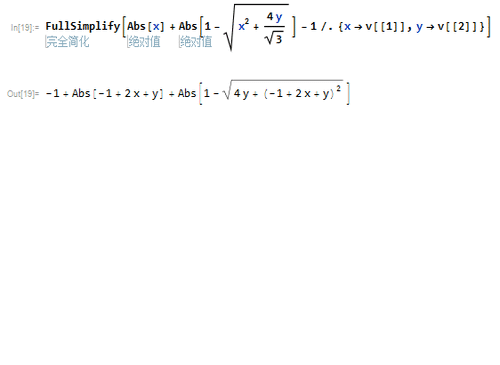
3、作出图像。
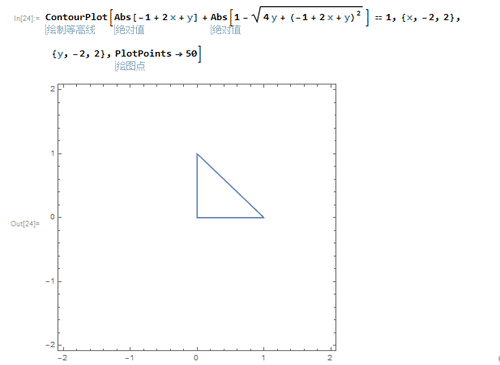
4、其实,三点到三点的对应关系,可以稍微颠倒一下顺序:
a = {{-1, 0}, {1, 0}, {0, Sqrt[3]}};
p = {{0, 0}, {0, 1}, {1, 0}};
这样,就可以得到上面等腰直角三角形的另一个隐函数方程。

5、可以发现,这两个隐函数的图像是完全重合的。
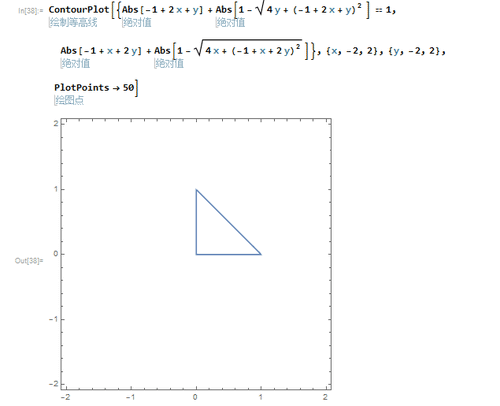
6、用这个方法,可以求出以{m0, m1}, {m2, m3}, {m4, m5}为顶点的三角形的隐函数方程。
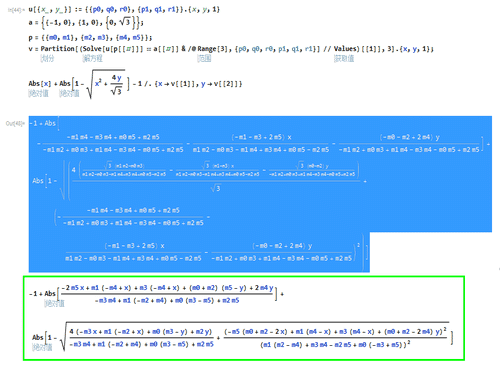
7、打开网络画板,绘制三个自由点A、B、C,并测量三个点的横纵坐标:
m0, m1,m2, m3,m4, m5,
然后绘制上面的隐函数方程。

声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:182
阅读量:58
阅读量:195
阅读量:96
阅读量:188