矩阵乘积与双线性型的关系

1、给定两个三维空间的向量A和B。

这两个向量是相对于标准正交基而言的。

2、给出一个双线性型：

f[X_, Y_] := 2 X.Y

这样，f[A,B]就代表一个具体的数字。

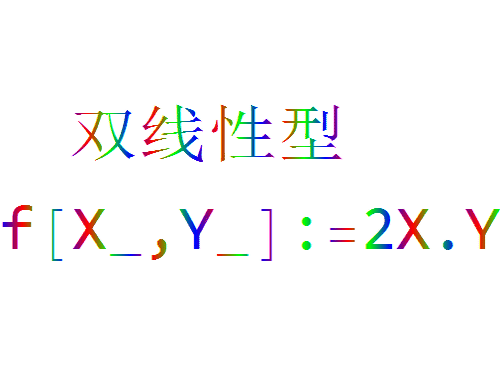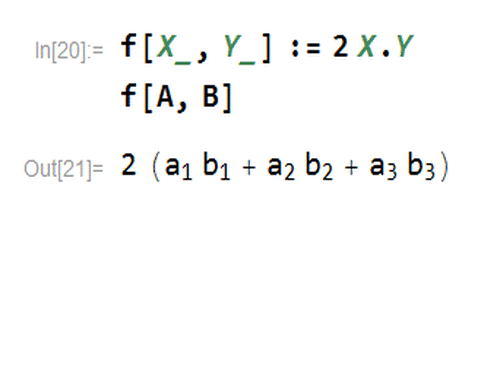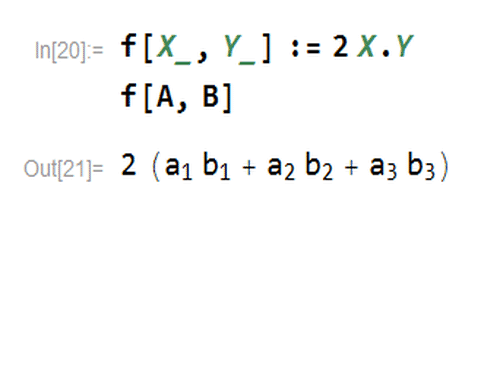
3、双线性型关于标准正交基的矩阵是：

K={{2, 0, 0}, {0, 2, 0}, {0, 0, 2}}

4、这个双线性型可以写成矩阵乘积的形式：

f[A,B]=A.K.B

5、给出一个新的基：

基'={U,V,W}//Transpose;

其中：

U = Table[Subscript[u, n], {n, 3}];

V = Table[Subscript[v, n], {n, 3}];

W = Table[Subscript[w, n], {n, 3}];

6、假设在这个新基之下，A和B的坐标向量是A0和B0，那么：

A=基0.A0

B=基0.B0

7、记双线性型关于基0的矩阵是K0。

8、那么，双线性型可以写为矩阵乘积的形式：

f[A,B]=A0.K0.B0

额，这一步的验证，Mathematica出现了卡顿，半个小时都没有化简出结果。