【Mathematica】复数二次开方的位置如何确定？

1、直接用Mathematica给出Sqrt[z]的显式实部和虚部，是行不通的，即使严格指定a和b是实数，也不行：

Sqrt[a + b I] // ReIm

Refine[ReIm[Sqrt[a + b I]], Element[{a, b}, Reals]]

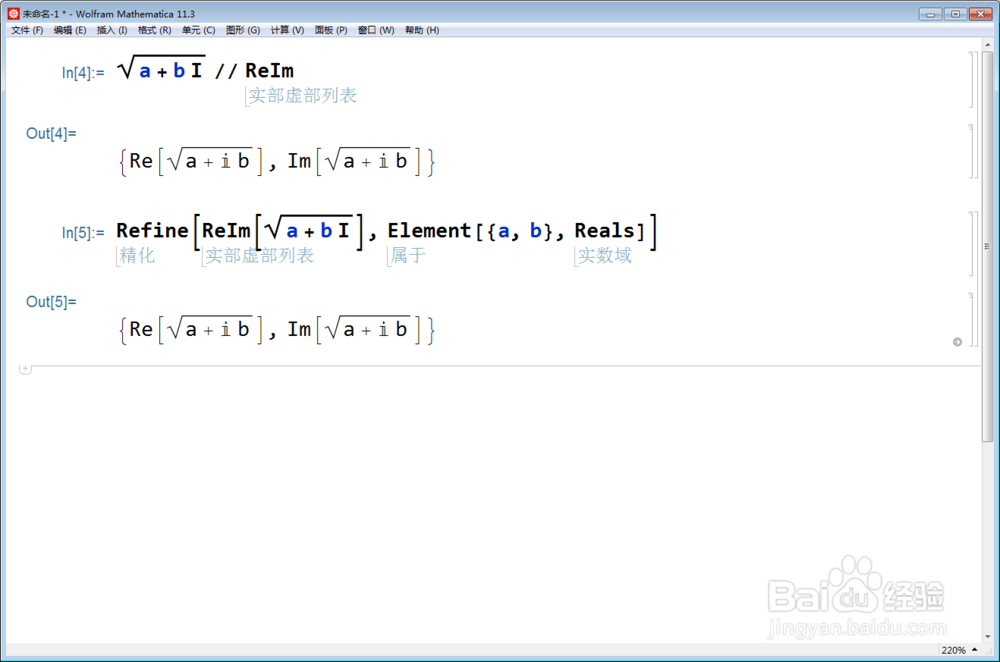
2、假设Sqrt[z]=x+y*I，其中x和y是实数，那么必有：

z=(x+y*I)^2

展开，有：

(x + y*I)^2 // Expand

3、注意了：

a+b*I=x^2 - y^2+ 2*I*x*y 

等式两边的实部和虚部应该分别相等，这就确定一个方程组。

解这个方程组：

sol=Solve[{x^2 - y^2 == a, 2 x y == b}, {x, y}] // FullSimplify

4、得到四组解，但是注意到x必须是实数。

.

而当a和b都是非零实数的时候，Sqrt[a - Sqrt[a^2 + b^2]]不是实数。

因此可以把前两个解排除：

sol=Solve[{x^2 - y^2 == a, 2 x y == b}, {x, y}][[3;;]] // FullSimplify

5、这样，复数的二次开方Sqrt[z]，得到两个不同的复数，它们的实部和虚部，分别如下：

sol// Values

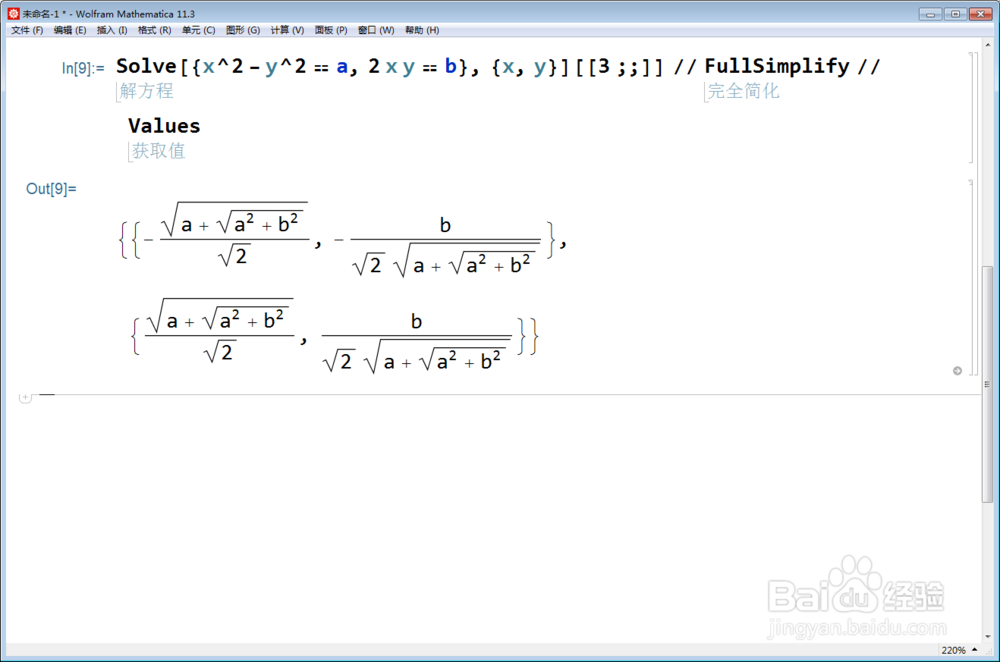
6、这两个点是关于原点对称的：

7、读者可能会有疑问：

Sqrt[z]对应两个复数，那么-Sqrt[z]也对应两个复数。

如此一来，岂不是有四个复数了？

其实，还是两个，因为Sqrt[z]和-Sqrt[z]也关于原点对称啊。

1、给定复变函数f[z_]:=z^2+a+b*I （z是复数变量，a和b是实数定值，I是虚数单位）。

考虑f[z]的不动点，也就是解方程：

Solve[f[z] == z, z] // FullSimplify

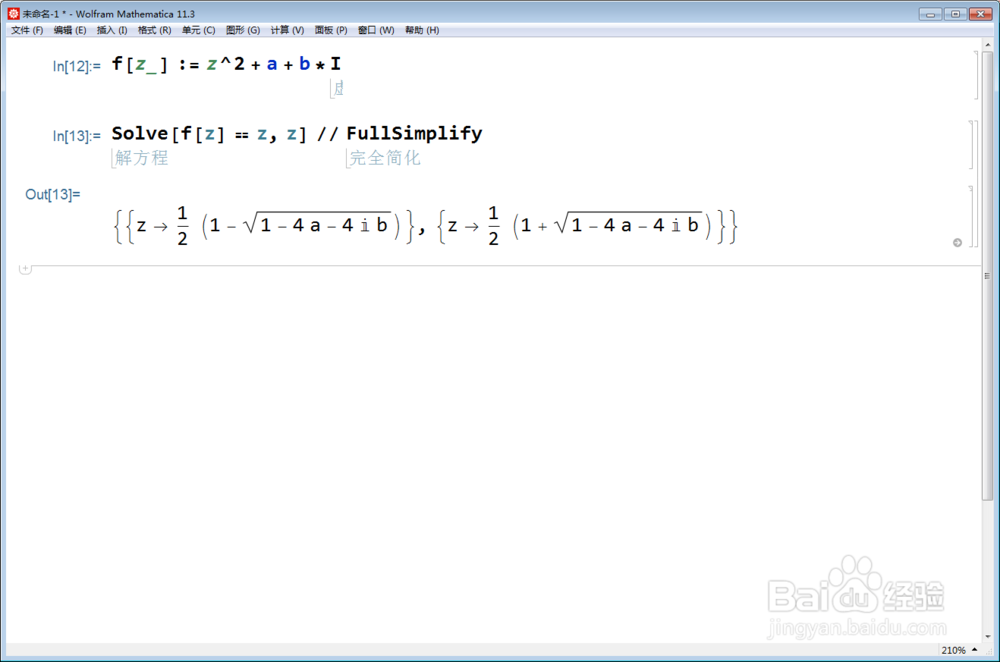
2、得到的结果，带有二次开方的复数，套用上一节的方法：

sol = Solve[

     {x^2 - y^2 == 1 - 4*a, 2*x*y == -4*b}, {x, y}][[3 ;;]] // FullSimplify

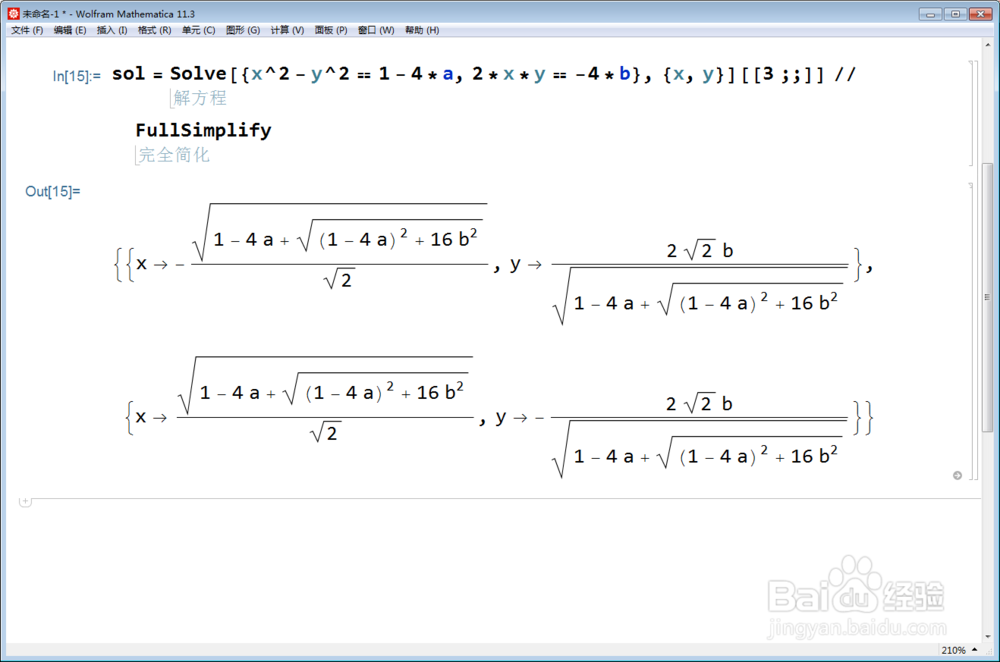
3、这样，就得到两个不动点：

1/2 (1 - (x + y*I)) /. sol // FullSimplify

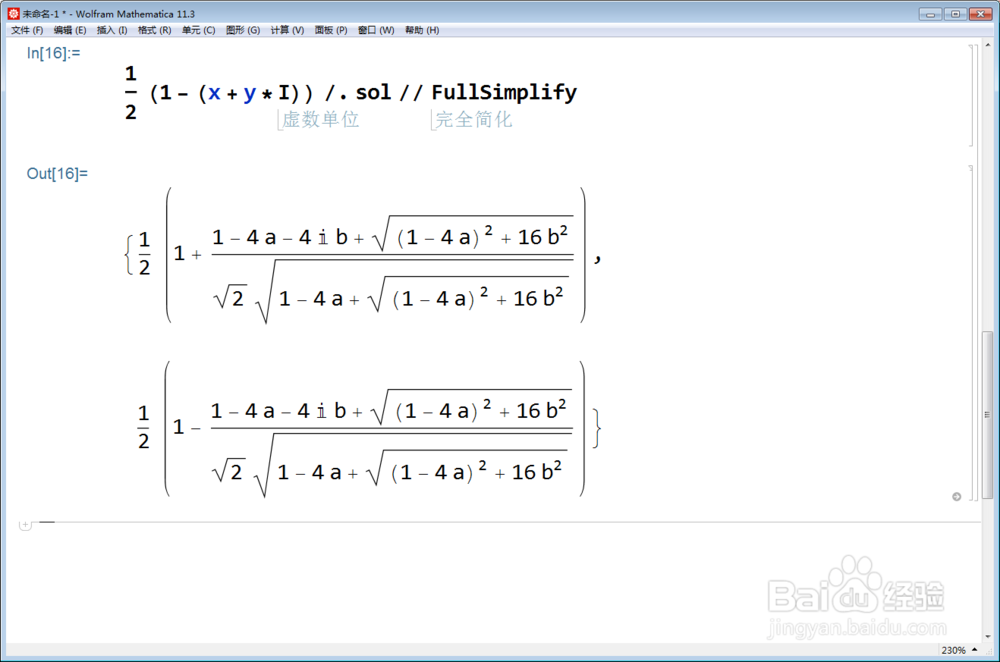
4、也可以分别提取出这两个不动点各自的实部和虚部：

1/2 (1 - {x, y}) /. sol // FullSimplify

这样是为了便于在【网络画板】或【几何画板】里面，进行【尺规作图】。