求最小的公倍数 方法总结

1、以求4、6、16的最小公倍数为例。

先找出4、6、16的最小公因数，列短除式。

用三个数的最小公因数2去除这几个数，得到三个商2、3、8。

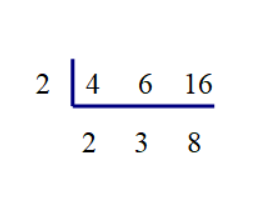
2、找出三个商2、3、8的最小公因数2，用最小公因数去除这几个商，得到新一级的商1、3、4。

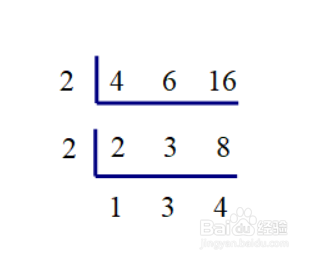
3、以此类推，直到最后所得的商互质（即几个商只有公因数1）为止。

4、将所有的公因数以及最后所得的几个商相乘，所得积就是我们要求的几个数的最小公倍数。

1、由于：两个数的乘积等于这两个数的最大公约数与最小公倍数的积。

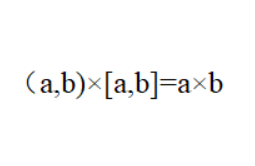
2、所以，求两个数的最小公倍数，就可以先求出它们的最大公约数，然后利用上述公式求出它们的最小公倍数。

以8和20为例，计算过程如图：

1、把一个合数分解成若干个质因数乘积的形式，即求质因数的过程，称为分解质因数。

分解质因数的算式为短除法。原理相同，形式有所不同。

公式如下图：

2、以18和30为例，先将18和30分解质因数。

（在数比较简单的情况下，无需运用短除列式。）

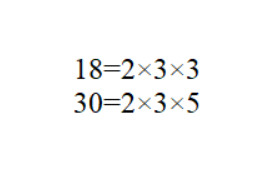
3、公有的质因数为2和3，独有的质因数为3和5。

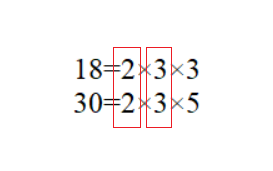
4、所以可得出18和30的最小公倍数为2×3×3×5=90。