matlab常微分方程的差分方程如何代码实现

1、向后euler法由于等式前后都有u[n+1],所以，不能向向前euler法一样，只需要做出循环：u[n+1]=u[n]+h*f(t[n],u[n])即可。

2、所以，向后euler在进行计算u[n+1]时，需要设定u_[n+1]^{0}，和精确误差eps，利用差分方程进行迭代，使得在迭代前后值误差足够小的时候，认为已经收敛到局部精确解。

1、对已知、所需的条件进行设定：

h是等距差分的间距；eps是迭代的精度，可根据要求进行更改。

u(1)=初始条件。以u=exp(-t)为例。

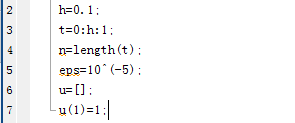
2、迭代部分：

temp是迭代后的值，用于比较差是否小于误差精度。

3、由于判断收敛的条件有两个值，所以需要在for循环内预设。由于while循环内的语句，所以，temp的值的关键，而u[i]的值仅需设定成temp-c即可。（c是任一大于eps的常数。）

由于向后euler恒稳定，迭代收敛，temp的值可以设定任意常数，但是误差会有很大区别。所以使用向前euler法设定的temp的值。