二叉搜索树使用c++语言如何实现删除节点的操作
1、第一步简单介绍一下什么是二叉搜索树(Binary Search Tree)。二叉搜索树是二叉树的一种,一个节点最多只有两个子节点,但是节点的左子节点的值要小于节点的值,节点右子节点的值要大于节点的值。

2、删除操作需要针对子节点个数进行讨论。
1、如果一个节点的子节点个数为0,就可以直接删除这个节点

3、如果这个节点的子节点个数是一个,那么就需要再删除该节点之后,将该节点的子节点和父节点连接到一起。
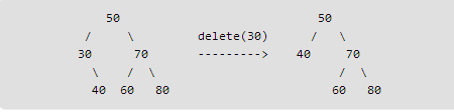
4、如果该节点的子节点个数为两个,那么这个情况比较复杂。这个时候需要在该节点的右子树中找到最小的节点来替代该节点。这一步的操作需要通过递归来实现。具体代码看下一步。

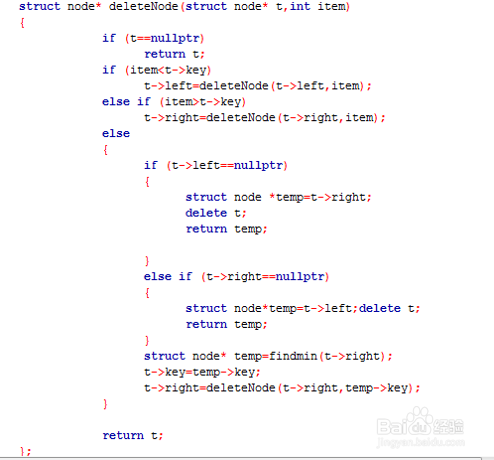
5、光说不做不行,这一步我们将展示上述三步的具体代码实现过程。下图所提供的代码是一个类的方法。仅供参考。
6、为了整个程序的完整性,这一步骤,我们提供整个二叉搜索树的实现代码,包括搜索、插入、删除、寻找最大最小值。如下:
#include <iostream>
using namespace std;
//tree node
struct node
{
int key;
struct node *left,*right;
};
//construct new node
struct node* newnode(int item)
{
struct node* temp=new node;
temp->key=item;
temp->left=nullptr;
temp->right=nullptr;
return temp;
};
//inorder travel
void inorder(struct node* root)
{
if (root!=nullptr)
{
inorder(root->left);
cout<<root->key<<endl;
inorder(root->right);
}
}
class BinarySearchTree
{
public:
BinarySearchTree(){root=nullptr;};
//find the minimum value
struct node *findmin(struct node*t)
{
if (t==nullptr)
return nullptr;
if (t->left==nullptr)
return t;
else
findmin(t->left);
};
//find a maximum value
struct node*findmax(struct node*t)
{
if (t==nullptr)
return nullptr;
if (t->right==nullptr)
return t;
else
findmax(t->right);
};
//if a node in Binary search tree
bool contains(struct node* t,int item)
{
if (t==nullptr)
return false;
else if (item>t->key)
contains(t->right,item);
else if (item<t->key)
contains(t->left,item);
else
return true;
}
//delete a node
struct node* deleteNode(struct node* t,int item)
{
if (t==nullptr)
return t;
if (item<t->key)
t->left=deleteNode(t->left,item);
else if (item>t->key)
t->right=deleteNode(t->right,item);
else
{
if (t->left==nullptr)
{
struct node *temp=t->right;
delete t;
return temp;
}
else if (t->right==nullptr)
{
struct node*temp=t->left;delete t;
return temp;
}
struct node* temp=findmin(t->right);
t->key=temp->key;
t->right=deleteNode(t->right,temp->key);
}
return t;
};
//insert a node
struct node* insert(struct node* t,int item)
{
if (t==nullptr&&root==nullptr)
{
root=newnode(item);
return root;
}
if (t==nullptr &&root!=nullptr)
return newnode(item);
if (item<t->key)
t->left=insert(t->left,item);
if (item>t->key)
t->right=insert(t->right,item);
root=t;
return root;
}
struct node* root;
};
int main()
{
BinarySearchTree tr;
tr.insert(tr.root,60);
tr.insert(tr.root,10);
tr.insert(tr.root,20);
tr.insert(tr.root,30);
tr.insert(tr.root,500);
tr.insert(tr.root,40);
cout<<"inorder travel "<<endl;
inorder(tr.root);
cout<<"if contains 10: "<<endl;
cout<<tr.contains(tr.root,10)<<endl;
cout<<"findmin "<<tr.findmin(tr.root)->key<<endl;
cout<<"delete 40 "<<endl;
tr.deleteNode(tr.root,40);
inorder(tr.root);
return 0;
}
