网络画板“仿射变换”功能的探索

1、        作三角形，并选中三角形的三个顶点和三条边；

        点击“仿射变换”选项；

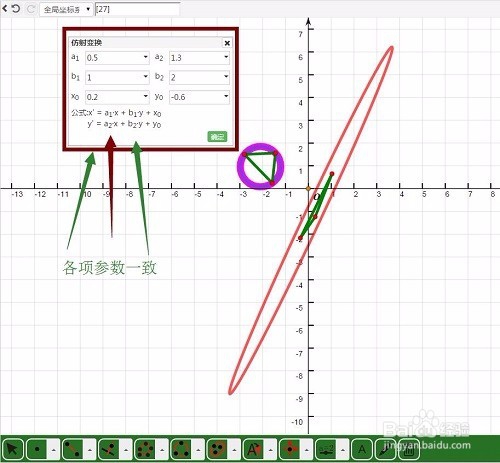
        设置参数，令x'=0.5x+y+0.2，y'=1.3x+2y-0.6；

        确定。

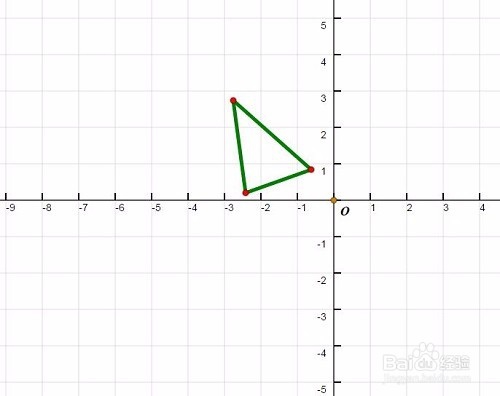
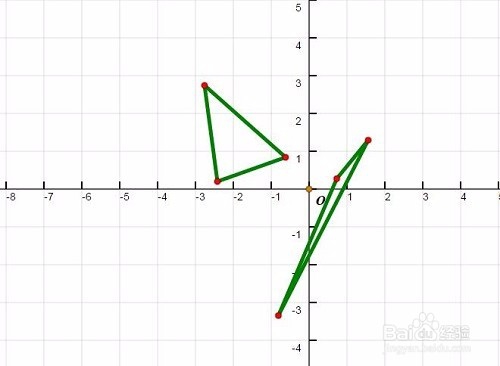
2、        尝试去拖动三角形的各个顶点，变换对象也会随之运动！

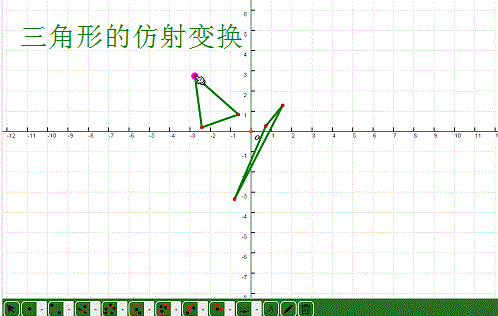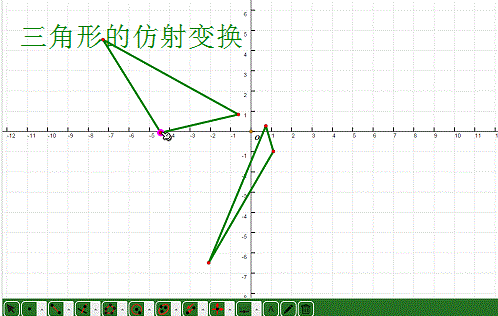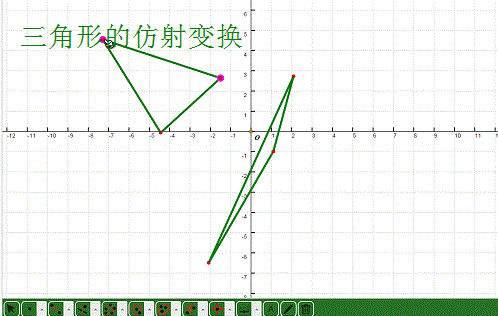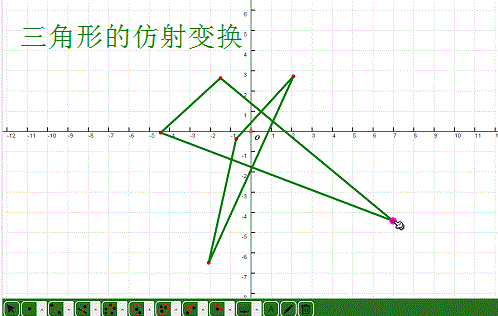
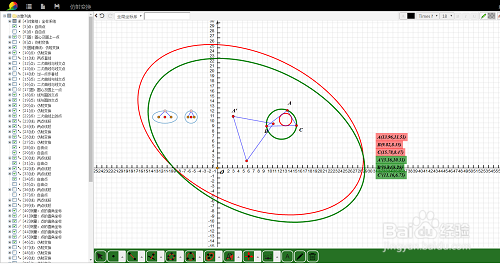
3、        作出原三角形的外接圆，看看这个圆的仿射变换是什么模样？

        奇怪的是，虽然得到一个椭圆，但这个椭圆却不是变换出来的三角形的外接椭圆。不明白了！

        这好像是个BUG！

1、        我个人感觉，用坐标来量化“仿射变换”的参数，有时候是不太方便的！ 比如，我们要作某个三角形的最大面积的内切椭圆的时候，不容易确定相应的仿射变换的参数！

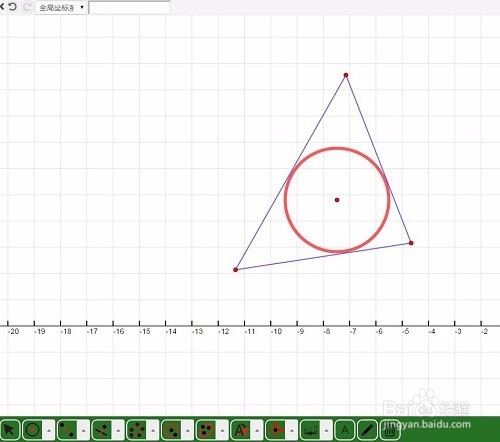
2、        先作出两个三角形ABC和A'B'C'，怎么实现三角形ABC到三角形A'B'C'的仿射变换？

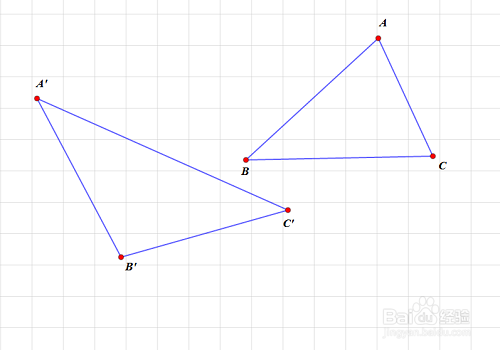
3、        求出A、B、C和A'、B'、C'的坐标：

        把鼠标光标放到B'上，点击鼠标右键，选择“坐标”选项，出来的就是它的坐标！

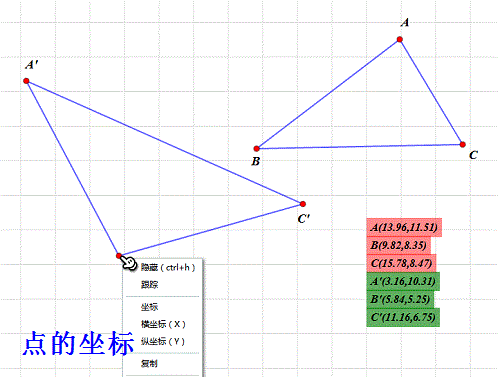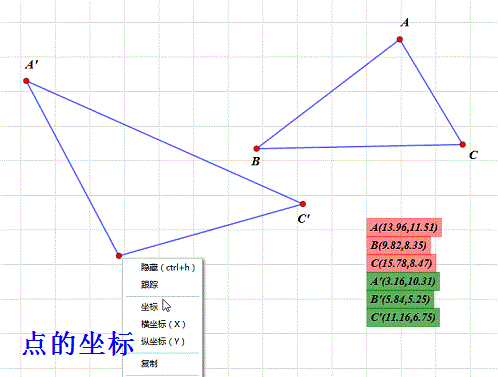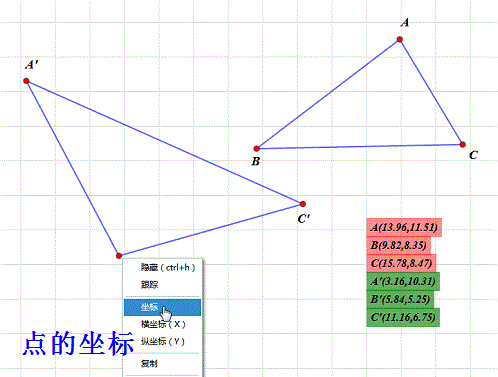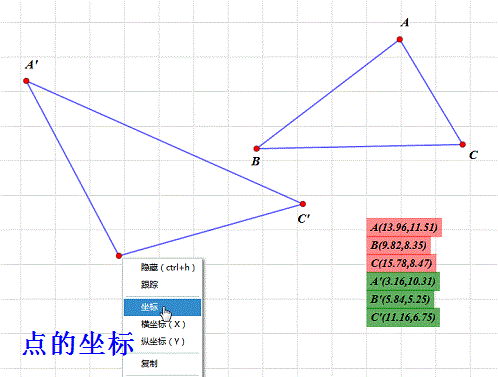
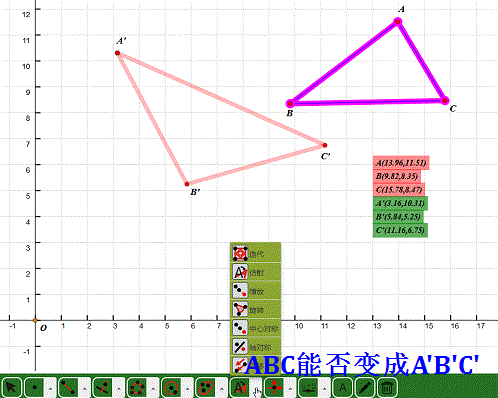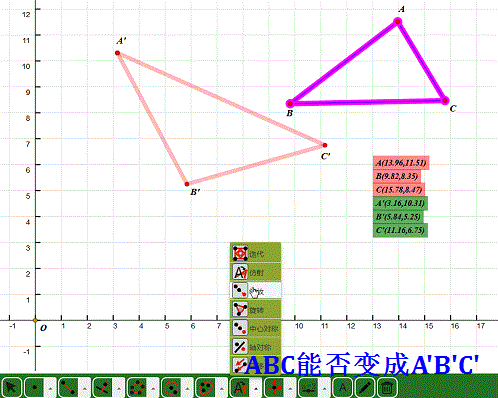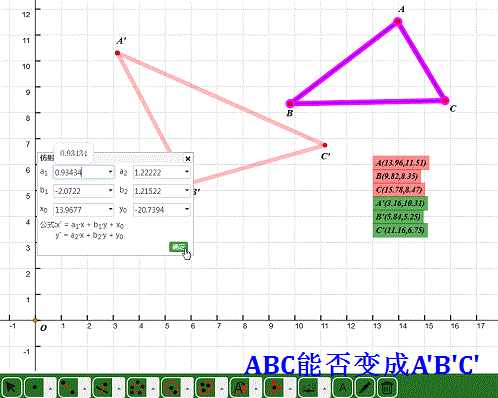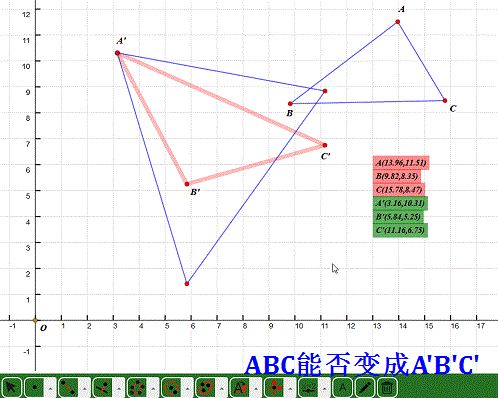
4、        把A、B、C和A'、B'、C'的坐标的坐标带入方程组里面，得到一个六元一次方程组，未知数是a1,a2,b1,b2,x0,y0。

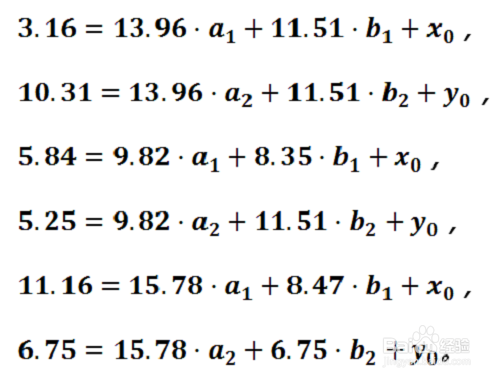
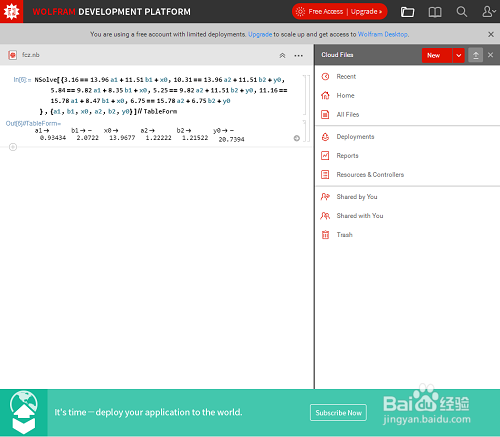
5、        大家发挥实力，借这个方程组。我就用Mathematica代劳了：

NSolve[{3.16==13.96 a1+11.51 b1+x0,10.31==13.96 a2+11.51 b2+y0,5.84==9.82 a1+8.35 b1+x0,5.25==9.82 a2+11.51 b2+y0,11.16==15.78 a1+8.47 b1+x0,6.75==15.78 a2+6.75 b2+y0 },{a1,b1,x0,a2,b2,y0}]

        结果答案是：

a1=0.93434

b1=-2.0722

x0=13.9677

a2=1.22222

b2=1.21522

y0=-20.7394

6、        选择整个三角形ABC，把诸参数带入到仿射变换对话框里面，点击“确定”，结果得到图中的另一个三角形，误差很大。这大概是求值误差导致的！

        注意，此过程中不要改变三角形ABC的位置！

7、        再来看看三角形ABC的内切圆和外接圆在同一个仿射变换下，会发生什么变化！

        作出三角形ABC的内切圆、外接圆；

        选择这两个圆，作仿射变换；

        结果如图！看来，网络画板的仿射变换功能还很不成熟！

        不过，有一个发现：网络画板的仿射变换，原图和变换图的颜色、线型等属性是一样的！红色对应红色，绿色对应绿色！