如何采用MATLAB计算一型曲面积分

1、阐述问题：

2、一型曲线积分的一般求解方法：

    其基本原理仍然是消元法。

3、求解问题的实例：

     由于要用到很多的公式编辑，这里就用截图的方式了。

4、求解分析：

    有问题可知，该积分分为两个连续的曲面组成，要对两个曲面分别求解积分的，然后相加，得到最后的积分效果。

1、打开软件：

    如图所示打开MATLAB软件，并且采用

      clear

      clc

     这两个命令进行清空工作空间和主页面；

2、定义符号变量：

  这里要用的x y z三个变量，采用以下指令进行计算可以得到：  

  syms x y z

;

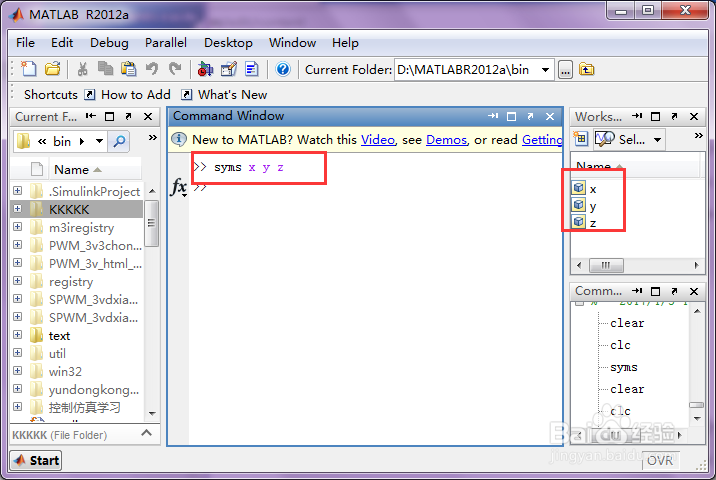
3、定义曲面约束程：

   第一个曲面约束方程是z=1，x*x+y*y<=1

   第二个方程是z=sqrt（x*x+y*y）<=1;

   采用以下代码实现：

    z1=1

    z2=sqrt(x*x+y*y)

4、计算面积微元：

    分别计算每一个平面的微元：

    d_z1=sqrt(1+diff(z1,x)^2+diff(z1,y)^2)

    d_z2=sqrt(1+diff(z2,x)^2+diff(z2,y)^2) 

5、计算二重积分1：

    经过微元化以后就可以分别计算两个区域的二重积分，对于二重积分的计算可以参考经验：如何采用电脑MATLAB软件求解多重积分。

对于第一个面因为是平面圆根据其计算方法可知，计算代码如下：

syms r q

frq=r^2*r

s1=int(1,q,0,2*pi)*int(frq,r,0,1)

  ；

6、计算二重积分2：

   根据积分的性质同样可以采用以下代码求解第二部分的积分值：  

   根据这一段代码得到二重积分的函数： 

   f=x^2+y^2;

    f2=simplify(f*d_z2)

  根据这一段代码求解二重积分：  

 syms r q

f2=r^2*r*2^(1/2)

s2=simplify(int(1,q,0,2*pi)*int(f2,r,0,1))

7、计算总面积：

    采用以下代码计算积分的总值如下：

    s=s1+s2。

8、总结：

   累死了，终于把这个是实验结束了，希望会对你有用了。