如何计算∫sinx^(1/a)dx的不定积分

1、本步骤，介绍∫sinx^(1/2)dx的计算过程：

2、步骤主要思路为：将x^(1/2)换元成t，然后再1次分部积分法。

1、本步骤，介绍∫sinx^(1/3)dx的计算过程：

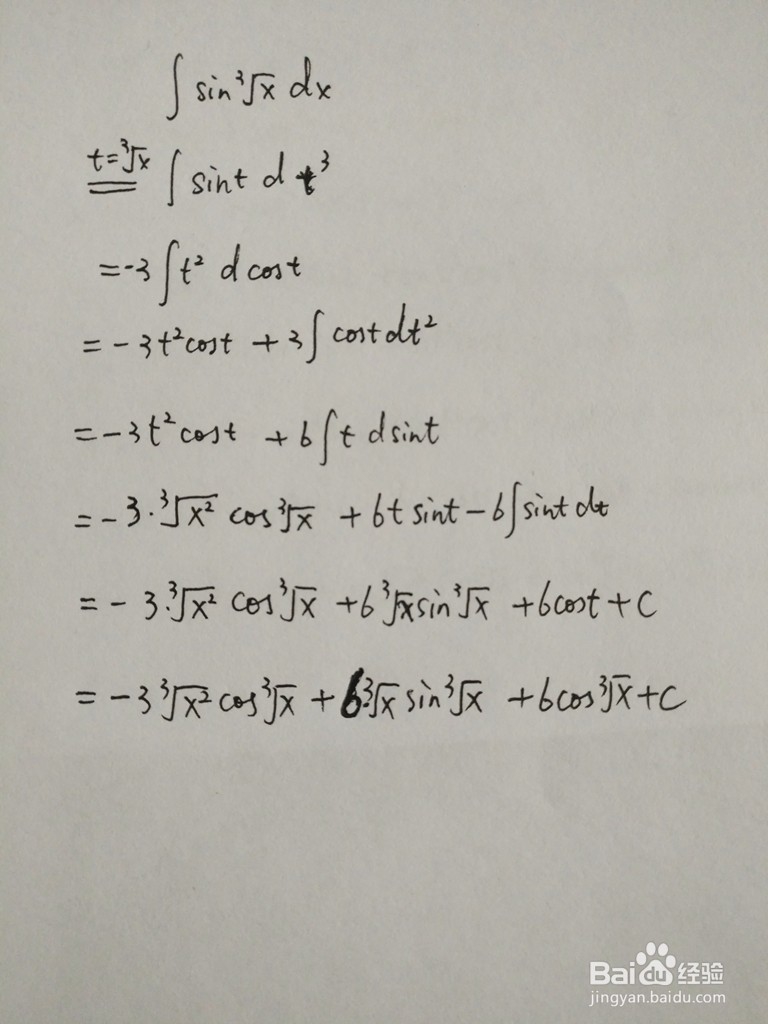
2、步骤主要思路为：将x^(1/3)换元成t，然后再2次分部积分法。

1、本步骤，介绍∫sinx^(1/4)dx的计算过程：

2、步骤主要思路为：将x^(1/4)换元成t，然后再3次分部积分法。

1、本步骤，介绍∫sinx^(1/5)dx的计算过程：

2、步骤主要思路为：将x^(1/5)换元成t，然后再4次分部积分法。

1、本步骤，介绍∫sinx^(1/6)dx的计算过程：

2、步骤主要思路为：将x^(1/6)换元成t，然后再5次分部积分法。

1、分部积分主要是通过函数乘积的导数，推广证明而来:

1、对于求形如∫x^(1/a)cosxdx的不定积分，其主要步骤如下：

2、1.首先用换元法，设t=x^(1/a)，则x=t^a.

3、2.代入到不定积分表达式中，得到含有三角函数和幂函数乘积形式为∫sintdt^a

4、3.将dt^a转换成at^(a-1)dt

5、4.后续根据函数中a的数值，将三角函数costdt变成dsint，或者sintdt变成-dcost形式，进行分部积分，即可得到结果。