化简二次根式之前学过什么

化简二次根式之前学过平方，开平方与平方运算互为逆运算。

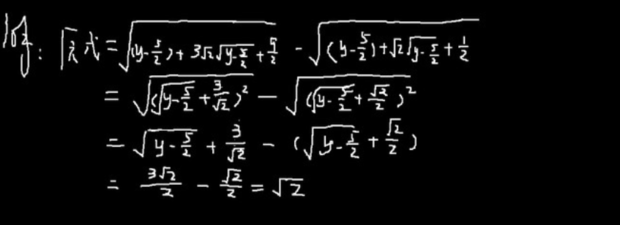
二次根式化简的基本方法：

1、根号下是一个正整数。

将该数字拆分成一个完全平方数和某个数字的乘积，然后将完全平方数开平方放到根号外面。

2、根号下是一个分数。

将该分数拆分成一个分数的平方数和某个数字的乘积，然后将分数开根号到根号外面。

3、根号下有数字和字母。

这种情况下，由于不确定字母是正数还是负数，因此开放的时候要带着绝对值开方。

4、两个根式相加减。

首先将两个根式通分，然后再运算。

数学常用的解决技巧：

1、配方法。

所谓配方，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和形式。

通过配方解决数学问题的方法叫配方法。其中，用的最多的是配成完全平方式。

配方法是数学中一种重要的恒等变形的方法，它的应用十分非常广泛，在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。 

2、因式分解法。

因式分解，就是把一个多项式化成几个整式乘积的形式。

因式分解是恒等变形的基础，它作为数学的一个有力工具、一种数学方法在代数、几何、三角等的解题中起着重要的作用。

因式分解的方法有许多，除课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法等外，还有如利用拆项添项、求根分解、换元、待定系数等等。