要填充单位圆的内部，有多少不同的方法？

1、用圆工具，直接绘制单位圆：

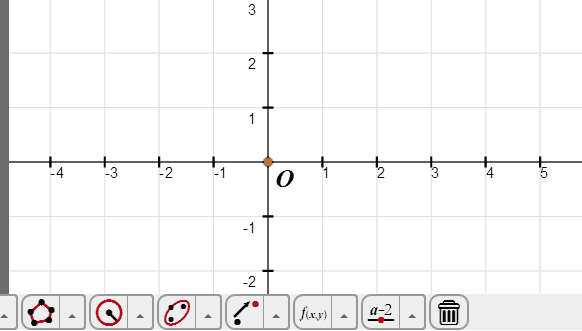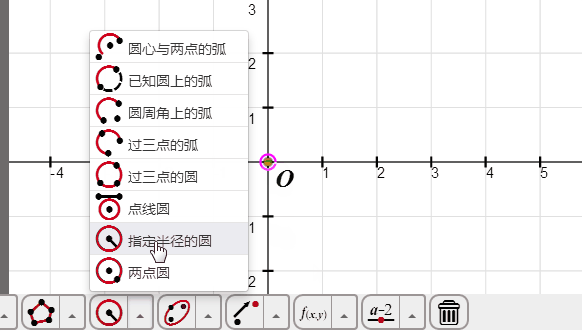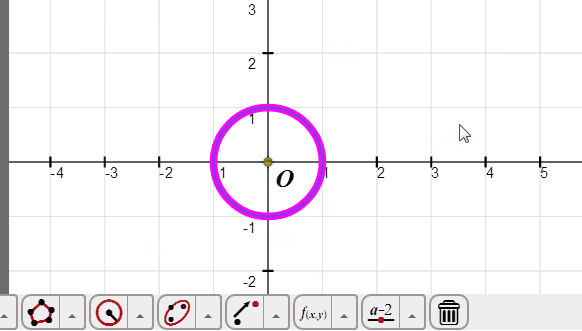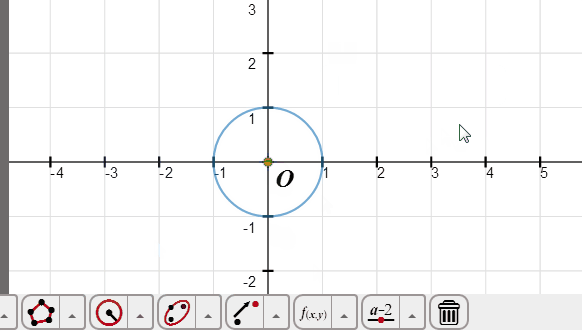
选择坐标原点O，再点击圆工具里面的“指定半径的圆”按钮，在弹出的对话框里面输入1，确定，单位圆就绘制完成了。

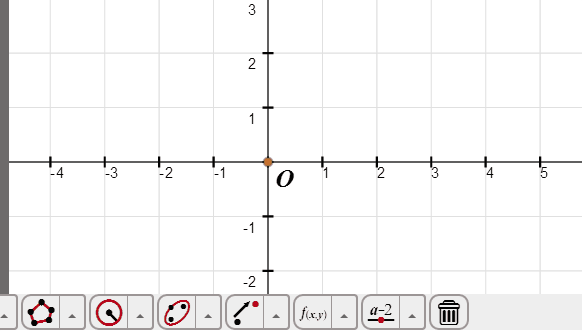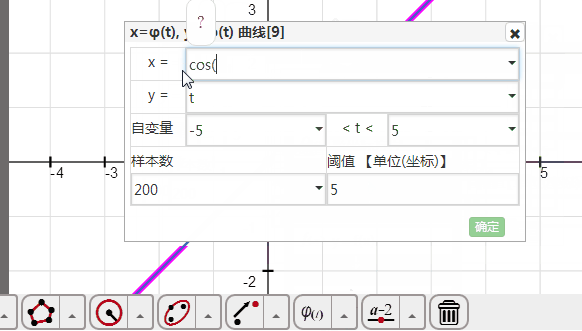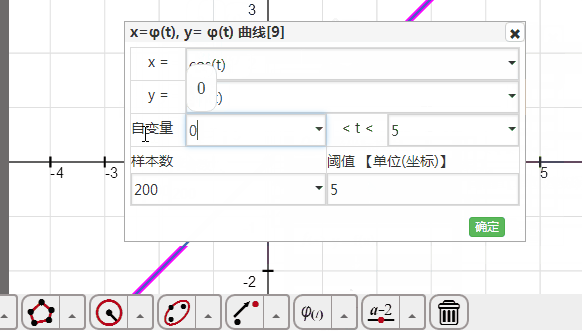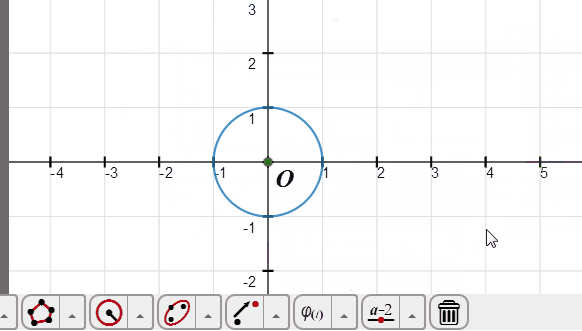
2、用参数方程绘制单位圆：

在函数工具里面找到“参数方程”按钮，点击一下，弹出参数方程对话框；

x后面输入cos(t)；

y后面输入sin(t)；

绘图区间改为0<t<2*pi，确定。

3、用极坐标方程绘制单位圆：

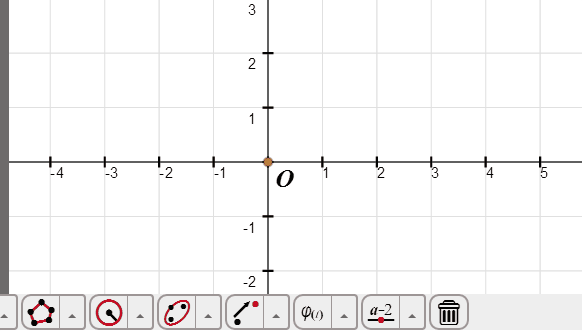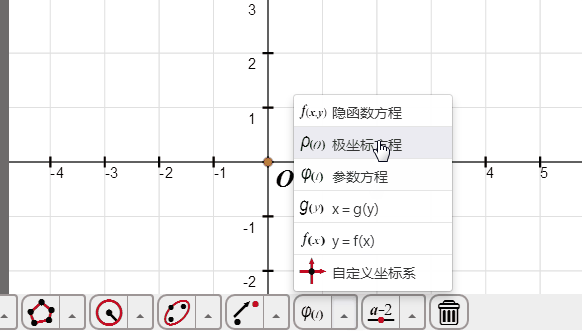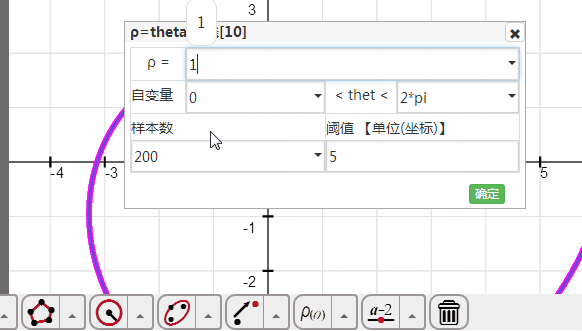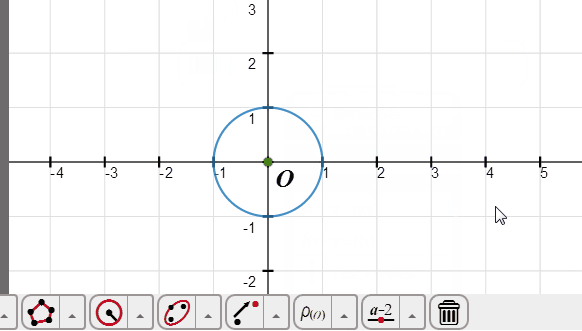
在函数工具里面找到“极坐标方程”按钮，点击一下，弹出极坐标方程对话框；

在ρ后面输入1；

参数范围是0<thet<2*pi；

确定。

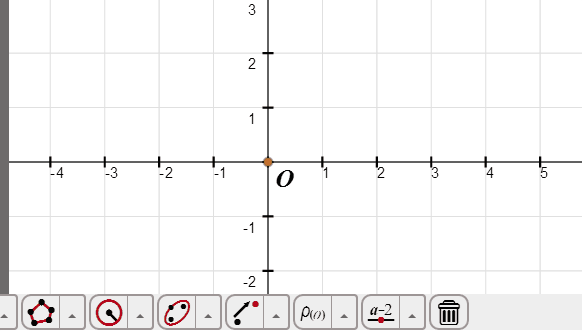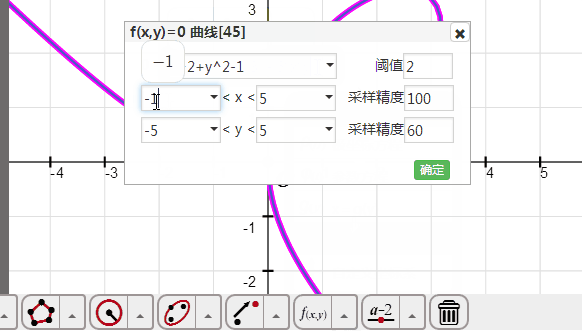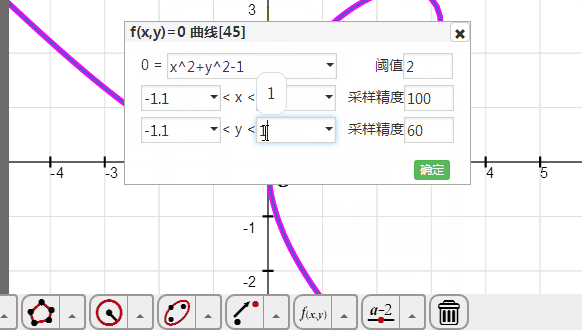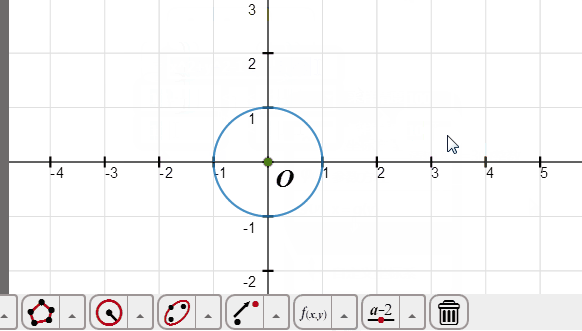
4、用隐函数方程绘制单位圆：

打开“隐函数方程”对话框，在0后面输入x^2+y^2-1；

绘图区间都改为-1.1到1.1；

采样精度都改为100；

确定。

1、直接填充：

选择单位圆，载使用右上角的着色工具着色。

2、绘制单位圆上的动点；

连接圆心与动点为线段；

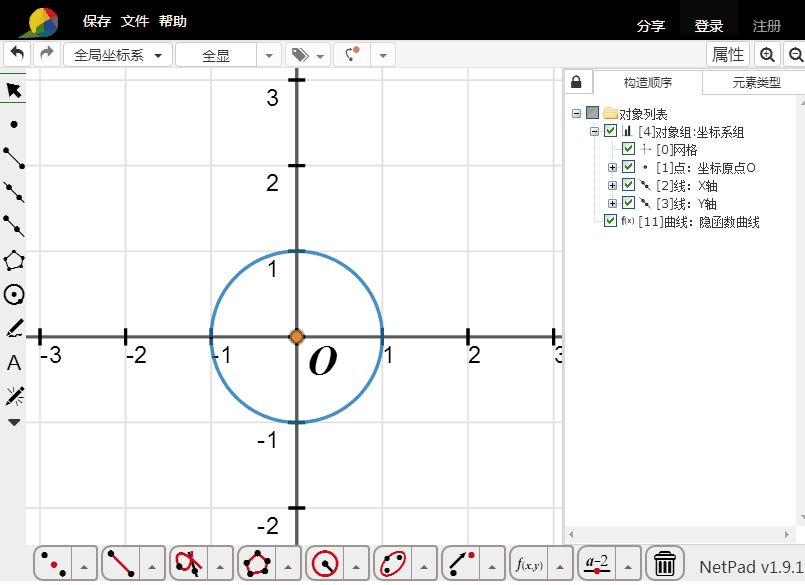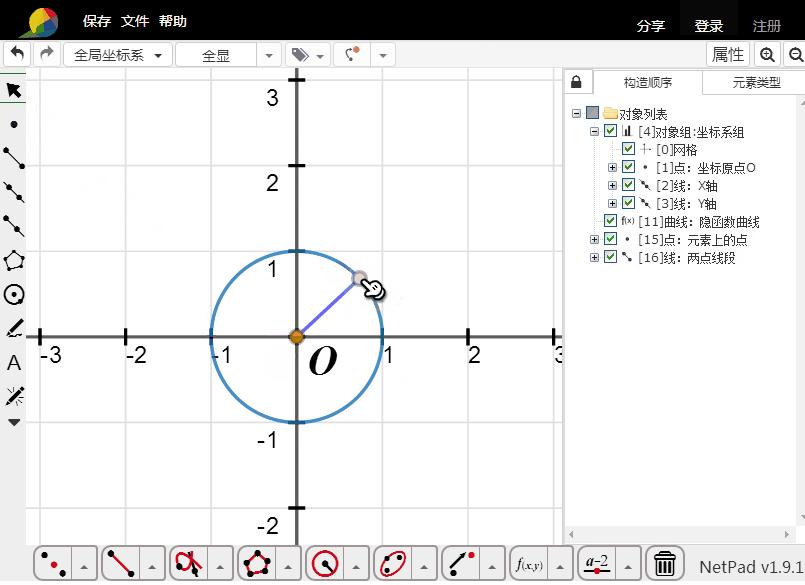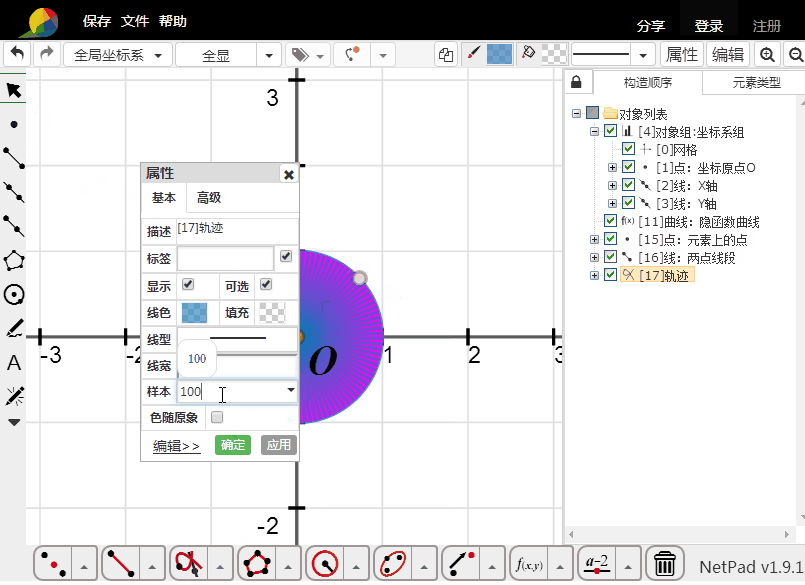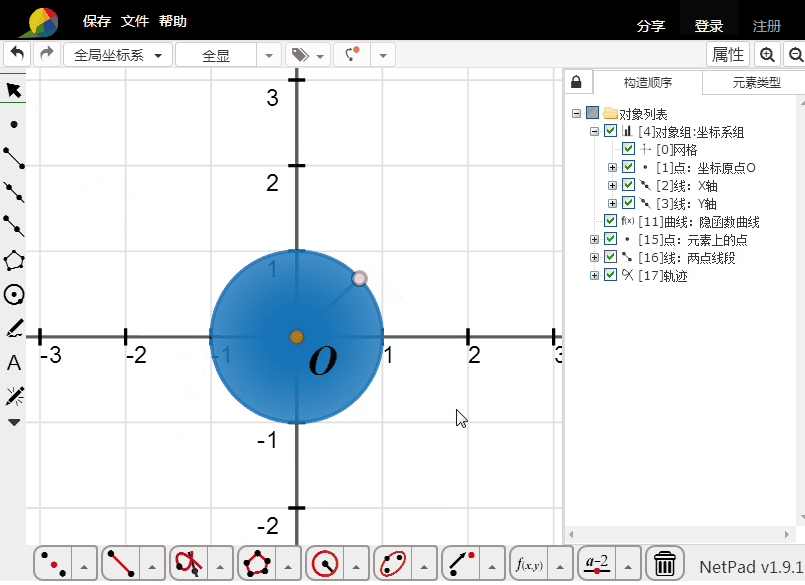
根据动点，构造线段的轨迹；

把轨迹的样本数改为300，确定。

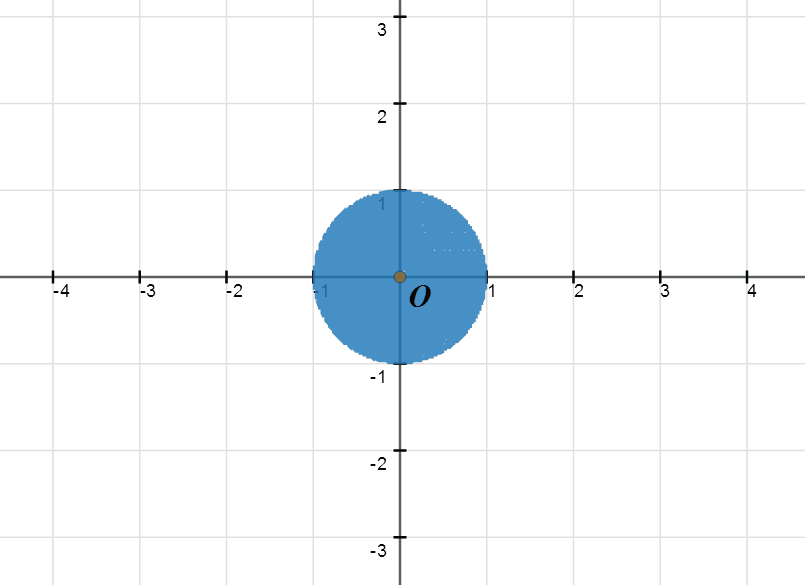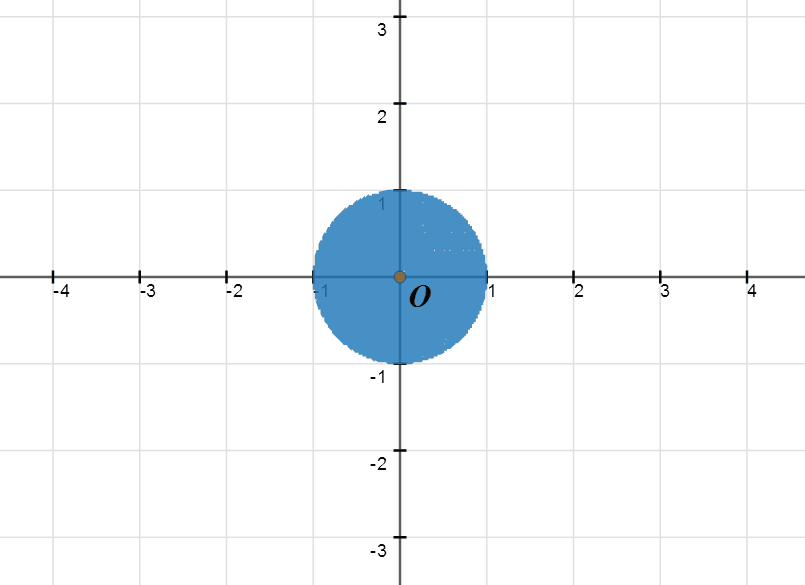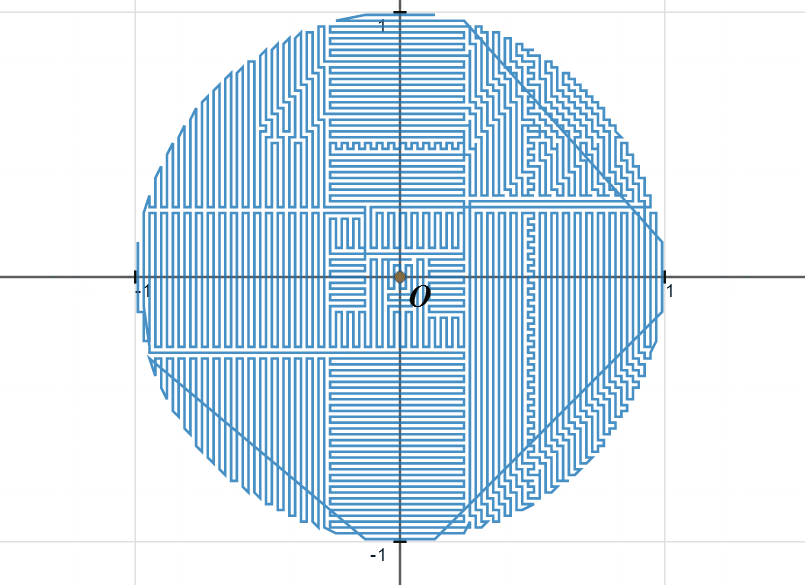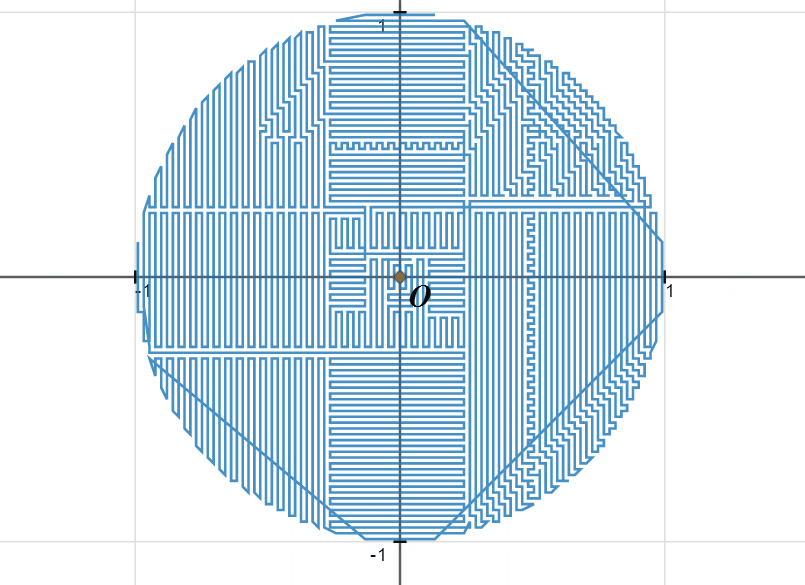
这个填充，其实是假象。

要想完全填充，样本数基本上得是无限大。

3、绘制半径为0.5的单位圆；

把线宽改为55，看起来就是填充了单位圆。

然而，只要稍微放大整个图像，就会发现露白了。

也就是说，这个填充也是假的。

4、用同心圆填充：

构造变量r，最小值0，最大值1；

计算r+1；

以原点为圆心，r为半径作圆；

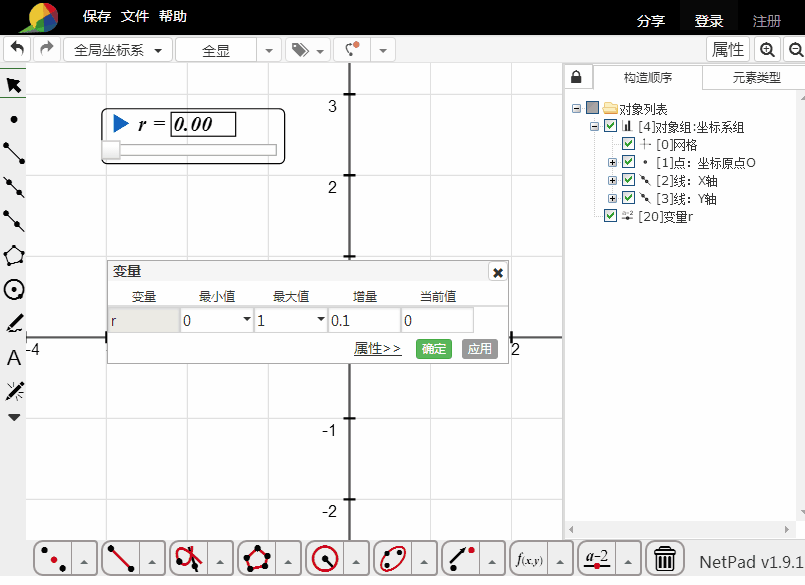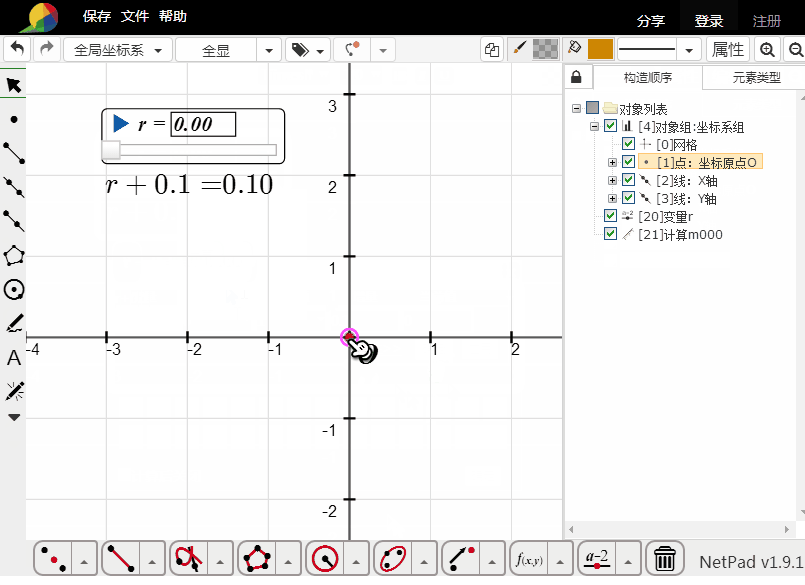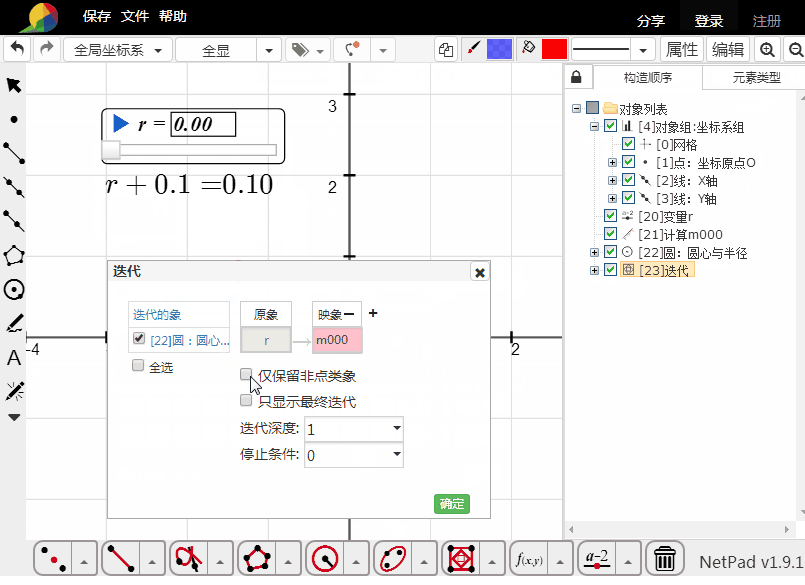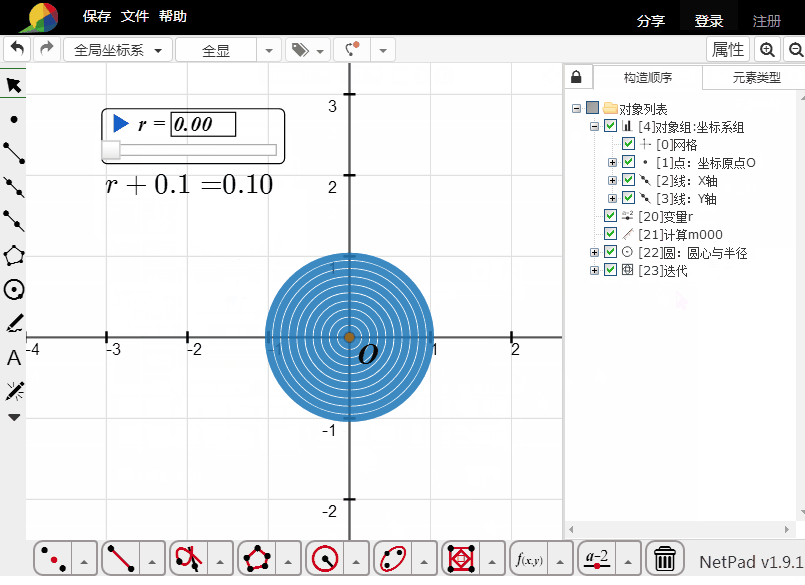
进行r到r+0.1的迭代变换，迭代深度是10；

加粗初始的圆的线宽。

这也是假填充。

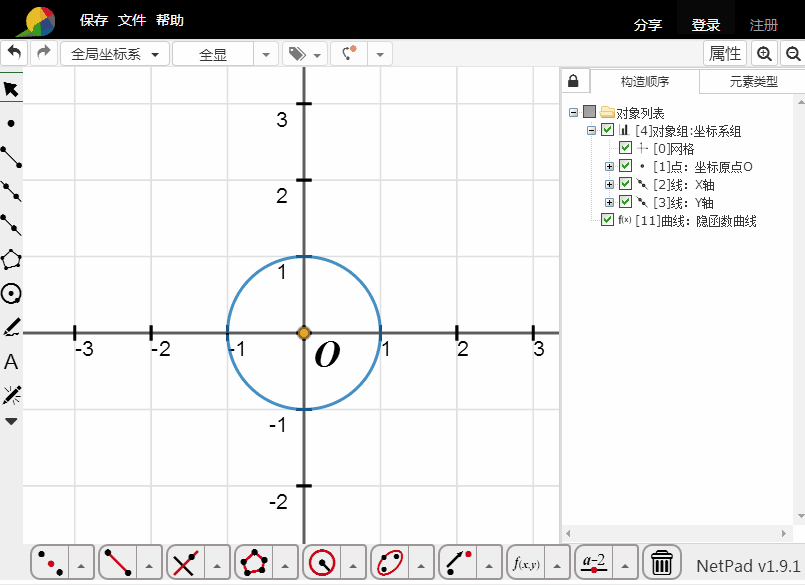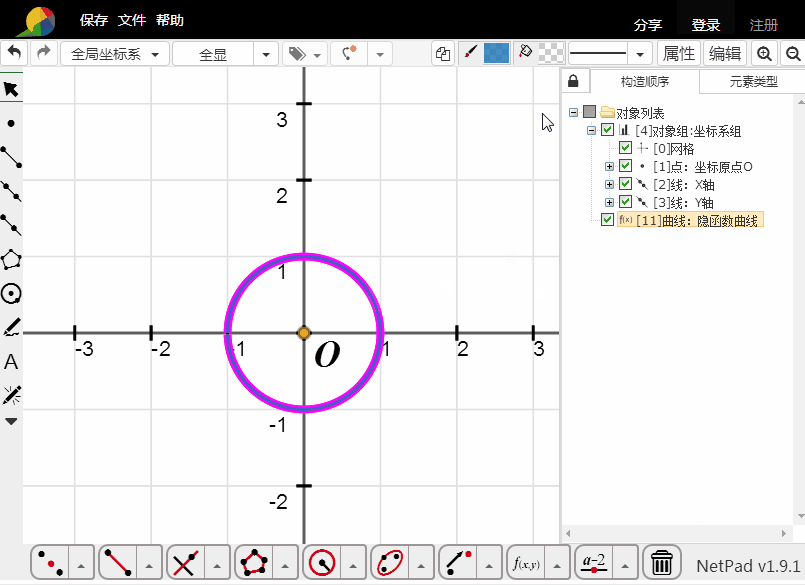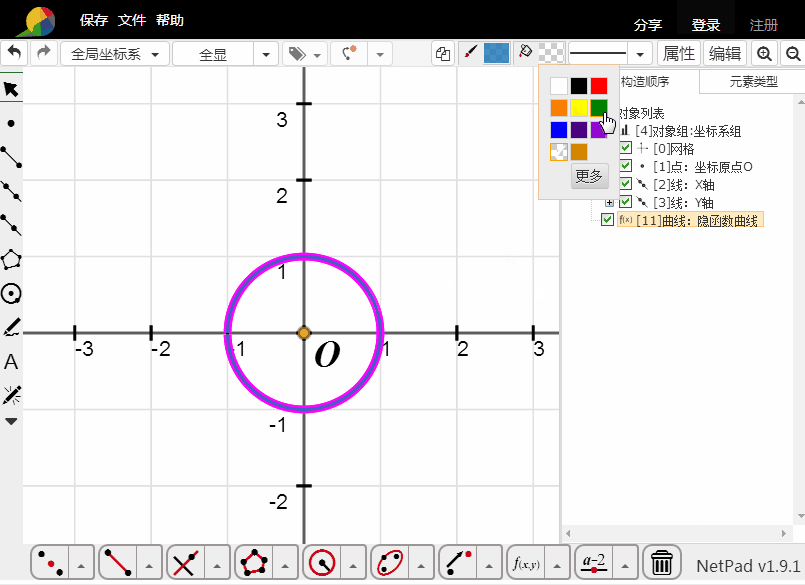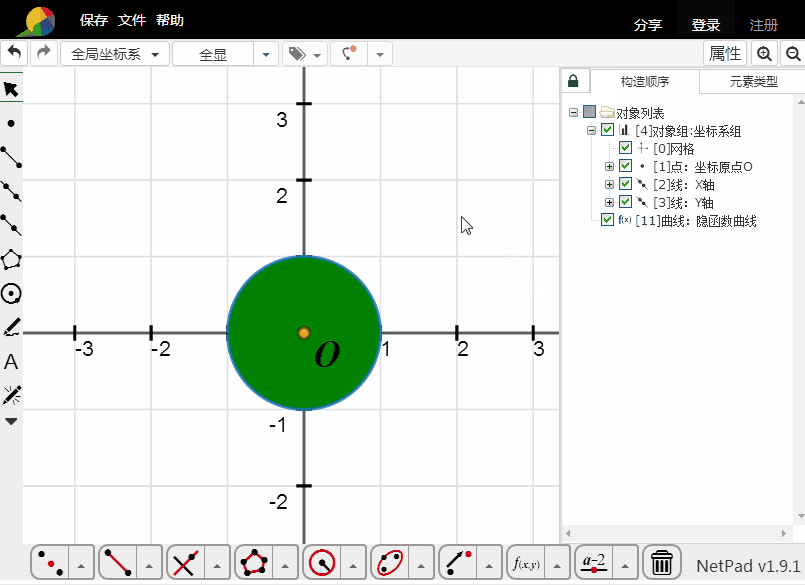
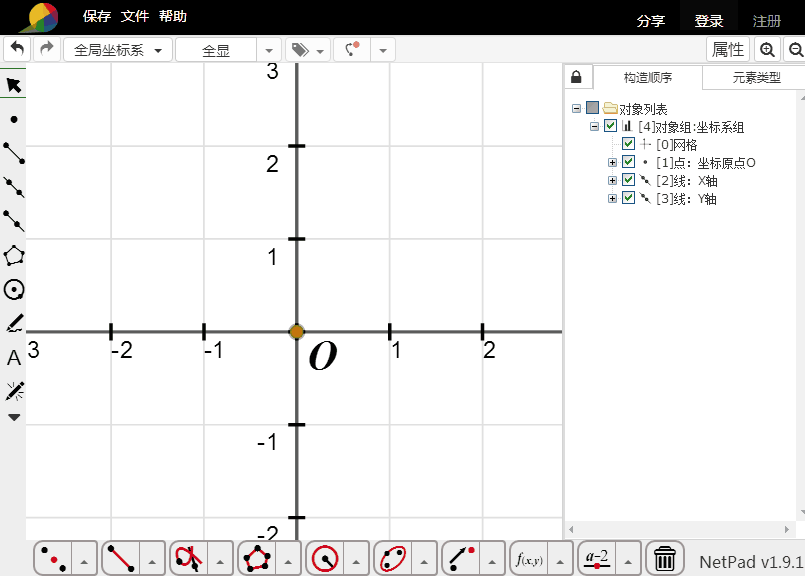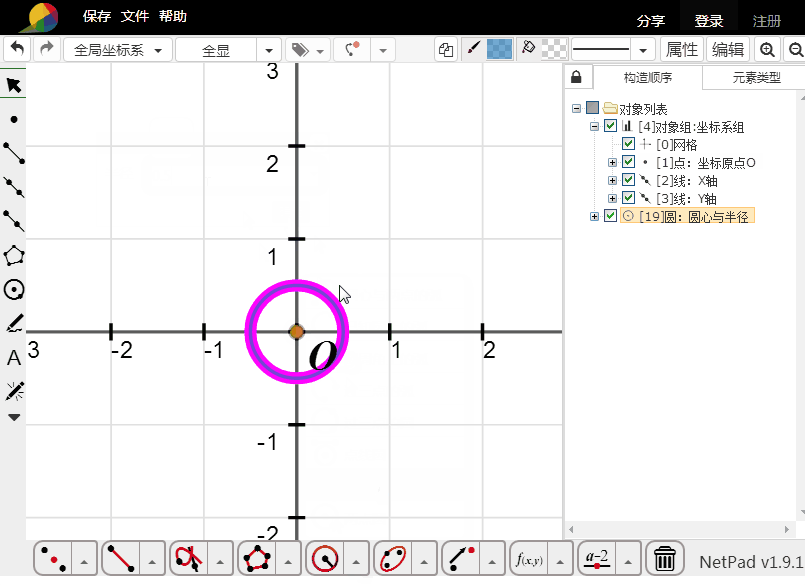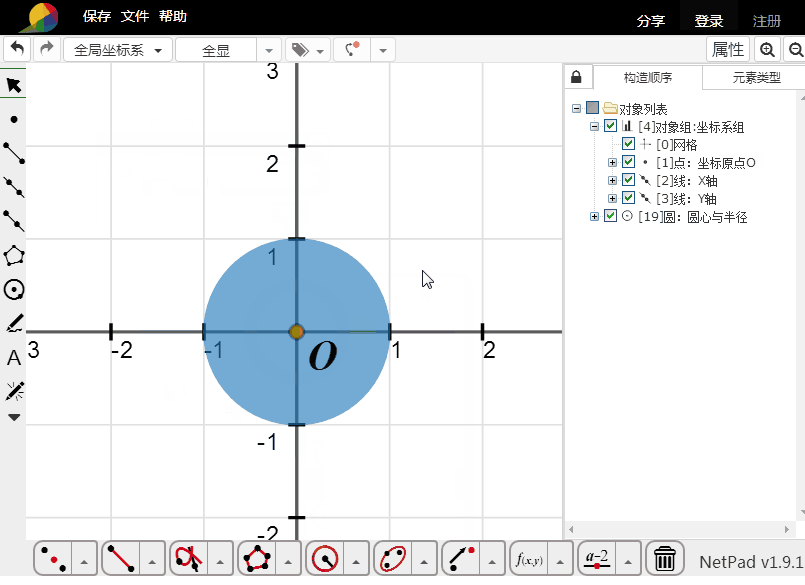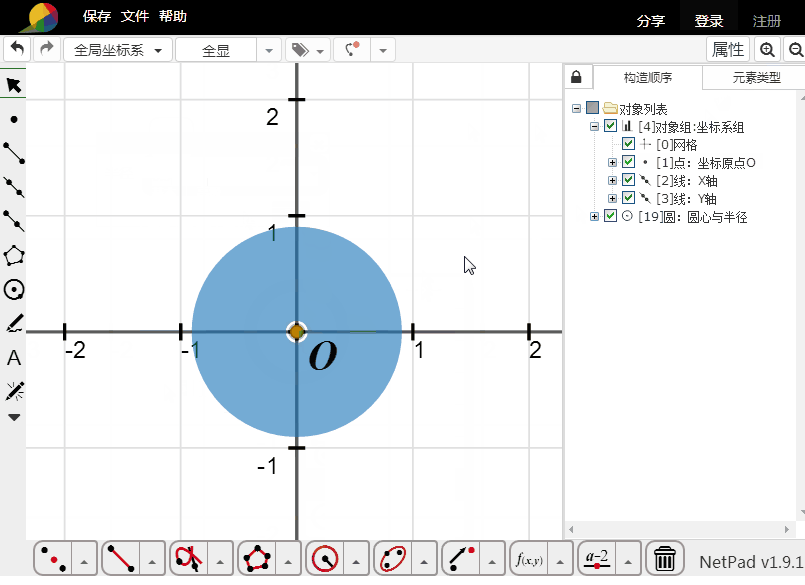
5、用隐函数方程填充：

x^2+y^2-1=0代表单位圆，那么——

abs(x^2+y^2-1)+x^2+y^2-1=0就代表单位圆及其内部所有点的集合。

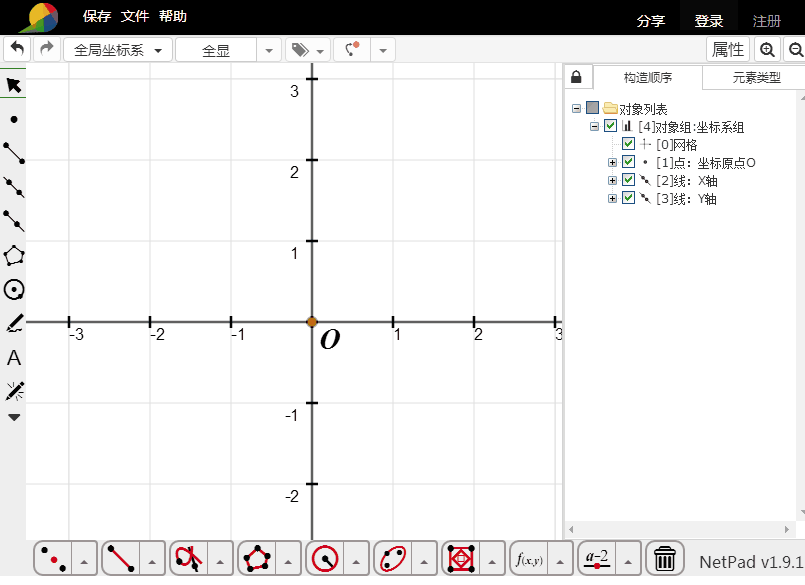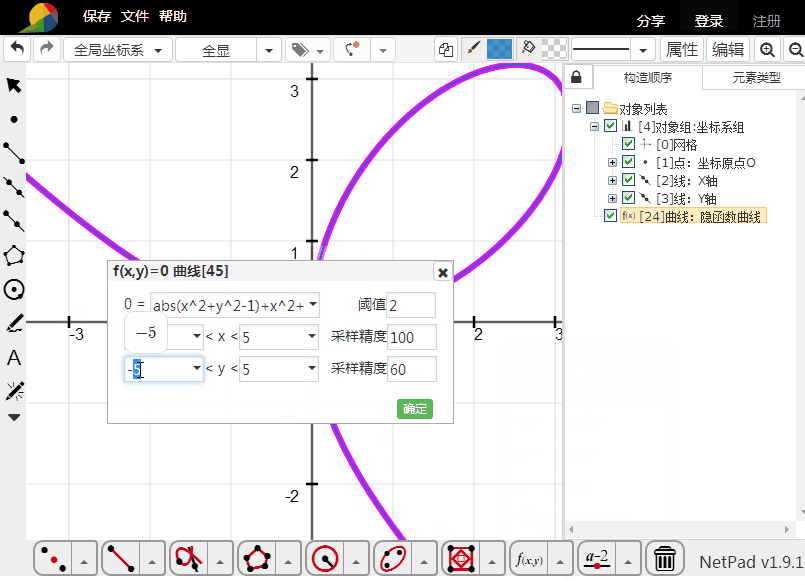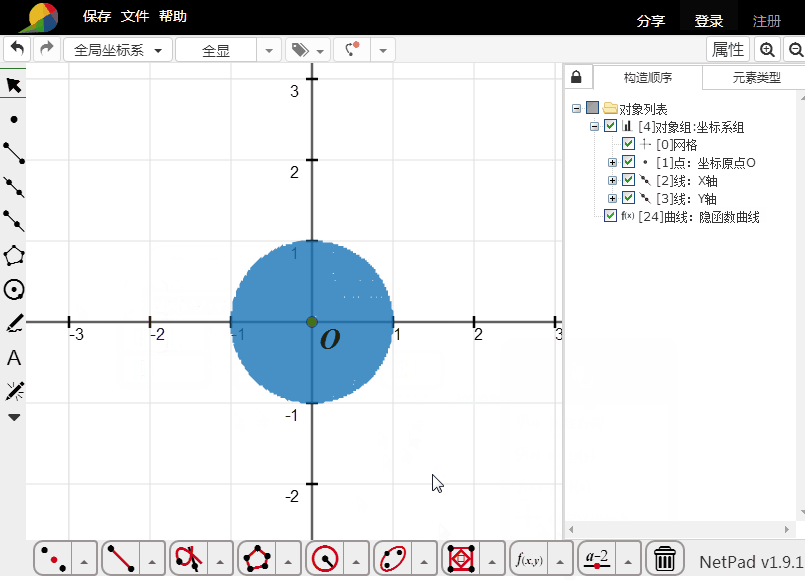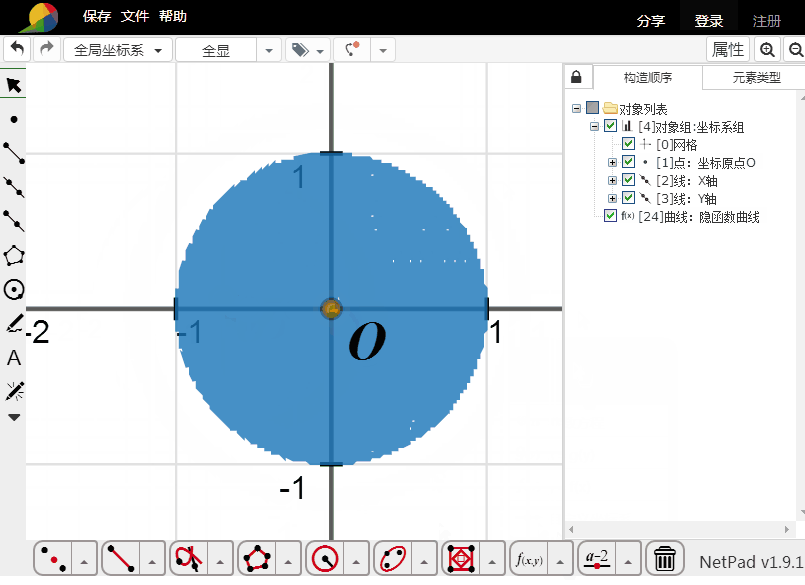
6、这个方法的填充，绝对是真正的填充，虽然看起来是假的。

这跟网络画板作图受制于样本数有关系。