曲线的切向量怎么求

1、假设曲线的参数方程是：

r = {Cos[2 t], Sin[3 t]};

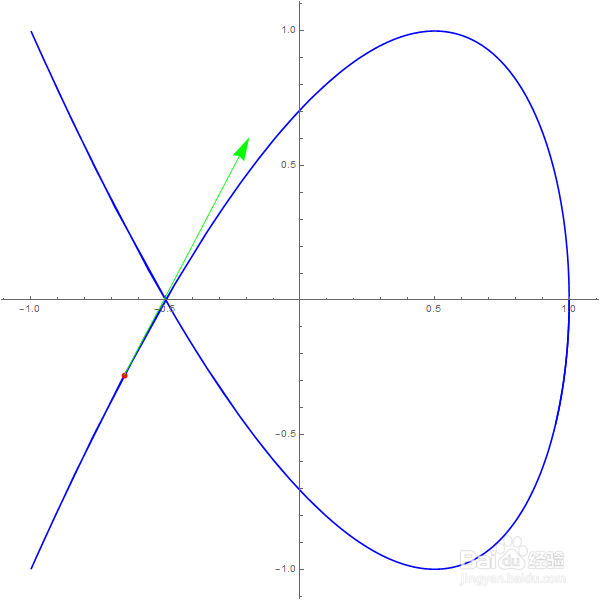
其图像如下。

2、曲线的切向量，可以统一描述为：

D[r, t]

3、当t=2的时候，作出曲线上这个点的位置：

Graphics[{Red, PointSize[0.01], Point[r /. t -> 2]}]

得到的就是下图的红色点的位置。

4、画出这个点的切向量。

这个点的切向量是：

D[r, t] /. t -> 2

5、切向量作图：

Graphics[{Green, Thickness[0.002], 

  Arrow[{r /. t -> 2, r + D[r, t] /. t -> 2}]}]

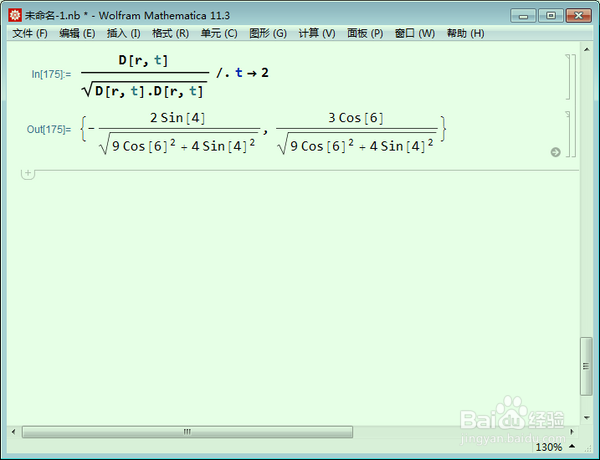
6、单位切向量是：

D[r, t]/Sqrt[D[r, t].D[r, t]] /. t -> 2