正多边形对称群的构造

1、正多边形对称群的元素，可以分为两大类：旋转、反射。

旋转有一个特例，那就是中心对称；

反射就是轴对称变换。

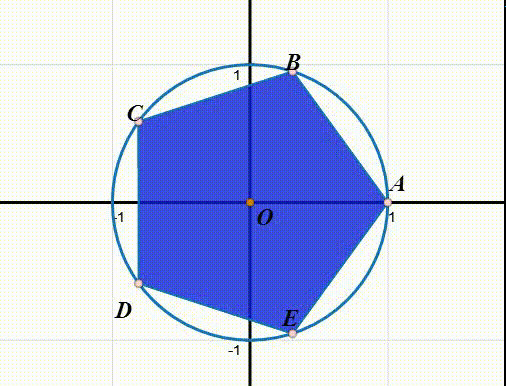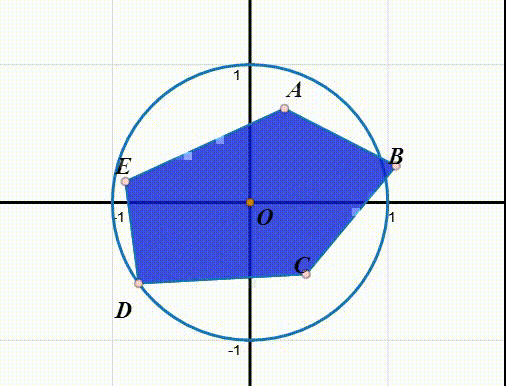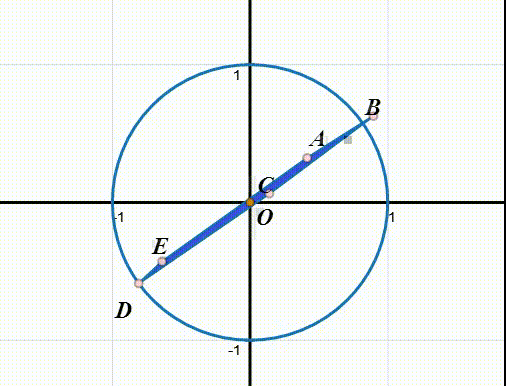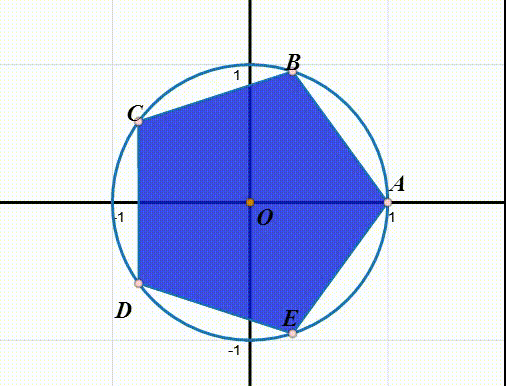
2、以正五边形对称群为例：

除了恒等变换，那么最小的旋转，就是绕中心旋转2π/5。

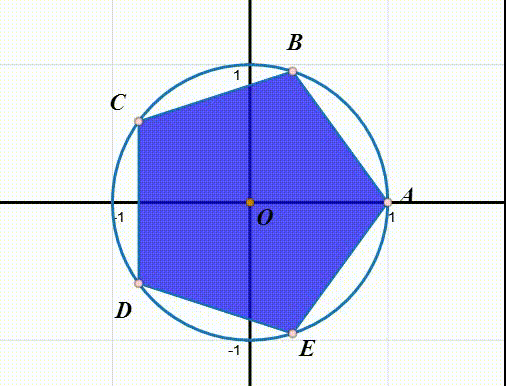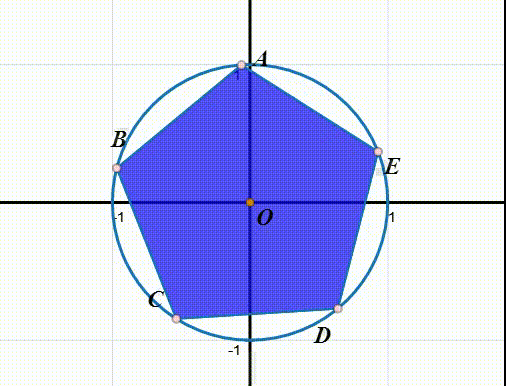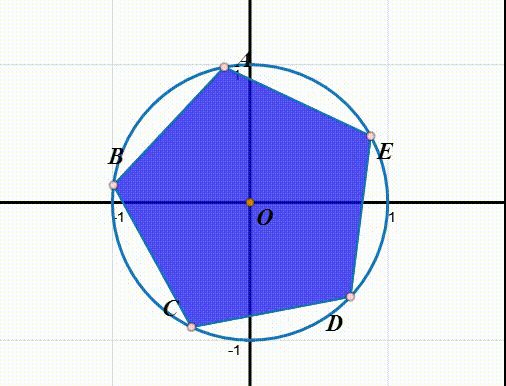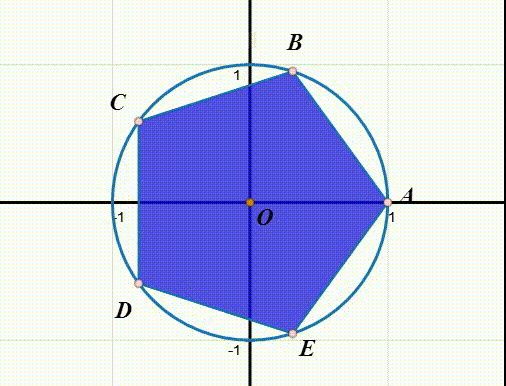
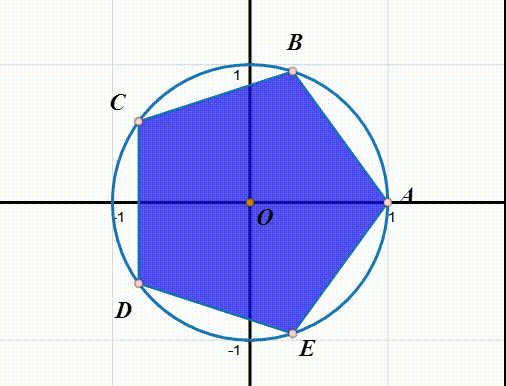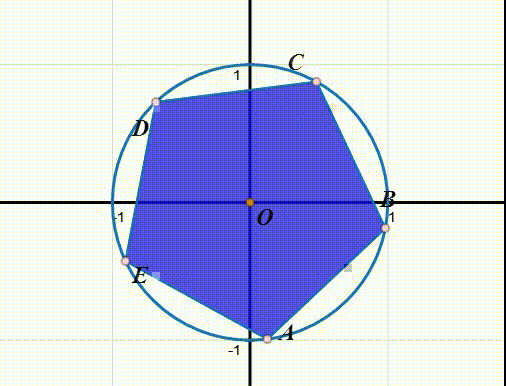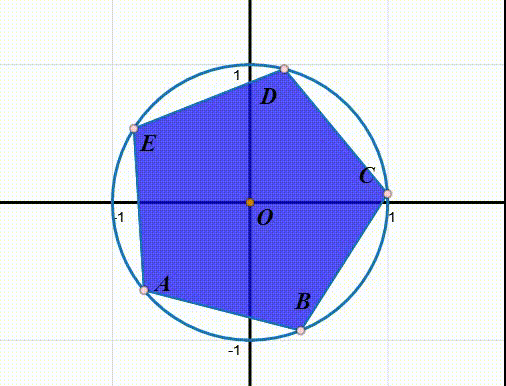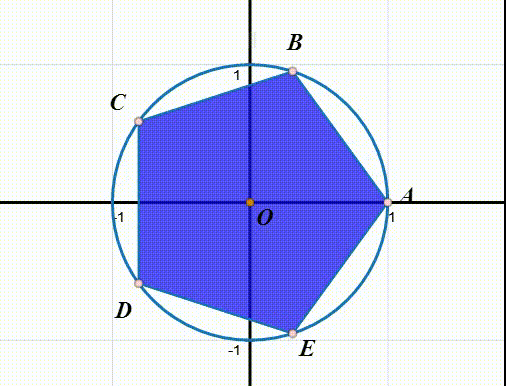
设r表示绕中心逆时针旋转2π/5，那么，给定正五边形ABCDE，有：

r(ABCDE)=EABCD

这个过程中，唯一的不动点就是中心点。

3、如果要逆时针旋转4π/5，就可以表示为：

r(r(ABCDE))=r(EABCD)=DEABC

或者写成：

r^2

4、实际上，r^5就表示恒等变换。

5、绕某一条对称轴进行反射，记为q：

q(ABCDE)=BAEDC

q^2就是恒等变换。