中考数学之函数的应用

1、【典例一】一次函数相关应用题

“年冬季越野赛”在滨河学校操场举行，某运动员从起点学校东门出发，途径湿地公园，沿比赛路线跑回终点学校东门．沿该运动员离开起点的路程（千米）与跑步时间（时间）之间的函数关系如图所示，其中从起点到湿地公园的平均速度是千米/分钟，用时分钟，根据图像提供的信息，解答下列问题：

（1）求图中的值；

（2）组委会在距离起点千米处设立一个拍摄点，该运动员从第一次过点到第二次过点所用的时间为分钟．

①求所在直线的函数解析式；

②该运动员跑完全程用时多少分钟？

2、【答案】

（1）10.5；

（2）①直线解析式为；②该运动员跑完赛程用时分钟．

1、【典例二】反比例函数相关应用题

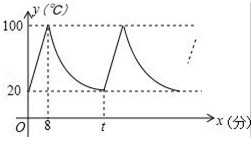
小明家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热[此过程中水温y（℃）与开机时间x（分）满足一次函数关系，当加热到100℃时自动停止加热，随后水温开始下降[此过程中水温y（℃）与开机时间x（分）成反比例关系，当水温降至20℃时，饮水机又自动开始加热…，重复上述程序（如图所示），根据图中提供的信息，解答下列问题：

（1）当0≤x≤8时，求水温y（℃）与开机时间x（分）的函数关系式；

（2）求图中t的值；

（3）若小明在通电开机后即外出散步，请你预测小明散步45分钟回到家时，饮水机内的温度约为多少℃？

2、【答案】

（1）y=10x+20；

（2）t=40；

（3）小明散步45分钟回到家时，饮水机内的温度约为70℃．

1、【3】二次函数相关应用题

某商场试销一种成本价为每件60元的服装，规定试销期间销售单价不低于成本单价，获利不得高于40%．经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=80时，y=40；x=70时，y=50．

（1）求一次函数y=kx+b的表达式；

（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？

2、【答案】

（1）一次函数的解析式为y=﹣x+120（60≤x≤84）；

（2）销售价定为每件84元时，可获得最大利润，最大利润是864元．

【解析】

（1）根据题意得：销售单价x≥成本60元，获利不得高于40%，则销售单价x≤60（1+40%）；再利用待定系数法把x=80时，y=40；x=70时，y=50代入一次函数y=kx+b中，求出k，b即可得到关系式；

（2）根据题目意思，表示出销售额和成本，然后表示出利润=销售额-成本，整理后根据x的取值范围求出最大利润．

（1）60≤x≤60（1+40%），

∴60≤x≤84，

解得：k=﹣1，b=120，

∴一次函数的解析式为y=﹣x+120（60≤x≤84）；

（2）销售额：xy=x（﹣x+120）元；成本：60y=60（﹣x+120），

∴W=xy﹣60y，

=x（﹣x+120）﹣60（﹣x+120），

=（x﹣60）（﹣x+120），

=﹣x2+180x﹣7200，

=﹣（x﹣90）2+900，

∴W=﹣（x﹣90）2+900，（60≤x≤84），

当x=84时，W取得最大值，最大值是：﹣（84﹣90）2+900=864（元），

即销售价定为每件84元时，可获得最大利润，最大利润是864元．