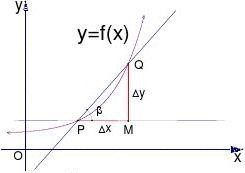
三次函数y=x^3-5x的图像及单调和凸凹等性质

1、       通过函数的定义域、单调性、凸凹性、极限和奇偶性等性质，介绍函数用导数工具画函数y=x^3-25x的图像的主要步骤。

1、观察函数特征，函数为自变量的多项式和，即函数y=x^3-25x自变量x可以取全体实数，即定义域为：(-∞，+∞）。

2、计算求出函数y=x^3-25x的一阶导数，结合函数的定义域求出函数驻点，由一阶导数的正负，判断函数的单调性，并计算出函数的单调区间。

y=x^3-25x

y'=3x^2-25.

令y'=0,则x^2=25/3，即x=±5√3/3，即为驻点的横坐标。

3、如果函数f(x)在区间I上二阶可导，则f(x)在区间I上是凸函数的充要条件是f''(x)<=0。

y=x^3-25x

dy/dx=3x^2-25,

d^2y/dx^2=6x,即y''=6x,则拐点的横坐标x=0.

4、函数的极限，即求出函数在无穷处的极限。

函数在负无穷处取负无穷大，正无穷大处取正无穷大。

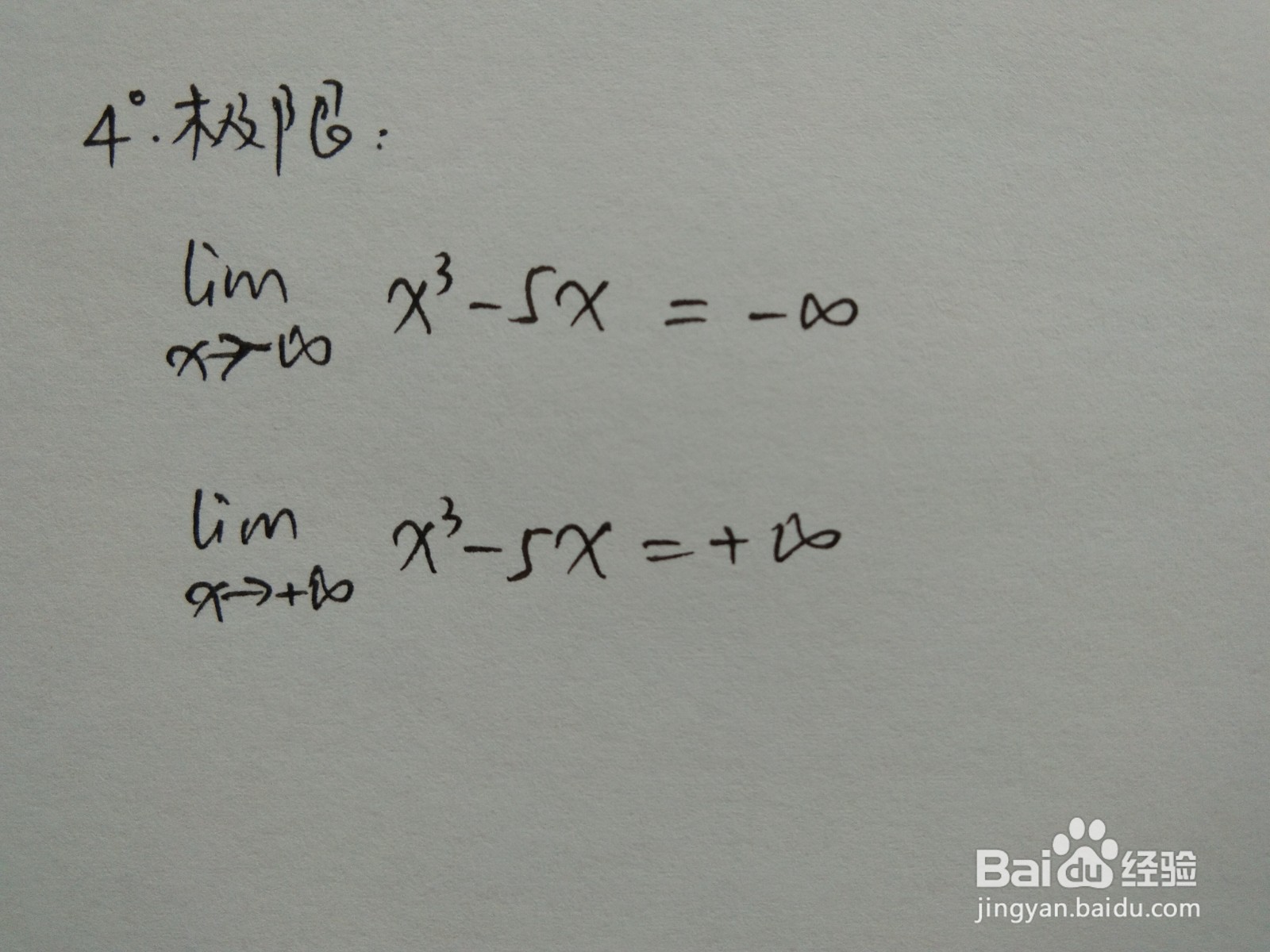
5、根据函数的奇偶性的判断方法，对于本题由于f(-x)=-f(x),所以函数为奇函数，函数图像关于原点对称，主要判断过程如下图所示：

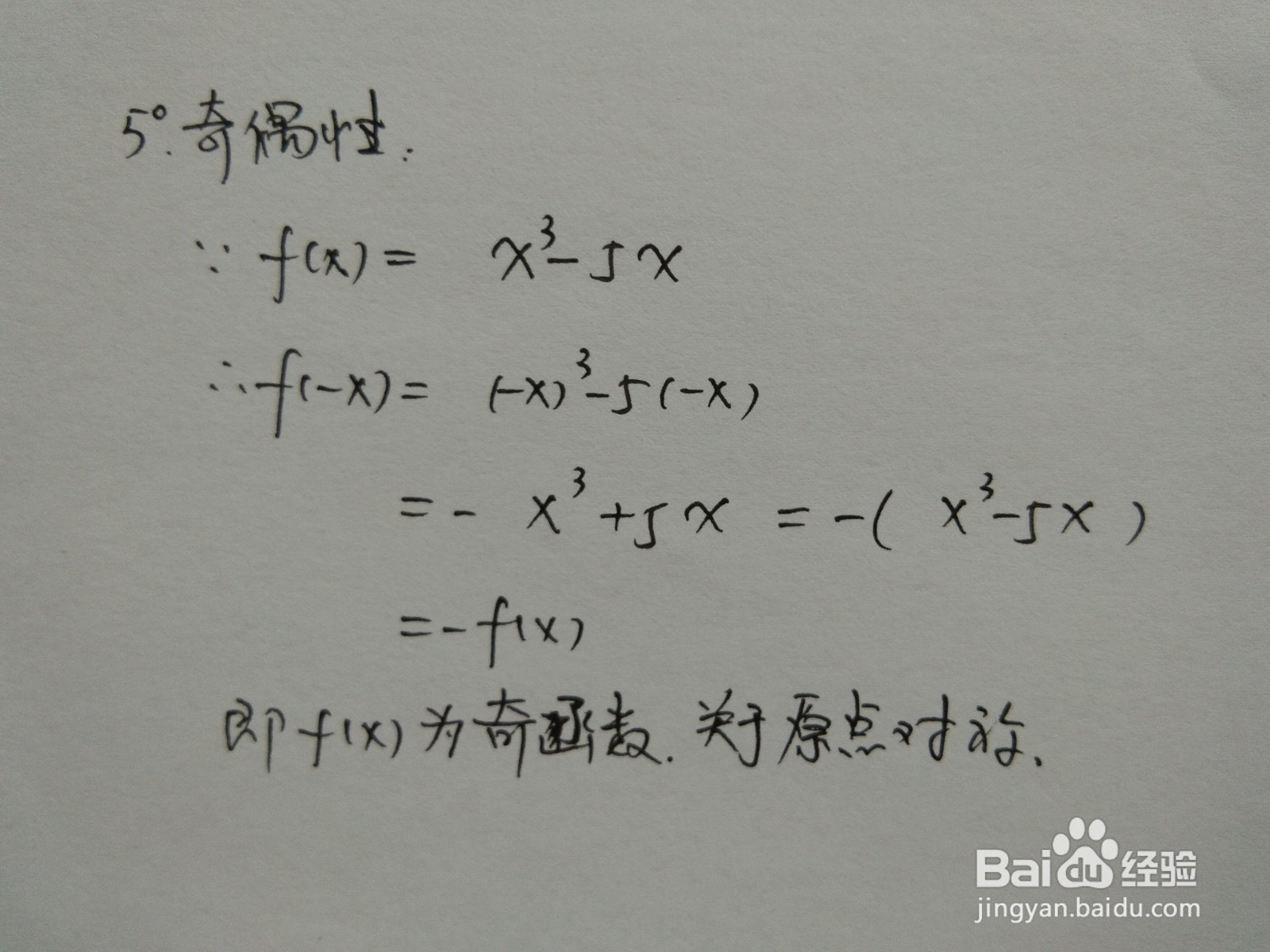
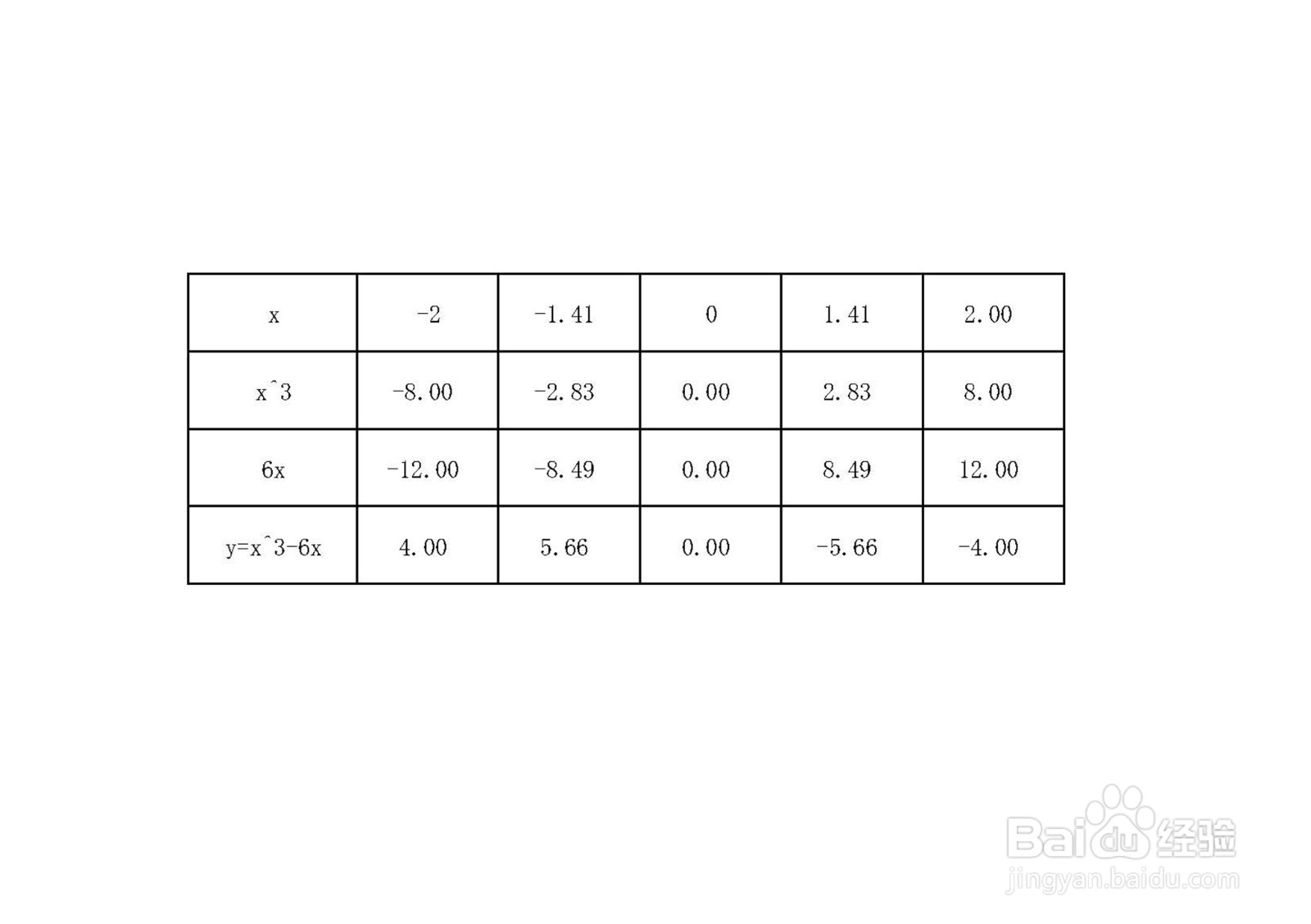
6、本题三次奇函数图像上部分点，列出五点示意图解析函数上的五点图如下表所示。

例如当x=0时，y=0，

当x=-1时，y=（-1）^3-25*（-1）=-3+25=22；

当x=1时，y=1^3-25*1=1-25=-24.

即经过点(0，0),(1，-24),(-1，22).

7、根据以上函数的定义域、单调性、凸凹性、奇偶性以及极限等相关性质，并在函数的定义域前提下，即可简要画出函数的图像，且该图像关于原点对称。

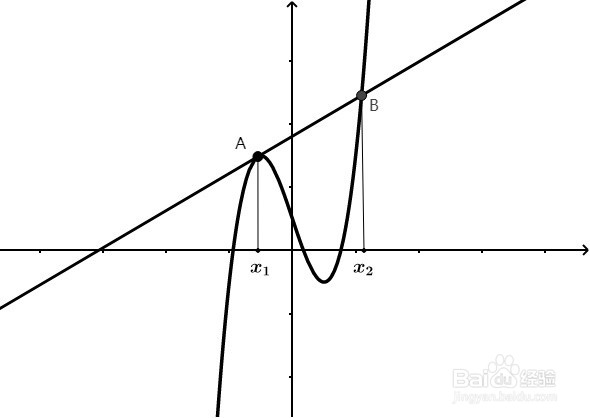
1、已知函数y=x3-5x，求:(1)求函数f(x)在点A(0,f(0))处的切线；(2)求函数f(x)单调区间及极值。

2、解：

当x=0时，y(1)=0-5*0=0;

y=1-5x,求导得：

y´=2x2-5,当x=0时，

y´(1)=2*02-5=-5，即为切线的斜率。

则切线的方程为:

y-0=-5(x-0),化为一般方程为：

y+5x=0。

3、y´=2x2-5，令y´=0，则x=±√5/2 .

1).当x∈(-∞，-√5/2 )和(√5/2 ，+∞)时，

y´>0,此时函数y为单调增函数，所求区间为单调增区间。

2).当x∈[-√5/2 ,√5/2 ]时，

y´<0,此时函数y为单调减函数，所求区间为单调减区间。

则在x1=-√5/2 处取极大值，在x2=√5/2处取极小值。

所以：

极大值=f(-√5/2 )

=-(√5/2 )3-5*(-√5/2 )=5√10/4;

极小值=f(52 )

=(√5/2 )3-5*(√5/2)=-5√10/4。