用Mathematica处理多点调控曲面

1、先来画一个简单的三点调控曲面（三个点都是正调控点）：

TraditionalForm[

 1/Sqrt[Abs[-1 + x]^2 + Abs[-2 + y]^2 + Abs[-3 + z]^2] + 

   1/Sqrt[Abs[x]^2 + Abs[-1 + y]^2 + Abs[-2 + z]^2] + 

   1/Sqrt[Abs[-1 + x]^2 + Abs[y]^2 + Abs[-2 + z]^2] == 2.6]

运行之后，再来：

ContourPlot3D[Evaluate[%], {x, -3, 3}, {y, -2, 4}, {z, 0, 6}, 

 Axes -> False, Boxed -> False, ContourStyle -> {Opacity[0.5], Blue}]

2、当等式右面的数值变小的话，如，取值1.5，图形变的稍微“丰满了”：

ContourPlot3D[

 1/Sqrt[Abs[-1 + x]^2 + Abs[-2 + y]^2 + Abs[-3 + z]^2] + 

   1/Sqrt[Abs[x]^2 + Abs[-1 + y]^2 + Abs[-2 + z]^2] + 

   1/Sqrt[Abs[-1 + x]^2 + Abs[y]^2 + Abs[-2 + z]^2] == 1.5

3、当右面数值变大，图形就会越来越“消瘦”：

ContourPlot3D[

 1/Sqrt[Abs[-1 + x]^2 + Abs[-2 + y]^2 + Abs[-3 + z]^2] + 

   1/Sqrt[Abs[x]^2 + Abs[-1 + y]^2 + Abs[-2 + z]^2] + 

   1/Sqrt[Abs[-1 + x]^2 + Abs[y]^2 + Abs[-2 + z]^2] == 2.85

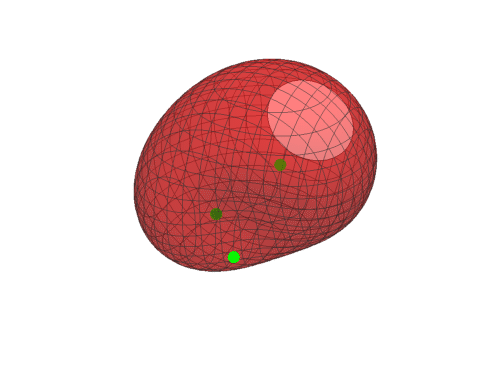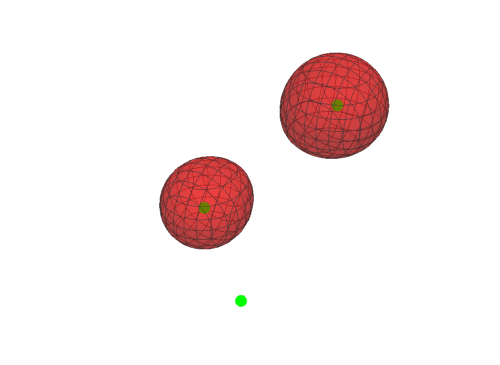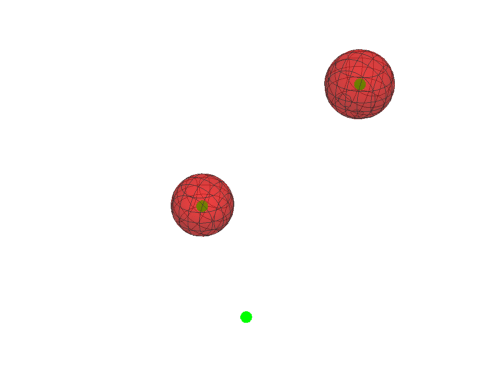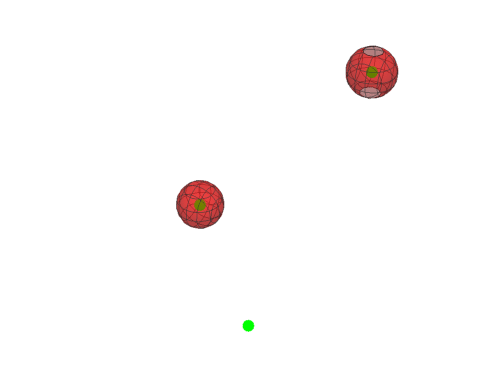
4、用互动效果演示一番上面的变化过程，同时把三个调控点也画出来：

Manipulate[

 Show[Graphics3D[{PointSize[0.036], Green, 

    Point[{{1, 2, 3}, {0, 1, 2}, {1, 0, 2}}]}], 

  ContourPlot3D[………… == a, {x, -3, 

    3}, {y, -2, 4}, {z, 0, 6}, ContourStyle -> {Opacity[0.5], Red}], 

  Boxed -> False], {a, 1.5, 10}]

5、上述过程导出GIF图片：

Export["C:\\Users\\Administrator\\Desktop\\0.gif",……]

6、如果把其中一个点定为负调控点，这个点就会被“排斥”在曲面之外：

1/Sqrt[Abs[-1 + x]^2 + Abs[-2 + y]^2 + Abs[-3 + z]^2] + 1/Sqrt[

   Abs[x]^2 + Abs[-1 + y]^2 + Abs[-2 + z]^2] - 1/Sqrt[

   Abs[-1 + x]^2 + Abs[y]^2 + Abs[-2 + z]^2] == a // TraditionalForm

同样是运行之后，再来：

Manipulate[

 Show[Graphics3D[{PointSize[0.036], Green, 

    Point[{{1, 2, 3}, {0, 1, 2}, {1, 0, 2}}]}], 

  ContourPlot3D[Evaluate[%], {x, -3, 3}, {y, -2, 4}, {z, 0, 6}, 

   ContourStyle -> {Opacity[0.5], Red}], Boxed -> False], {a, 0.5, 5}]