Plot图形的时候,碰到自变量是复数,该怎么办?
1、自定义惹迅函数:
复数图[f_, {xmin_, xmax_}, {ymin_, ymax_}, 选项:OptionsPattern[]] := RegionPlot[True, {x, xmin, xmax}, {y, ymin, ymax},选项, PlotPoints -> 100, ColorFunctionScaling -> False, ColorFunction -> Function[{x, y}, With[{ff = f[x + I y]}, Hue[(2. Pi)^-1 Mod[Arg[ff], 2 Pi], 1, 1 - (1.2 + 10 Log[Abs[ff] + 1])^-1]]]]
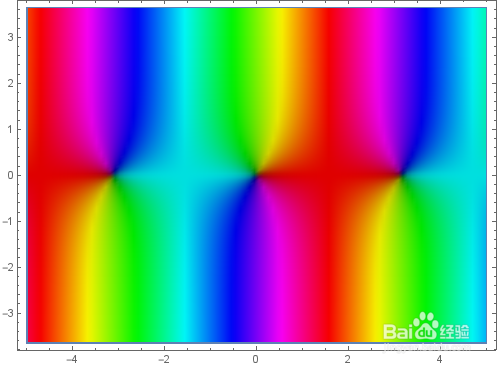
作正弦函数的复数图:
复数图[Sin, {-5, 5}, {-3.65, 3.65},AspectRatio->Automatic]
注伐彩意,这个图里面没有图线,完全是靠颜色来表现整个图形。
2、注意,ColorFunctionScaling -> False是必不可少的,取消渐变色,廊付爬防止整个图形的颜色过于笼统。
复数图0[f_, {xmin_,xmax_},{ymin_,ymax_},选项:OptionsPattern[]]:= RegionPlot[True, {x,xmin,xmax},{y, ymin, ymax},选项, PlotPoints ->100,ColorFunction ->Function[{x, y},With[{ff=f[x+I y]}, Hue[(2. Pi)^-1 Mod[Arg[ff],2 Pi],1,1 -(1.2 +10 Log[Abs[ff]+1])^-1]]]]

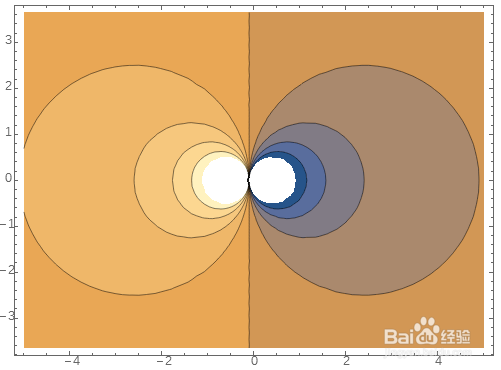
1、给出复数方程:
f[t_]:= (25 t)/(1 + 10 t);
当t为复数x+I y的时候,那么实部和虚部对应的等高线图如下:
ContourPlot[Re@f[x+I y],{x,-5, 5}, {y,-3.65, 3.65}]

2、f[t_]:= (25 t)/(1 + 10 t);
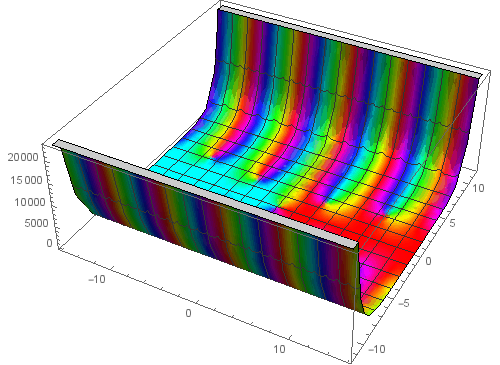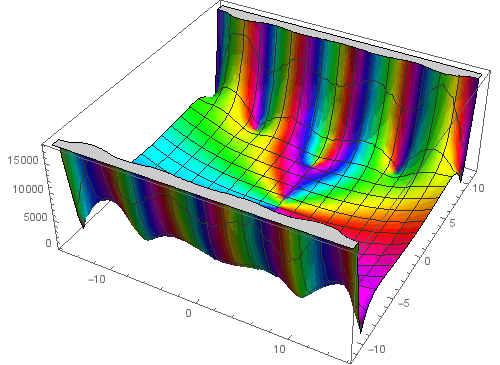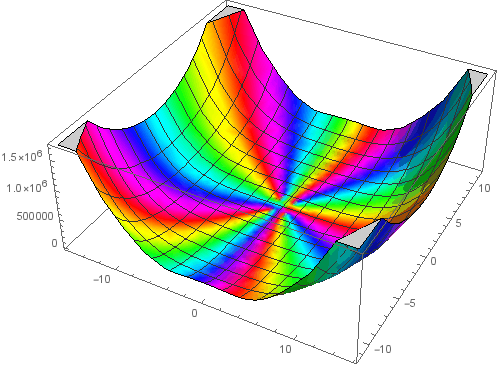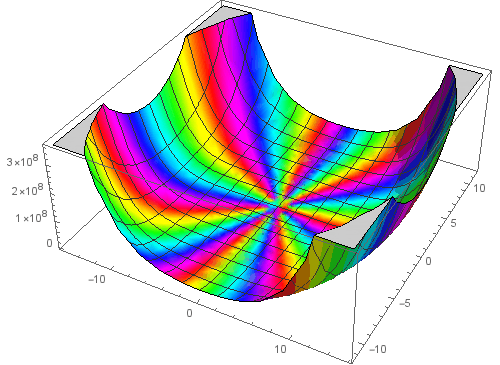
把实部和虚部、y/10作为曲面的参数方程,绘制这个曲面。
ParametricPlot3D[{Re[f[x+I y]],Im[f[x+I y]],y/10},{x,-10,10},{y,-3.65,3.65}]
把实部和虚部、1/(10 y)作为曲面的参数方程,绘制这个曲面。
ParametricPlot3D[{Re[f[x+I y]],Im[f[x+I y]],1/(10 y)},{x,-10,10},{y,-10,10}]


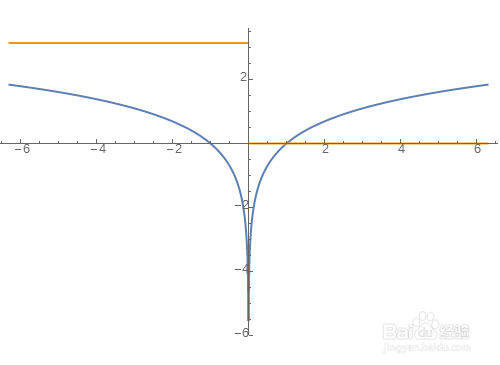
1、Plot[{Re@Log[x],Im@Log[x]}, {x, -2 Pi, 2 Pi},PlotStyle -> Thick,
PlotRange -> All]
把Log[x]视为单变量函数,分别作出实部和虚部对应的图像。
2、如果把Log[x]的实部和虚部,视为某条曲线的参数方程,试画出这条曲线。
ParametricPlot[{Re@Log[x],Im@Log[x]}, {x, -0.5,0.5}, PlotRange -> All]

1、立体复数图[f_, range_, 选项___] := Block[{p, q,g}, g[r_,i_]:=(f/.range[[1]]:>r+I i); Plot3D[Abs[g[p,q]], {p, Re[range[[2]]], Re[range[[3]]]}, {q, Im[range[[2]]], Im[range[[3]]]},选项, ColorFunction->(Hue[Mod[Arg[g[#1,#2]]/(2*Pi) + 1, 1]]&), ColorFunctionScaling->False]]
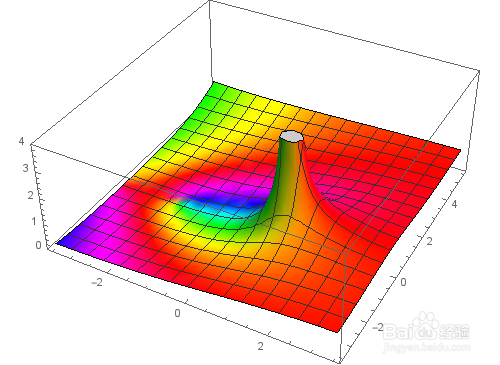
这个代码跟案例一,感觉差不多。作出Zeta函数的立体图形:
立体复数图[Zeta[z],{z,-3.5-3.5I,3.5+5.5I},PlotRange->{0,4}]
2、Gamma函数的立体图:
立体复数图[Gamma[z],{z,-5-3.65I,5+3.65I}]
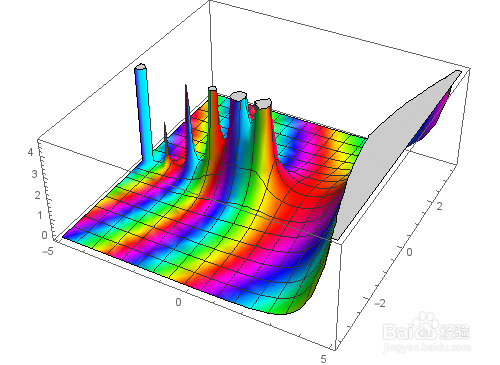
3、Sin[z]的图形:
立体复数图[Sin[z],{z,-5 Pi-3.65 I Pi,5 Pi+3.65 I Pi}]

4、Sin[z]+z^n,当n从1增到7,看看立体复数图有什么变化:
Export["000fushutu.gif",Table[立体复数图[Sin[z]+z^n,{z,-5 Pi-3.65I Pi,5 Pi+3.65I Pi},ImageSize->{500,365}],{n,1,7,1/6}],"AnimationRepetitions"->Infinity,"DisplayDurations"->1]