AVL树使用c++语言实现插入操作
1、【定义】AVL树指的是任一节点的左子树与右子树的高度差不超过1。下面两幅图展示AVL树的实例。
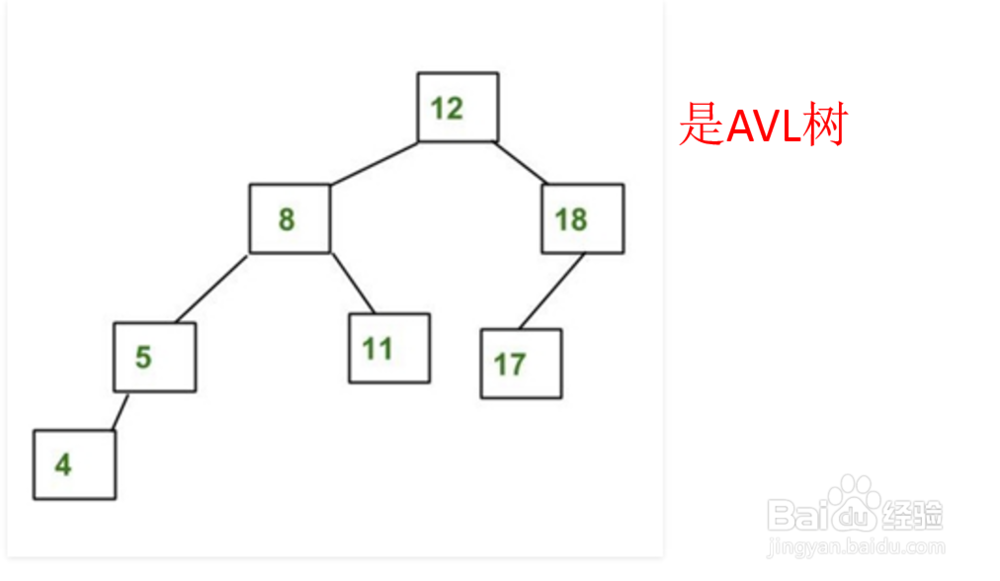
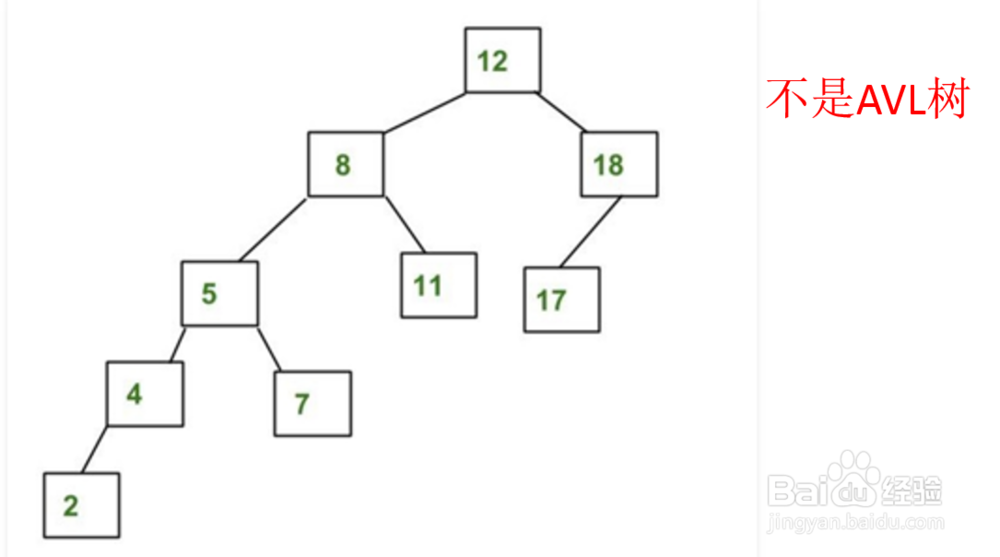
2、AVL树是通过旋转的操作实现二叉搜索树的平衡。下面对二叉搜索树的四种情况,介绍旋转操作。
1、left-left 情况
使用右旋转实现平衡。
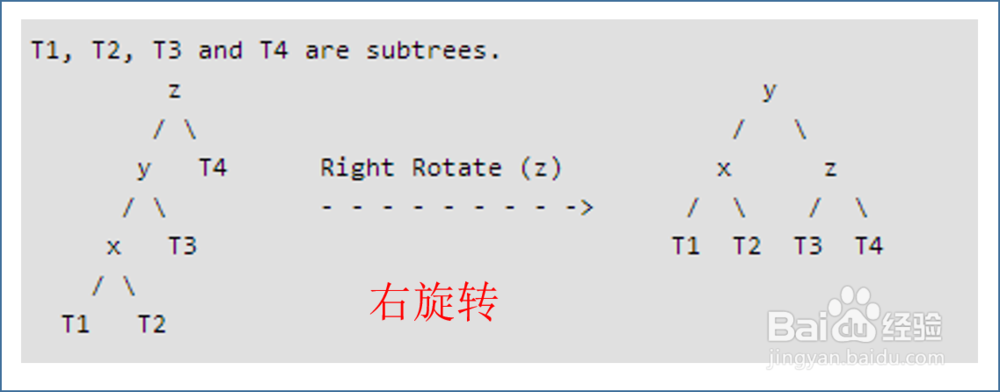
3、left-right 情况
这种情况下不平衡的二叉搜索树需要通过量子旋转进行平衡:先左旋转后右旋转。

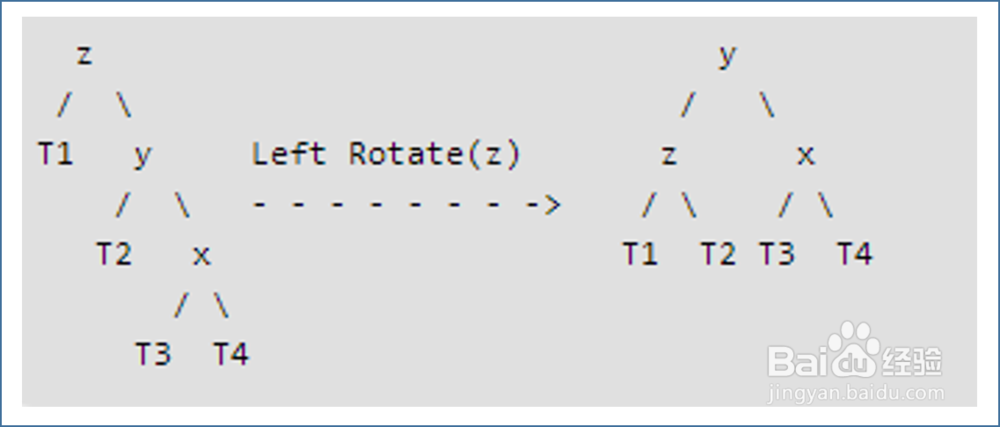
4、right-right 情况
这种情况需要一次旋转进行平衡,左旋转即可。
5、right-left 情况
需要先进行右旋转,再次进行左旋转即可实现树的平衡

6、在二叉搜索树插入操作的基础上,加入单旋转和双旋转的操作即可实现AVL树的插入操作。具体代码如下。
#include <iostream>
using namespace std;
//definite node
struct node
{
int key;
struct node*left;
struct node*right;
int hight;
};
//definite node hight
int hight(struct node*t)
{
if (t==nullptr)
return 0;
else return t->hight;
}
//construct new node
struct node* newnode(int item)
{
struct node* temp=new node;
temp->key=item;
temp->left=nullptr;
temp->right=nullptr;
temp->hight=1;
return temp;
};
int max(int a,int b)
{
if (a>b) return a;
else return b;
}
//single right rotate
// z y
// / \ / \
// y T4 Right Rotate (z) x z
// / \ - - - - - - - - -> / \ / \
// x T3 T1 T2 T3 T4
// / \
// T1 T2
struct node* RightRotate(struct node* z)
{
struct node*y=z->left;
struct node*T3=y->right;
z->left=T3;
y->right=z;
//update hight
z->hight=max(hight(T3),hight(z->left))+1;
y->hight=max(hight(z),hight(y->left))+1;
return y;
};
//single left rotate
// z y
// / \ / \
//T1 y Left Rotate(z) z x
// / \ - - - - - - - -> / \ / \
// T2 x T1 T2 T3 T4
// / \
// T3 T4
struct node*LeftRotate(struct node*z)
{
struct node*y=z->right;
struct node*T2=y->left;
y->left=z;
z->right=T2;
//update hight
z->hight=max(hight(z->left),hight(T2))+1;
y->hight=max(hight(z),hight(y->right))+1;
return y;
};
int getbalance(struct node* N)
{
if (N==nullptr)
return 0;
else return hight(N->left)-hight(N->right);
}
class AVLTree
{
public:
AVLTree(){root=nullptr;}
struct node*insert(struct node* t,int item)
{
//first step: perform normal BST insert
if (t==nullptr&&root==nullptr)
{
root=newnode(item);;
return root;
}
else if (t==nullptr&&root!=nullptr)
return newnode(item);
else if (item<t->key)
t->left=insert(t->left,item);
else if (item>t->key)
t->right=insert(t->right,item);
else return t;//equal key is not allowed in BST
root=t;
t->hight=1+max(hight(t->left),hight(t->right));//updata the hight
int balance=getbalance(t);
//there is 4 cases
//left-left case
if (balance>1&&item<t->left->key)
{
root=RightRotate(t);
return root;
}
//right-right case
if (balance<-1&&item>t->right->key)
{
root=LeftRotate(t);
return root;
}
//left-right case
if (balance>1&&item>t->left->key)
{
t->left=LeftRotate(t->left);
root=RightRotate(t);
return root;
}
if (balance<-1&&item<t->right->key)
{
t->right=RightRotate(t->right);
root=LeftRotate(t);
return root;
}
root=t;
return t;
};
struct node* root;
};
void preorder(struct node* t)
{
if (t!=nullptr)
{
cout<<t->key<<endl;
preorder(t->left);
preorder(t->right);
}
}
int main()
{
AVLTree tr;
tr.insert(tr.root,10);
tr.insert(tr.root,20);
tr.insert(tr.root,30);
tr.insert(tr.root,40);
tr.insert(tr.root,50);
tr.insert(tr.root,25);
tr.insert(tr.root,35);
tr.insert(tr.root,5);
preorder(tr.root);
cout<<tr.root->right->key;
return 0;
}