MATLAB如何实现一维/二维插值拉和格朗日插值？

1、第一步：数据插值的scope

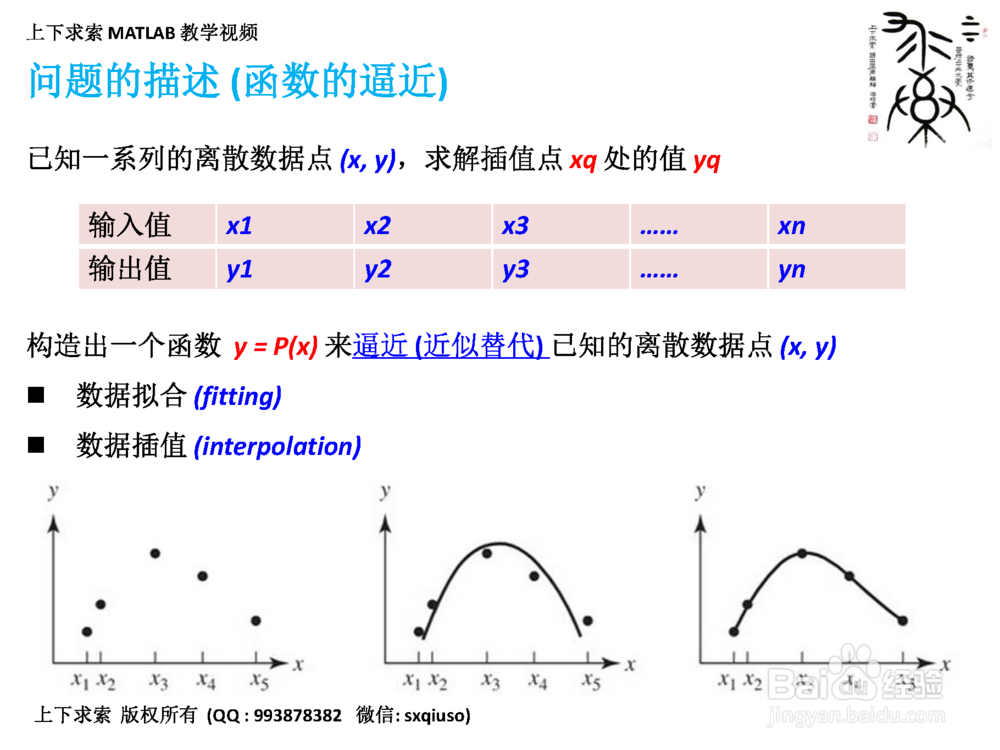
2、第二步：选择数据处理方法：什么是插值，什么是拟合？

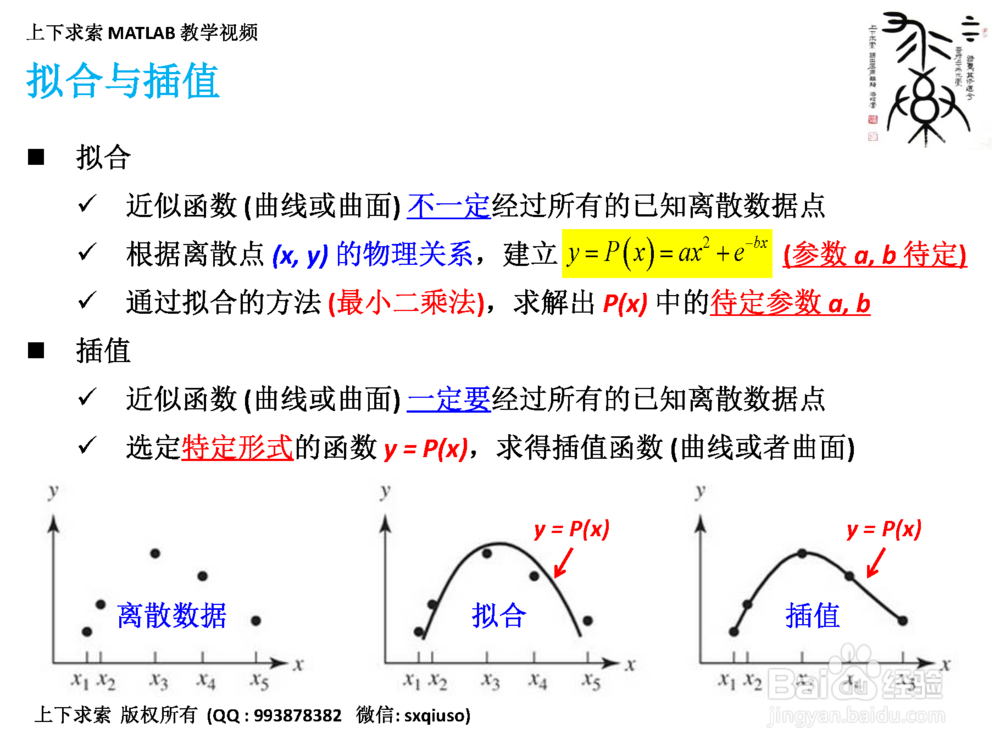
拟合

1. 近似函数(曲线或曲面) 不一定经过所有的已知离散数据点

2. 通过拟合的方法(最小二乘法)，求解出P(x)中的待定参数a, b

插值

1. 近似函数(曲线或曲面) 一定要经过所有的已知离散数据点

2. 选定特定形式的函数y = P(x)，求得插值函数(曲线或者曲面)

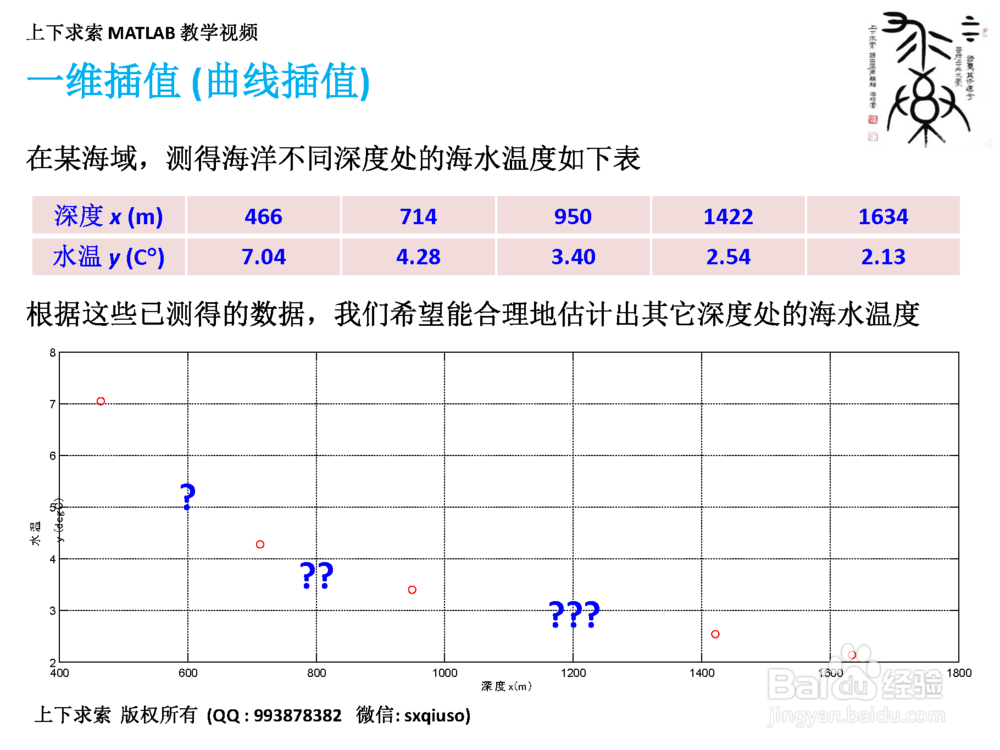
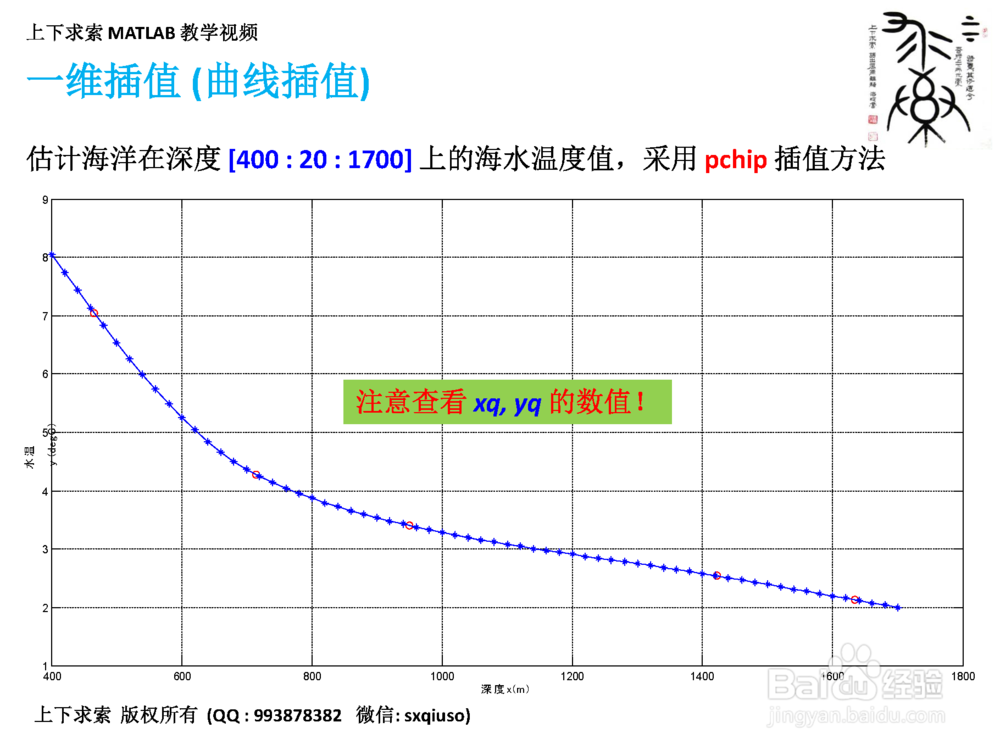
3、第三步：一维插值 （曲线插值）的执行，采用 MATLAB 的 interp1 函数

yq= interp1(x, y, xq, method)

method为可选用的插值方法

1. linear (线性插值，默认的插值方法)

2. nearest (最邻近插值)

3. spline(三次样条插值)

4. pchip(三次Hermite插值)

5. cubic (同pchip)

6. v5cubic (离散数据点必须是等间隔的)

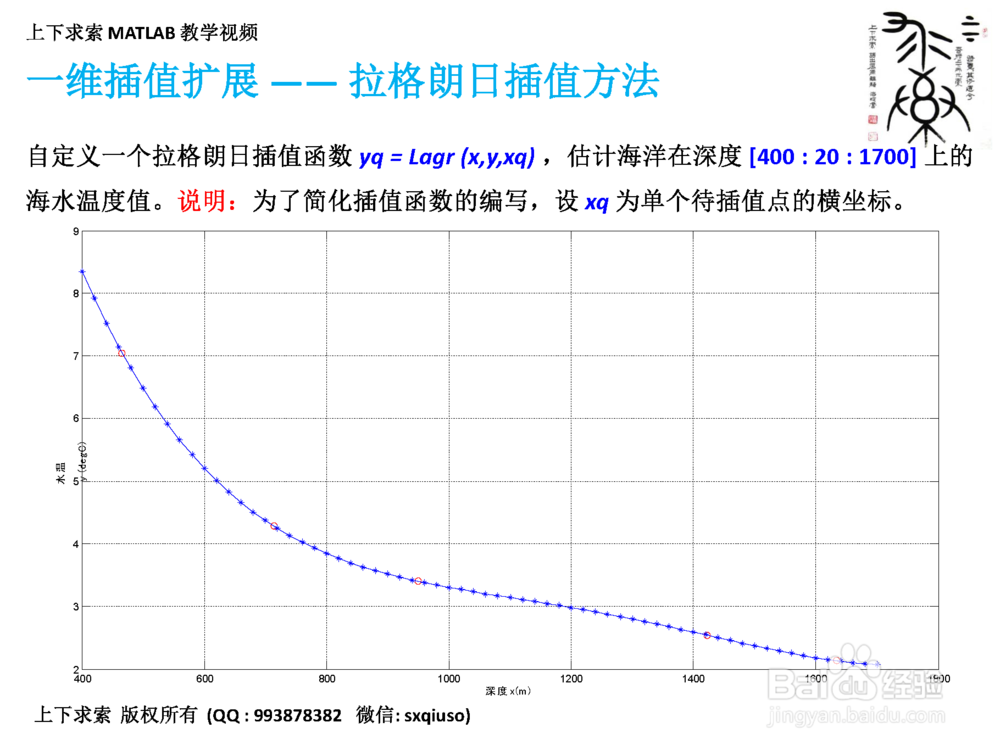
4、第四步：一维插值扩展——拉格朗日插值方法

拉格朗日插值是一种经典的多项式插值方法，可惜的是，MATLAB中并没有现成的内置函数，可以实现拉格朗日插值。这里直接给出拉格朗日插值多项式，具体的推导过程，可参照数值计算的教科书。

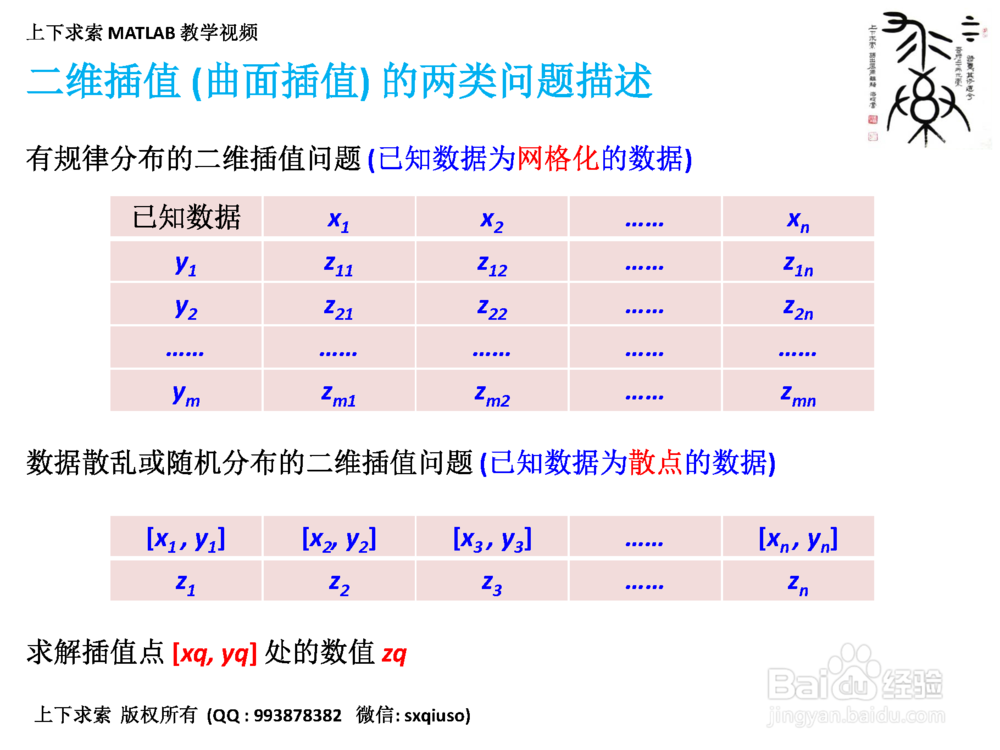
5、第五步：二维插值 （曲面插值）的两类问题描述，先要分清楚你的问题属于哪一类

已知数据为网格化的数据

zq= interp2(x, y, z, xq, yq, method)

已知数据为散点的数据

zq= griddata(x, y, z, xq, yq, method)

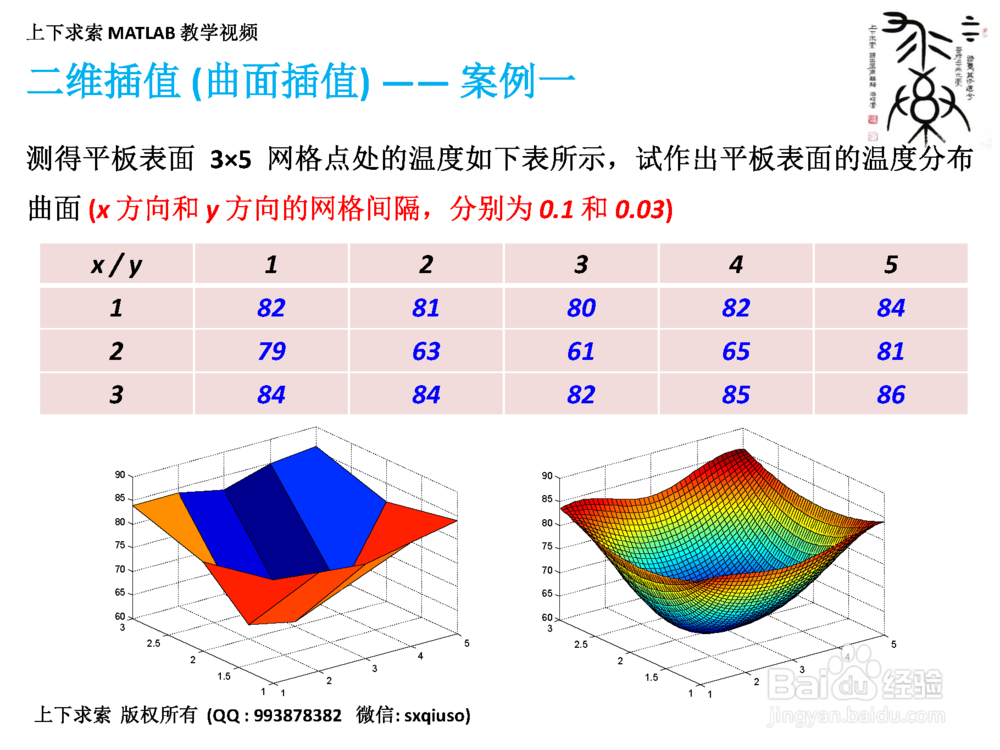
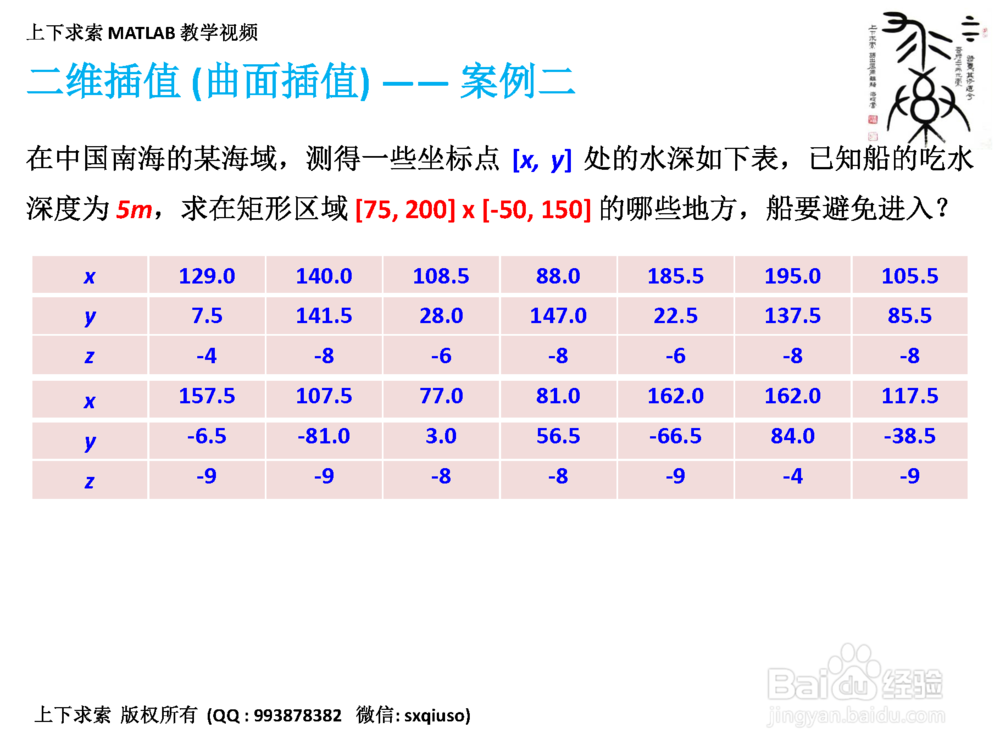
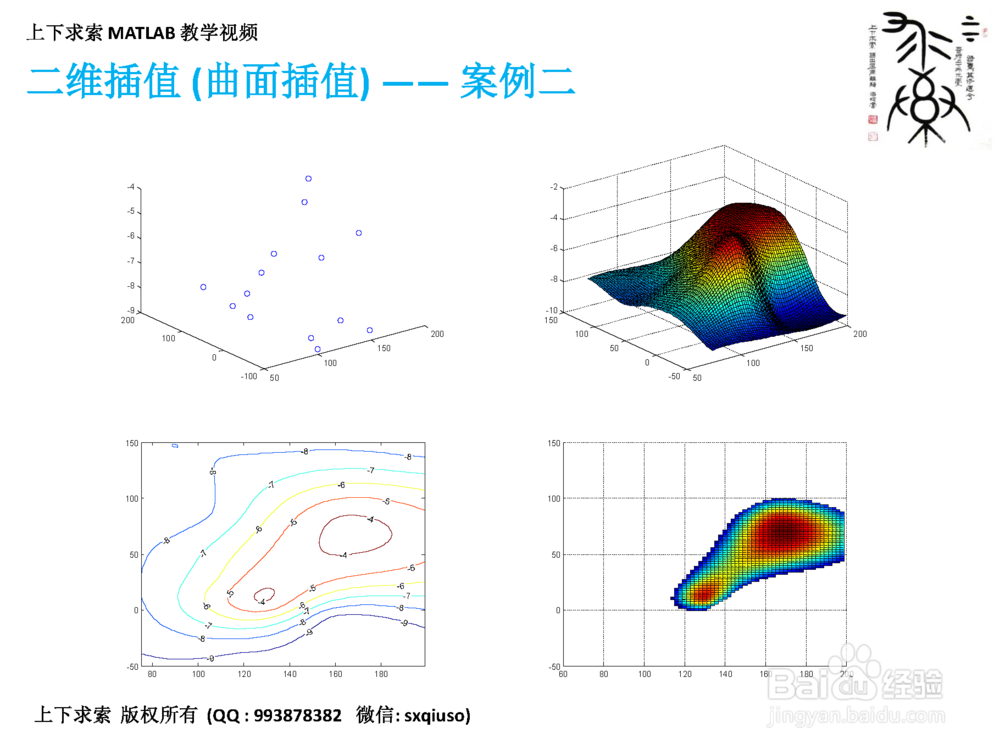
6、第六步：执行二维插值（曲面插值）

分别对网格化的数据和散点数据，使用 interp2 和 griddata 进行二维插值

7、第七步：多维插值的实现

已知数据为网格化的数据

Vq= interpn(X1, X2, ... , Xn, V, Xq1, Xq2, ... , Xqn, method)

已知数据为散点的数据

yi= griddatan(x, y, xi, method)